|
|
6ème collège |
|
|
|
||
|
|
||
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
1°)Informations
sur les calculs des volumes des prismes droits. a)
parallélisme. |
||
|
|
|
|
|
DOSSIER : LE PARALLELLEPIPEDE RECTANGLE .
Ou : Le prisme rectangulaire ou
« pavé » droit.
|
|
1°) Le cube. |
|
|
|
Exemple de dessin de patrons de cube ;
Fabrication de cubes ; Description du cube. Comparaisons des trois
cubes. |
|
|
|
2°) Patrons de cube. |
|
|
|
3° ) Le parallélépipède rectangle. |
|
|
|
Dessin
de patrons de parallélépipède rectangle. ; Fabrication de parallélépipède rectangle. ;
Description d’un parallélépipède rectangle |
|
|
|
|
|
|
TEST |
COURS |
Autres
travaux |
|
||||
|
|
|
|
Travaux niv
VI et V: |
Autres travaux : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
COURS |
|
|
|
|
1°) Le cube. |
|
|
|
|
Retrouvez autour de vous des exemples de
« cube » : Nous allons apprendre à en fabriquer quelques
un……….. |
|
|
|
|
a)
Dessin
de patrons de cube. |
|
|
|
|
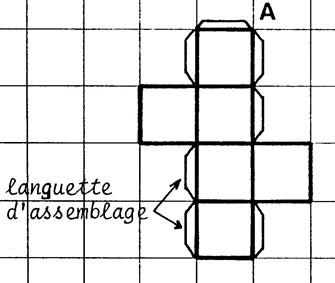
Ci-contre on vous a représenté le patron d’un
cube. On vous demande d’en faire deux agrandissements
sur feuille « A3 ». · L’un a l’échelle « 2 » . · L’autre à l’échelle « 6 » . Si vous le pouvez utiliser la page : Activité
1 |
|
|
|
|
|
Attention !!!!, n’oubliez pas de dessiner des
languettes d’assemblage. |
|
|
|
Attention !!!!, n’oubliez pas de dessiner des
languettes d’assemblage. |
|
|
|
|
Activité
1 : cliquez ici : pour obtenir la
feuille de tracé du cube ,…… on a placé le point « A » en bas à gauche pour l’échelle
« 2 » |
|
|
|
|
|
|
b)
Fabrication de cube :Découpez les « 3 » patrons ci-dessus, puis
collé convenablement les languettes ( avec du papier adhésif). Précaution : faites en sorte que le quadrillage
soit apparent. Vous avez obtenu trois cubes. |
|
|||
|
|
|
|
|||
|
|
c)
Description du
cube. |
|
|
||
|
|
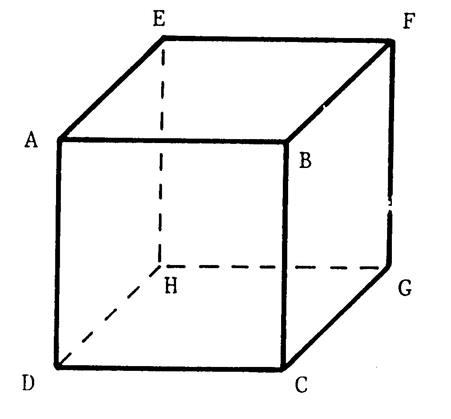
Considérons les cubes que vous venez de fabriquer
et les dessin ci-contre représentant un cube.. v E ; B ; H ; (par exemple)
sont des sommets . Activité 2 : v Nommez tous les sommets :………………………………………. v Combien en trouvez-vous ?.......................... v Les segments [ AB
], [ GH ],( par exemple)sont des arêtes.. Activité 3 : v Nommez tous les côtés. :…… …………………………………………………………………….. ; v Combien en trouvez -vous ? ………………………………. |
|
|
||
|
|
v Les surfaces telles que « ABCD »
sont appelées les »faces »
du cube. Activité 4 : v Que pouvez- vous dire quand à la forme de ces
surfaces ? ……………………………………………………………… v Nommez toutes les faces :
……… …………………………………………. v Combien en trouvez-vous ? ……. … ………………………… |
|
|||
|
|
|
|
|||
|
|
d)
Comparaisons des trois cubes. |
|
|||
|
|
|
|
|||
|
|
v Longueur des arêtes : -
La longueur de l’arête du grand cube est : ………………………………….. -
« ………… » fois plus
grande que celle du cube moyen … -
« …………. » fois plus
grande que celle du petit cube. |
|
|||
|
|
v Aires des faces : |
|
|||
|
|
-
L’aire d’une face du grand cube est :…………………………… -
« … …….»… fois plus grande que celle du cube moyen … -
« ……… » fois plus
grande que celle du petit cube. |
|
|||
|
|
v Volumes des solides : |
|
|||
|
|
-
Le volume du grand cube
est :…………………………… -
« … …….»… fois plus grand que celle du cube moyen … -
« ……… » fois plus
grand que celle du petit cube. |
|
|||
|
|
Si vous n’en êtes pas convaincu, comptez combien
vous pouvez placer de cubes moyens et de petits cubes dans le grand. |
|
|||
|
|
|
|
|||
|
|
2°) Patrons de cube. |
|
|||
|
|
Activité 5 : |
|
|||
|
|
En utilisant le quadrillage, vous allez dessiner
des patrons de cube. Essayez de trouver tous les cas possibles ( à savoir : différents ). Ne représentez qu’une seule fois ceux qui sont superposables . ( Des figures
superposables le sont par
demi-tour , par retournement , etc. ..) . |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
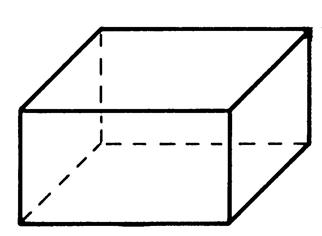
3° ) Le parallélépipède rectangle. |
|
|||
|
|
|
|
|||
|
|
a) Dessin de patrons de parallélépipède rectangle. |
|
|||
|
|
|
|
|||
|
|
· Activité 6 :Cliquez ici : page réservée à
l’activité de tracé |
|
|||
|
|
Complétez le dessin de telle sorte que la figure
soit symétrique par rapport à la droite « delta » : Δ |
|
|||
|
|
·
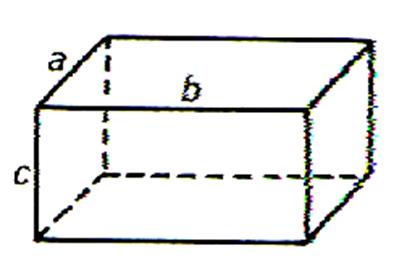
Activité 4 :Sur une feuille cartonnée libre , vous allez
dessiner le patron d’un
parallélépipède rectangle dont les dimensions
sont : 4,3 cm ; 6,5
cm et 8,5 cm. (
n’oubliez pas les languettes) |
|
|||
|
|
|
|
|||
|
|
b) Fabrication de parallélépipède rectangle. |
|
|||
|
|
Activité 5 :
Découpez les patrons des pages « activité 3 » et « activité 4 » . Puis collez convenablement les languettes avec
du papier adhésif…. Pour le parallélépipède
« activité 3 » faites en sorte que le quadrillage soit
apparent… Dans la vie courante,
vous rencontrez souvent de tels solide , donnez des
exemples : ……………….( Pensez à votre
chambre …) |
|
|||
|
|
|
|
|||
|
|
c)
Description d’un parallélépipède rectangle. |
|
|||
|
|
· Combien un tel solide a-t-il de
sommets ? ………….. · Combien un tel solide a-t-il d’ arêtes ? …… …….. · Combien un tel solide a-t-il de faces ? ……………. · Que peut-on dire de la forme de ces
faces : …………….…. · Un cube est-il un parallélépipède
rectangle ? … …. · Expliquez pourquoi ………… |
|
|
||
|
|
|
|
|||
|
|
Remarque : Un parallélépipède rectangle est
parfois appelé « pavé droit ». |
|
|||
|
|
|
|
|||
|
|
Activité 6 : |
|
|||
|
|
Calculez l’aire de la surface de chaque
parallélépipède que vous venez de fabriquer . ( rappel : on vous demande de calculer l’aire
de la surface du patron , sans les languettes ) ; |
|
|||
|
|
|
|
|||
|
|
|
|
|||
TRAVAUX AUTO
FORMATIFS.
Remplir la fiche !!!
Puis préparer le
CONTROLE :
Donner la définition d’un parallélépipède rectangle
.
EVALUATION
1°) Faire une représentation graphique ( dessiner)
un parallélépipède rectangle en perspective cavalière .
2°)
|
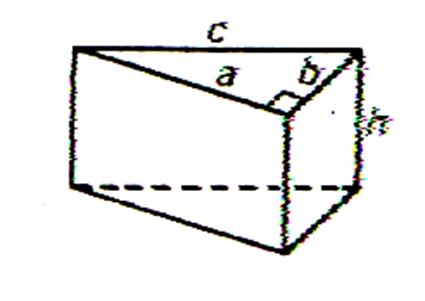
Calculer : - la longueur d’une diagonale - l’aire de la surface latérale - l’aire totale - le volume du parallélépipède droit avec les données suivantes : a = b = c = |
|
3°)
|
Calculer : - la longueur d’une diagonale - l’aire de la surface latérale - l’aire totale - le volume du parallélépipède droit avec les données suivantes : a = b = c = h = |
|
INTERDISCIPLINARITE : voir : dossier 219