Pré requis:
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
AVANT : :
1°) les parallélépipèdes rectangles. 2°) axiomes : point droite plan. |
APRES :
|
Complément d’Info :
Sommaire : Géométrie dans l’espace |
I ) Orthogonalité
de deux droites
II) Orthogonalité
de
droites et de plans
Travaux ; devoirs
|
|
Corrigé
|
|||
|
|
Contrôle |
évaluation |
|||
|
Interdisciplinarités : (matière concernée) |
||||||||
|
F |
H |
Géo. |
Vie
quotidienne et vie
familiale |
Autres : |
Sciences
et technique |
Physique Chimie Electricité |
Statistique. |
|
COURS
I ) Orthogonalité de deux droites
1°)Définition
Sur l’ensemble des droites de l’espace , on définit une
relation appelée orthogonalité , notée ^ et possédant
les propriétés suivantes :
|
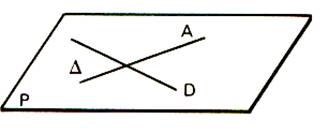
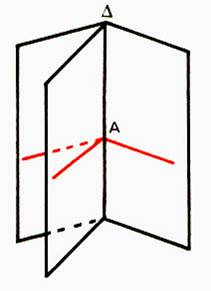
Quels que soient la droite
D et le point A non situé sur
« D » , il existe dans le plan défini par « A » et
« D » une droite D
et une seule contenant le point « A » et elle est dite « orthogonale » à la droite
« D » . |
|
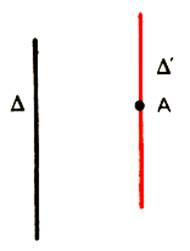
b) propriété 2 :
|
Si deux droites D et D sont coplanaires et si D est orthogonale à D , alors D et D sont sécantes
et D est orthogonales à D
. |
|
c) Propriété 3
|
Si une droite est
orthogonale à la droite D1 est parallèle à la
droite D2 alors la droite D est orthogonale à la
droite D2 . |
|
Remarque : deux droites orthogonales coplanaires
sont dites perpendiculaires.
2°) Propriétés .
a) Droites d’un plan
orthogonales à une même droite de ce plan.
|
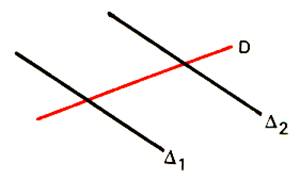
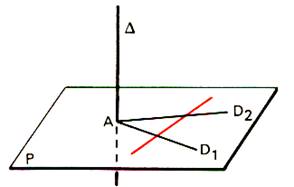
Soit deux droites D1
et D2 du plan orthogonales à la droite D de
P ; montrons que D1 et D2 sont parallèles. Si l’on avait D1
et D2 sécantes en A , il existerait deux droites
orthogonales à D et contenant le point A , ce qui est contraire à la
propriété 1. |
|
On énonce : Dans tout plan , deux droites orthogonales à
une même droite de ce plan sont
parallèles .
b)
Droites contenant un point et orthogonales à une droite donnée.
Soit une droite D et un point A
.
|
b1) Si A
appartient à D
, dans tout plan contenant D
, il existe une droite et une seule orthogonale à D et contenant A . Comme il y a une infinité de
plans contenant D
, il y a une infinité de droites orthogonales à D et contenant A . |
|
|
b2) Si A
n’appartient pas à D
, on considère la droite D’
contenant A et parallèle à D
. Toute droite orthogonale à D’ est orthogonale à D. On est alors ramené au problème précédent. |
|
On énonce : Il existe une infinité de droites orthogonales à une droite données et
contenant un point donné .
II) Orthogonalité de droites et de
plans
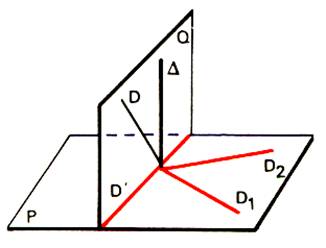
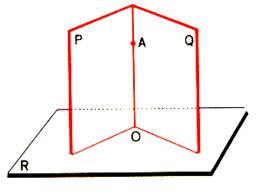
3°) Droites
orthogonales à une droite D en un point A
de D
Considérons deux telles
droites D1 et D2 . Elles définissent un plan P.
|
On démontre et on
admettra que la droite D est
orthogonale à toutes les droites du plan P. |
|
Conséquence :
|
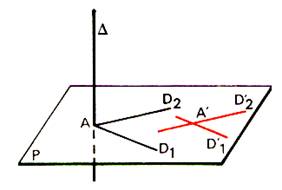
Soit une droite D rencontrant un plan P en A et orthogonale à deux
droites D’1 et D’2
du plan P sécantes en A’. La droite D est orthogonale aux droites D1 et D2
parallèles respectivement à D’1 et D’2 et contenant
A ; elle est donc orthogonale à toute droite du plan P |
|
On énonce : Si une
droite est orthogonale à deux droites sécantes d’un plan, elle est orthogonale
à toutes les droites de ce plan .
b) précisons ces droites :
|
Supposons qu’il existe une
droite D contenant un point A, orthogonale à D et non situé dans le plan P. Les droites D et D définissent un plan « Q » qui coupe le
plan P suivant une droite D’ contenant A. Or D’ est orthogonale à D. Dans le plan Q il
existerait alors deux droites distinctes D et D’ orthogonales à D et contenant
A, ce qui est impossible. |
|
On en déduit : L’ensemble des droites orthogonales à la
droite D et
contenant le point A de D est
l’ensemble des droites du plan P (
défini par D1 , et D2) contenant A.
c) définition . Une droite est dite
« orthogonale » (ou perpendiculaire) à un plan si elle est
orthogonale à tous les points de ce plan.
Les résultats précédents
permettent d’énoncer :
Une droite est orthogonale à un plan
si et seulement si elle est orthogonale
à deux droites sécantes de ce plan.
Le plan et la droite sont dits « perpendiculaires »
4°) Propriétés :
On démontre et on
admettra les résultats suivants :
|
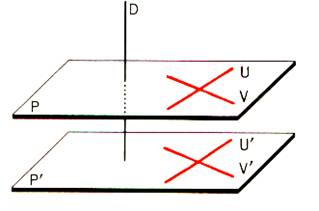
d1°) si deux plans sont parallèles,
toute droite perpendiculaire à l’un est perpendiculaire à l’autre. La droite D est
perpendiculaire à la direction de plans représentée par P. |
|
d2°)Si deux droites sont
parallèles , tout plan perpendiculaire à l’une est perpendiculaire à l’autre.
le plan est dit
perpendiculaire à la direction représentée par l’une des droites .
5°) Problème :
Etude d’une droite
orthogonale à un plan P et un point O
(contenu ou pas)
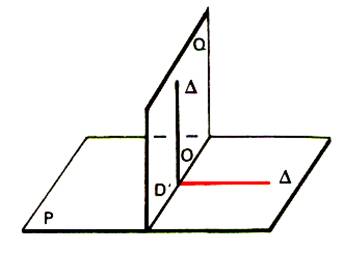
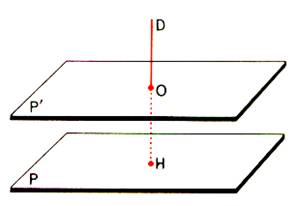
a) le point O appartient au plan P
|
Soit dans le plan
« P » une droite « D » contenant le point O puis le plan
« Q » perpendiculaire à « D » et contenant
« O ». Le plan Q est distinct du
plan P et coupe P suivant une droite D’ contenant O. Soit dans Q
la droite D
orthogonale à D’ et contenant le point O . La droite D étant orthogonale aux deux droites sécantes D et
D’ du plan P est perpendiculaire au plan P. |
|
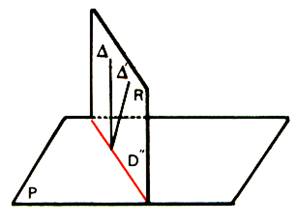
Cette droite D est unique .
|
En effet , s’il existe une
autre droite D’
perpendiculaire en O au plan P , celle-ci détermine avec D un plan R qui
coupe le plan P suivant une droite D’’. Cette droite D’’ du plan R est alors
perpendiculaire aux deux droites D et D’ concourantes de R , ce qui est impossible . |
|
b) le point O n’appartient pas au plan P.
|
Il suffit de considérer le
plan P’ , parallèle au plan P et contenant le point O. |
|
Théorème : Il
existe une droite et une seule perpendiculaire à un plan donné et contenant un
point donné.
6°) Problème
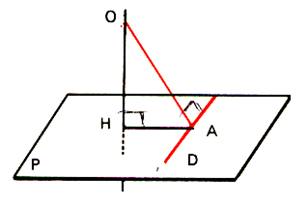
Théorème des trois perpendiculaires
|
Si la droite (OA) est orthogonale à une droite D du plan
P ( A appartenant à D ; O
n’appartenant pas à P ) et si la
droite ( OH) est orthogonale à P ( H appartenant à P) alors la droite ( AH)
est orthogonale à la droite D. |
|
Explication :
soit le plan P contenant une droite D et un point O n’appartenant pas à P .
Soit la droite ( OH) perpendiculaire au plan P et la droite ( OA)
perpendiculaire à la droite D . La droite D perpendiculaire à (
OA) et orthogonale à ( OH) est perpendiculaire au plan défini par les droites
(OA) et (OH) donc perpendiculaire à la
droite ( AH) de ce plan.
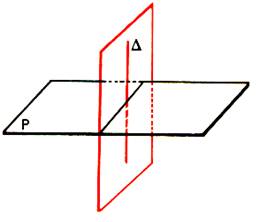
III Plans perpendiculaires. ( info rappel)
On note : P
^ Q et on lit
« P perpendiculaire à Q »
|
Définition : Un
plan Q est dit perpendiculaire à un plan P , s’il contient une droite D orthogonale au
plan P . |
|
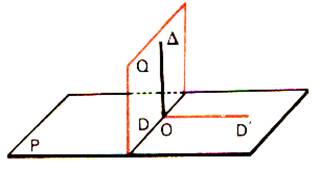
8°) Propriété
Démontrons que si le plan
Q est perpendiculaire au plan P , alors le
plan P est perpendiculaire au plan Q.
|
La droite D de Q orthogonale à P coupe le plan P au point O et le plan Q coupe le plan P suivant une droite D contenant O
. |
|
Considérons la droite D’ du
plan P contenant O et orthogonale à D . La droite D orthogonale à P est orthogonale à la droite D’ de P
.
Ainsi : D’ ^ D et
D’^ D.
La droite D’ orthogonale à
deux droites sécantes de Q est donc orthogonale au plan Q.
On énoncera :
Le plan
P contenant la droite D’ orthogonale au plan Q est donc perpendiculaire au plan
Q .
Remarque : On pourra alors dire que les plans P et Q
sont perpendiculaires.
9°) Conséquence et application :
a) conséquence . On
a établi précédemment que la droite D’
incluse dans le plan Q et perpendiculaire à l’intersection D des plans P et Q
est perpendiculaire au plan Q.
On énoncera :
Si deux plans sont perpendiculaires, toute perpendiculaire à leur
intersection incluse dans un des plans est perpendiculaire à l’autre plan.
b)
Application .
|
Soit
deux plans P et Q perpendiculaires au plan R et un point A de l’intersection
des plans P et Q |
|
La droite D du
plan P qui contient A et qui est perpendiculaire à l’intersection des
plans « P » et « R »
est perpendiculaire au plan « R ».
(Conséquence « a ») .
De même, la droite D’ du
plan Q qui contient le point A et qui est perpendiculaire à l’intersection des
plans Q et R est perpendiculaire au plan
R.
Comme il
existe une seule droite contenant A et perpendiculaire à R , les droites D et D’ sont confondues ; il s’agit donc de
l’intersection des plans P et Q .
On
énonce :
Si
deux plans sécants sont perpendiculaires à un même troisième , leur intersection
est perpendiculaire à ce troisième plan .
1°)Trouver des exemples
concrets de droites perpendiculaires , de droite et plan perpendiculaire , de
plans perpendiculaires (orthogonaux )
1°) Droite et
perpendiculaires.
Une droite D est orthogonale
à deux droites D1 et D2
parallèles à un plan P mais non parallèles entre elles. Démontrer que D est perpendiculaire à P.
2°) Plans perpendiculaires.
Un plan
Q est perpendiculaire à une droite contenue dans un plan P . Démontrer que le
plan Q est perpendiculaire au plan P.