Pré requis:

Les lignes
Le segment.
POINT LIGNE PLAN

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent Cours : le polygone

Objectif suivant 1°) quadrilatères 2°) Tracés de polygones 3°) les polygones réguliers 4°) Les polygones irréguliers 5°) le périmètre d’un polygone irrégulier.

Liste des cours de géométrie. 1°) sommaire sur les polygones 2°) Info : Le périmètre des polygones 3°) Voir programme 6^ème collège

DOSSIER 1: Activités découverte .LE POLYGONE 

	1. Ligne polygonale
	2. Polygone.
	3. Les principaux polygones.
	4. Hexagone régulier et triangle équilatéral.
	5. Octogone régulier et « carré »
	6. Les quadrilatères particuliers.(parallélogramme ; Le trapèze. Losange ; Carré ; rectangle )
	7. Reconnaître des polygones
	8. Exercice de construction.
	9. Dessin . « géométrique »
TEST		COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité 1° les polyèdres	Corrigé Contrôle	Corrigé évaluation
					2°) l’arpentage.

COURS

1°) Ligne polygonale
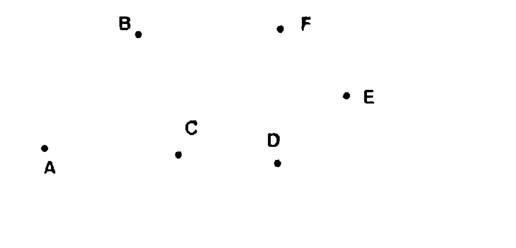
On vous donne plusieurs points dans un ordre déterminé : A.B.C.D.E.F. On vous demande de joindre par des segments ces points dans l’ordre donné. La figure obtenue s’appelle : « une ligne polygonale » . On la note « ABCDEF »
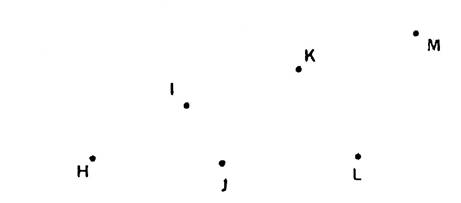
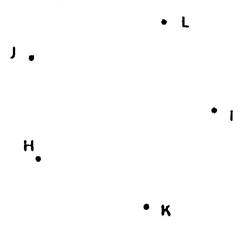
Faire de même pour « H,I,J,K,L,M »
2°) Polygone.
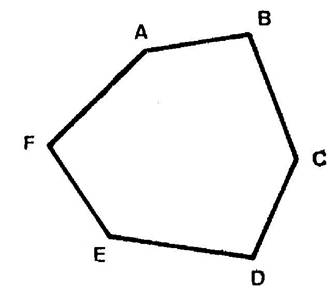
Ci contre vous observé un polygone dans lequel le dernier point coïncide avec le premier. On le note « ABCDEF ». On pourrait aussi le noter par exemple « EFABCD » . Activités : · Parmi les notations suivantes sont incorrectes :barrez les ! « CDEFABC » ; « FEDCBA » ; « ECAFBD »
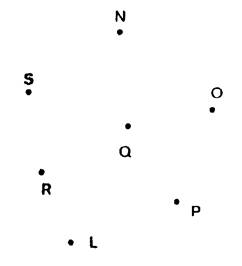
Tracer le polygone « SNOPQR » . ( n’oubliez pas de joindre le dernier point au premier !)
Tracer le polygone « HIJKL » .
Vocabulaire :
· Pour le polygone « ABCDEF » , les points A ;B ;C ;…… sont les sommets
· « A » et « B » sont des sommets consécutifs ; ainsi que « D » et « E »
Activités :
a) On vous demande de nommer d’autres sommets consécutifs.
b) On vous demande de nommer des sommets non- consécutifs.
· Les segments [ AB ] , [ BC ],………….., [ FA ] , joignant des sommets consécutifs, sont les « côtés »
· Les segments [ DB ] , [ BE ],………….., joignant des sommets non - consécutifs, sont les « diagonales »
Activités :
On vous demande de tracer toutes les diagonales du polygone « ABCDEF ».
Activités : Tracer le polygone.
Considérons le polygone : · Nommez ses sommets. · Nommez ses côtés. · Nommez les diagonales.
Info :
· Le polygone « ABCDEF » est dit convexe.
· Le polygone « SNOPQR » est dit « concave » ; il est « non convexe »
· Le polygone « HIJKL » est dit « étoilé » ; il est « non convexe »
4°) Les principaux polygones.
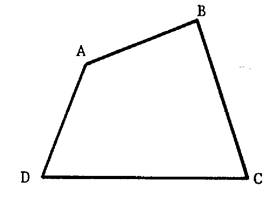
Un polygone ayant quatre côtés est un quadrilatère. Activité : Combien y a-t-il de diagonales ? ……………………(tracez –les ) Les segments [AB] et [ DC ] sont appelés « côtés opposés » : nommés les deux autres : ……………………….. Les segments [AB] et [ BC ] sont appelés « côtés consécutifs» : ainsi que ……………..et ………… ou …………..et ………………………….
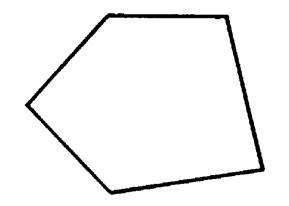
· Un polygone ayant 5 côtés est un pentagone : · Combien a – t- il de diagonales ? Tracez – les ………………………..
· Un polygone ayant 6 côtés est un hexagone : · Combien a – t- il de diagonales ?En déterminer le nombre par le calcul. ………………………..
· Un polygone ayant 8 côtés est un octogone : · Combien a – t- il de diagonales ? En déterminer le nombre par le calcul. ………………………..
4°) Hexagone régulier et triangle équilatéral.
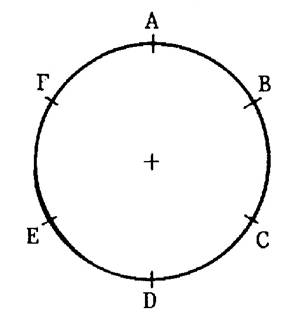
Un hexagone régulier a ses sommets situés sur un même cercle et la longueur de ses côtés est égale à la longueur du rayon du cercle. Activités :
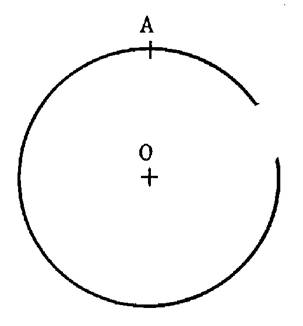
1 : 1 : Sur le cercle ci- dessous , est placé un point « A » . A l’aide d’un compas dont l’ouverture est égale à la longueur du rayon « OA », tracer la position des points B ;C ;D ;E ;F du polygone. Puis tracer les côtés de l’hexagone régulier « ABCDEF »				2 : Sur la figure ci-dessous on a placé les sommets d’un hexagone régulier. · Tracer de couleurs différentes les triangles « ACE » et « FBD » · Comment appelle-t-on de tels triangles ? Triangles équilatérales
voir des tracés : Les polygones réguliers
23_09_2012
5°) Octogone régulier et « carré »
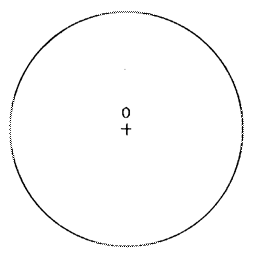
Un octogone régulier a ses sommets situés sur un même cercle et ses côtés ont tous la même longueur. Activité : Ci contre un cercle de centre « O ». On vous demande de : Tracer deux diamètres perpendiculaires. Tracer les bissectrices des quatre angles droits que vous avez déterminé précédemment.. Ces 8 demi – droites d’origine « O » coupent le cercle en 8 points que l’on nomme « A ,B , C , D , E, F, G,H » ; tracez les segments consécutifs. Le polygone « A ,B , C , D , E, F, G,H » est un « octogone régulier »
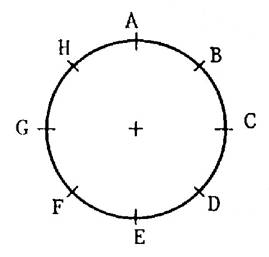
Sur les figures ci-dessous on a placé les sommets d’un octogone régulier.
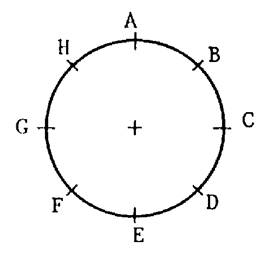
Figure 1 : Tracez les polygones « ACGE » et « BDFH » . Comment nomme t- on ces quadrilatères. ?				Figure 2 : Tracez le polygone « ADGBEHCF » , ne pas oublier le dernier côté. Comment nomme –t – on un tel polygone ?
6°) Les quadrilatères particuliers.
Le trapèze.
a) Le trapèze.
b) Le parallélogramme
Ses côtés opposés sont parallèles . Activités : · Dessiner ci contre le parallélogramme « ABCD » dont on donne trois sommets « A,B,C » · Comparer les longueurs des côtés opposés. Que peut –on en dire ? …………………………………………………….. …………………………………………………. info +++
c) Rectangle :
Ses côtés opposés sont parallèles et ses côtés consécutifs sont perpendiculaires. . Activités : · Dessinez le rectangle « EFGH » dont ion vous donne le côté [ E F ] et tel que « FG = 35 mm » · Dites en expliquant si un rectangle est un parallélogramme. · Tracer les diagonales ; comparer les longueurs de celles-ci . Que pouvez vous en dire ?
d) Losange :
Le losange :Ses côtés opposés sont parallèles. Et ses quatre côtés ont la même longueur . Activités : Dessinez ci contre le losange « KLMN », dont on donne deux sommets opposés «K » et « M » et dont les longueurs des côtés est de 40 mm. Dites , en expliquant si un losange est un parallélogramme : ……………………………………………………………………………………. Tracer les diagonales . Que pouvez vous en dire ? ………………………………………………………………………………….
e) Carré :
Ses côtés opposés sont parallèles. Ses côtés consécutifs sont perpendiculaires et ses quatre côtés ont la même longueur . Activités : · Dessinez le carré « PRST » dont on donne deux sommets consécutifs « P » et « R ». · Expliquez pourquoi un carré est un rectangle. · Expliquez pourquoi un carré est un losange. · Que peut-on dire de ses diagonales ? .
7°) Reconnaître des quadrilatères.
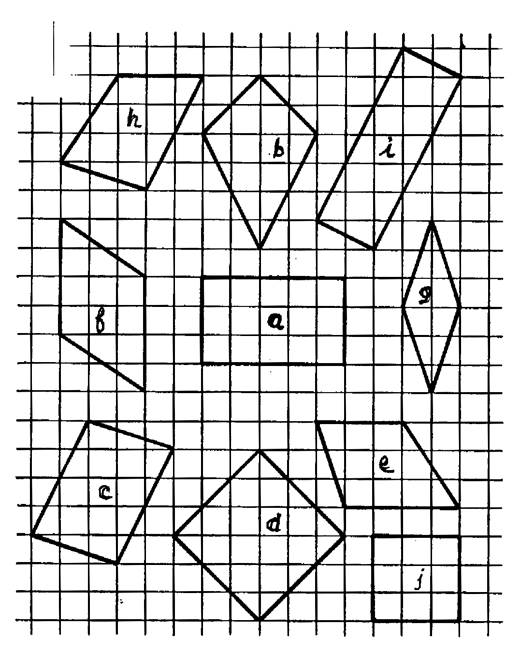
Activités 1 : On a dessiné ci-dessous des quadrilatères : a ;b ; c ; d ; ………………….Vous devez dire si se sont des carrés , rectangles , ……… Pour cela ,complétez le tableau en mettant une croix chaque fois que la réponse est « vraie ». (pour l’exemple : ) N’oubliez pas qu’un rectangle est un parallélogramme et que …………………
	a	b	c		d	e	f	g	h	i	j
Parallélogramme
Rectangle
Losange
Carré
Trapèze non parallélogramme
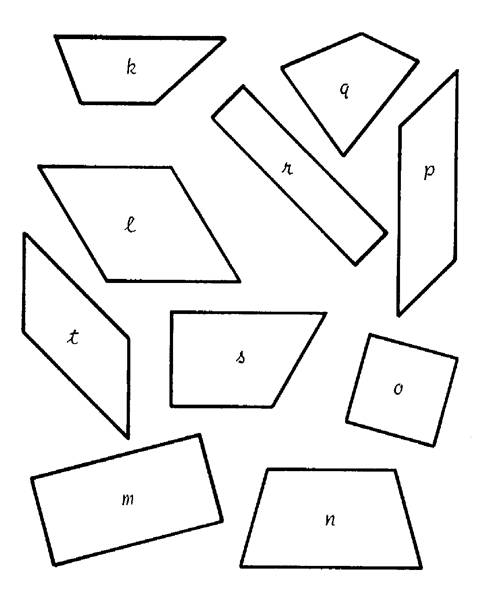
Activités 1 : On a dessiné ci-dessous des quadrilatères : a ;b ; c ; d ; ………………….Vous devez dire si se sont des carrés , rectangles , ……… Pour cela ,complétez le tableau en mettant une croix chaque fois que la réponse est « vraie ». (pour l’exemple : ) N’oubliez pas qu’un rectangle est un parallélogramme et que …
	k	l	m		n	o	p	q	r	s	t
Parallélogramme
Rectangle
Losange
Carré
Trapèze non parallélogramme
Remarque : un trapèze isocèle est un trapèze dont les côtés non parallèles ont la même longueur . Nommez celui ( ou ceux ) que vous avez trouvez . …………………………………………………………………………………..
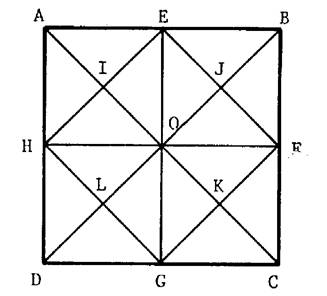
· Nommez les carrés de la figure ci contre. · Nommer tous les rectangles qui ne sont pas carrés.
8°) Exercice de construction.
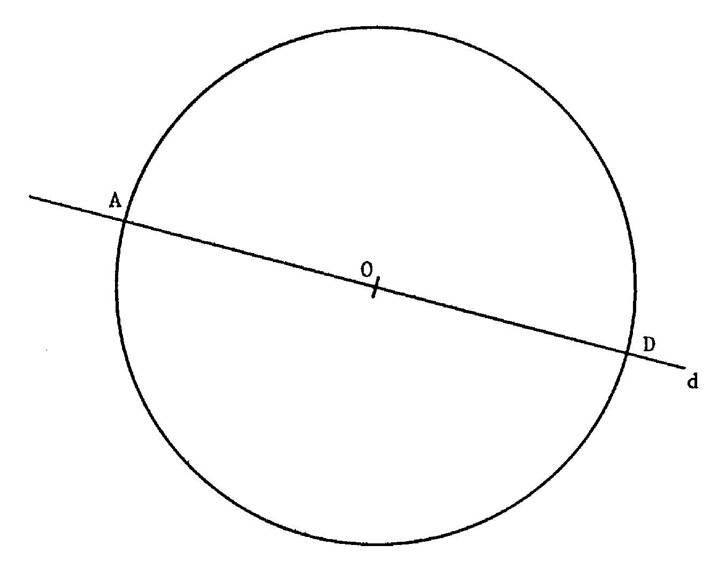
On donne un cercle « O » et une droite « d » passant par « O » qui coupe le cercle en « A » et « D ». · Par le milieu du segment [ OD ] tracez la perpendiculaire à « d ». Elle coupe le cercle en deux points : « C » et « E » . · Par le point « C » tracer la parallèle à « d » qui coupe le cercle au point « B ». · Par « E » tracez la parallèle à « d » qui coupe le cercle en un point « F ». · Tracer la droite ( A B ) ; puis ( A F ) , puis (D E ) et ( D C ) . · Tracer les droites ( B E ) et ( C F ) . · Si votre dessin est bien fait , les droites ( B E ) et ( C F ) doivent passer par « O ».. · Sinon : effacer et recommencer sur cette feuille ou une autre feuille . · Tracez les droites : ( B F ) ; puis ( A C ) , ( A E ) et ( B D ) .
Comment appelle – t- on un polygone tel que «  ABCDEF ». En utilisant uniquement le nom des points A , B , C , D , E , F , O . Nommer : 1° ) Les droites qui vous semblent ou qui sont parallèles. Exemple ( B C ) // ( A D ) // ( E F ) 2°) Les droites qui vous semblent ou qui sont perpendiculaires .Exemple : ( C E ) ( A D ) 3° ) Les triangles équilatéraux. 4°) Les triangles isocèles ( mais non équilatéraux ) . 5°) les triangles rectangles. 6°) Les rectangles 7°) Les losanges.
9°) Dessin :
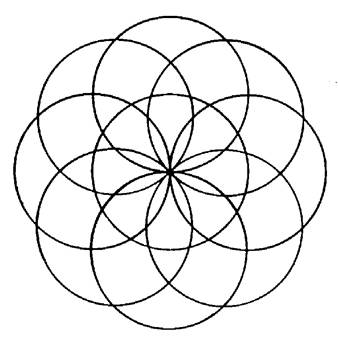
Vous allez reproduire le dessin ci contre et le colorier à votre goût. Procédure : Commencer par tracer un cercle au centre d’une feuille ( prendre un rayon de 40 mm) . C’est sur ce cercle que se trouvent les centres des autres cercles.. Combien faut-il de centre à déterminer . ? Faire les constructions qui s’imposent. Et placer les centres avec précision. !!!