Pré requis:
|
|
ENVIRONNEMENT du dossier:
AVANT : :
|
APRES :
|
Complément d’Info :
Sommaire : Géométrie dans l’espace |
TITRE
: Géométrie dans
l’espace : LE PARALLELISME
I )
DROITES PARALLELES : définition ;propriétés
II) DROITES ET PLANS
PARALLELES.
Travaux ; devoirs
|
|
Corrigé
|
|||
|
|
Contrôle |
évaluation |
|||
|
Interdisciplinarités : (matière concernée) |
|||||||||
|
F |
H |
Géo. |
Vie quotidienne et vie familiale |
Autres : |
Sciences et technique |
Physique Chimie Electricité |
Statistique. |
|
|
COURS
1°) DEFINITION
Deux droites
« D » et « D’ » de l’espace sont parallèles si et
seulement si :
a)
ou bien elles sont
confondues ;
b)
ou bien elles sont
coplanaires , distinctes et sans point commun.
On
écrit D // D’
|
Il
faut remarquer que dans
l’espace deux droites non parallèles ne sont pas nécessairement
concourantes puisqu’elles peuvent
être non coplanaires. Il
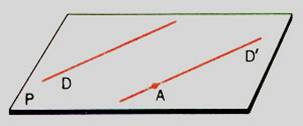
résulte de la définition que deux droites parallèles distinctes
« D » et « D’ » déterminent un plan : le plan défini par
« D » et un point
« A » appartenant à « D’ ». |
Soit une droite « D » et un point
« A » n’appartenant pas à « D » . Le point « A »
et la droite « D » déterminent un plan et un seul. Dans ce plan ,
d’après l’axiome d’ Euclide , il existe une droite « D’ » et
une seule contenant « A » et parallèle à « D » .
Donc :
Par un point extérieur à une
droite , on peut mener une parallèle et
une seule à cette droite .
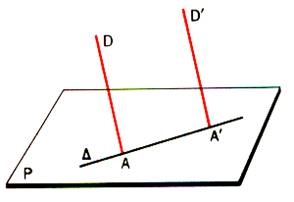
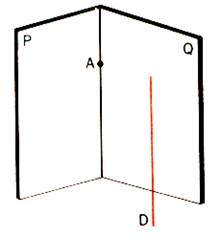
a) théorème . Si
deux droites sont parallèles , tout plan qui coupe l’une coupe l’autre .
|
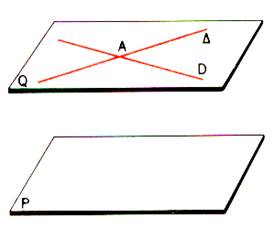
Soit « D » et « D’ » deux
droites parallèles distinctes définissant le plan « Q » et soit
« P » un plan qui coupe « D » en « A »
.L’ensemble des points communs à « P » et « Q » est
une droite D qui passe par A . |
|
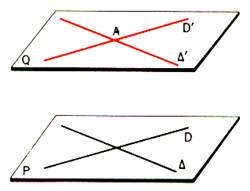
Dans le plan « Q » , la droite D coupe « D » ,
donc coupe sa parallèle « D’ » en un point « A’ » . Ce
point « A’ » est le seul point commun à « D’ » et à
« P » puisque « P » et « Q » n’ont pas de points
communs en dehors de ceux de D. Donc si « P »
coupe « D » , il coupe la parallèle « D’ » à
« D » au point « A’ ».
b)Relation de parallélisme .
La relation , définie dans l’ensemble des droites de l’espace « E » par
« est parallèle à » et appelée relation de parallélisme,
est :
Réflexive :
toute droite de l’espace est parallèle à lui-même ;
Symétrique :
si « D » est parallèle à
« D’ » , alors »D’ » est parallèle à « D » ;
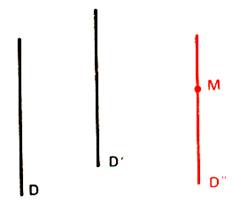
Transitive : nous
montrons en effet que si « D » est parallèle à
« D’ » et si « D’ » est parallèle à « D’ » ,
alors « D » est parallèle à « D’ ».
|
Soit le plan « P » déterminé
par « D » et un point « M » de « D’’ ». Si
D’’ n’est pas incluse dans P , P coupe D’’ en M , donc coupe D’
parallèle à D’’ et coupe D parallèle à D’ , il y a contradiction puisque D est
incluse dans P . Donc D’’ est incluse dans P . |
|
D et D’’ n’ont aucun point commun , car si elles en avaient un , on
pourrait mener par ce point deux parallèles distinctes à D’ ; donc :
D //D’’.
En conclusion , dans l’ensemble des droites de l’espace
E , la relation de parallélisme est une relation
d’équivalence.
.La classe d’équivalence d’une droite donnée D est l’ensemble des
droites de l’espace qui sont parallèles à D .
Définition : Toute classe d’équivalence est appelée
direction de droites.
II)
DROITES ET PLANS PARALLELES.
1°) THEOREME d’
EXISTENCE :
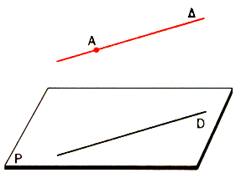
Soit le point A extérieur au plan P et la droite D parallèle à la
droite D de P et contenant le point A.
|
La droite D contenant A extérieur à P n’est pas incluse dans P ; si P
coupe D , il coupe alors sa parallèle D ; ceci
contredit l’hypothèse selon laquelle P contient D . |
|
Théorème : Etant donné un plan , il
existe des droites de l’espace n’ayant aucun point commun avec ce plan .
2°)DEFINITION :
Une droite D et un plan P sont parallèles si et
seulement si :
a)ou bien la droite D est incluse dans le plan P
b)ou bien la droite D et le plan P n’ont aucun point
commun.
Une droite et un plan parallèles n’ayant aucun point commun sont dits strictement parallèles.
3°)THEOREME.
Si une droite est parallèle à un plan ,
elle est parallèle à une droite de ce plan .
Si la
droite est incluse dans le plan , le résultat
est immédiat.
Si nous supposons la droite D non incluse dans P ; dans ce cas D et P n’ont aucun point
commun.
Soit Q le
plan déterminé par la droite D et
un point A du plan P . Q coupe P suivant une droite D . Les droites D et D sont dans un même plan Q
et ne peuvent se couper en un point C , sinon C appartiendrait à la
fois à D et
à P , ce qui contredirait l’hypothèse (D et P n’ont aucun point commun) .
4°)CONDITION DE PARALLELISME.
En tenant compte des
résultats précédents , on déduit :
Une droite est parallèle à un plan si et seulement si elle est parallèle
à une droite de ce plan.
5°) CONSEQUENCES .
a)
Si une droite D et un plan
P sont parallèles , toute parallèle D à D est parallèle à P .
En effet , étant donné deux parallèles D et D , un plan qui ne coupe pas
l’une ne coupe pas l’autre .
b)
Si une droite
D et un plan P sont parallèles , la parallèle à D menée par un point de
P est incluse dans P .
6°) PLANS SECANTS PARALLELES A UNE DROITE.
Soit deux plans sécants P et Q parallèles à la droite D et soit un point A
commun aux deux plans .
|
La parallèle à D menée par A est incluse dans chaque
plan ; c’est donc leur intersection. (voir : conséquence b ) |
|
Théorème :
Si une droite est parallèle à deux
plans sécants , elle est parallèle à
leur intersection .
En particulier , si une droite « D » et un plan
« P » sont parallèles , tout plan qui contient D et qui coupe P , le
coupe suivant une droite parallèle à D .
1°)
EXISTENCE ET DEFINITION.
a) Existence : Soit un plan P et un point A extérieur
à P .
|
Par A menons deux droites D et D parallèles à P . Elles
déterminent un plan Q distinct de P
car A n’appartient pas à P . Si Q coupait P , la droite d’intersection incluse
dans P serait à la fois parallèle aux deux droites sécantes D et D (
6° ci dessus) , ce qui serait impossible . |
|
b) Définition.
Deux plans « P » et « Q » sont
parallèles si et seulement si :
a)
ou bien ils sont confondus.
b)
Ou bien il n’ont aucun
point commun.
On écrit P
//Q
Si « P » et « Q » n’ont aucun
point commun , on dit qu’ils sont strictement
parallèles.
3°) Propriétés .
a) la démonstration
d’existence conduit au théorème suivant :
Si deux droites sécantes d’un plan
« Q » sont parallèles à un plan « P » ; les plans P et
Q sont parallèles.
b) d’après la définition , il va de soit que :
Si deux plans sont parallèles , toute
droite incluse dans l’un est parallèle à l’autre .
Des deux propositions précédentes, il en résulte que :
Deux plans sont parallèles si et seulement
si deux droites sécantes de l’un sont parallèles à l’autre .
4°)
Plan passant par un point et parallèle à un plan .
|
Pour mener par un point « A » un plan
« Q » parallèle à un plan « P », il suffit de construire
les droites « D’ » et D’
passant par « A » et respectivement parallèles aux droites
concourantes D et D
du plan P . |
|
Ce plan « Q » est unique : s’il
existait un second plan Q’ , ce plan Q’
contiendrait D’ car s’il la coupait en A , il couperait aussi sa parallèle D ,
donc il couperait le plan P . De même Q’ contient D’ . Il est donc confondu
avec P’ .
On énoncera le théorème suivant :
Il existe un plan et un seul parallèle à un
plan donné et passant par un point donné
.
5°)Relation
de parallélisme dans l’ensemble des plans de l’espace.
la relation définie dans l’ensemble des plans de
l’espace E par « est parallèle à »
et appelé « relation de parallélisme » est :
réflexive : tout plan de l’espace est parallèle à lui-même.
Symétrique : si P est parallèle à P’ , alors P’
est parallèle à P .
Transitive : nous pouvons montrer que si P est
parallèle à P’ et si P’ est parallèle à P’’ , alors P est parallèle à P’’ .
Si P et P’ sont confondus , alors ils sont
parallèles.
Si P et P’’ sont distincts , ils n’ont aucun point
commun. En effet , s’ils avaient un point commun A , il passerait par A deux
plans distincts parallèles à P’, ce qui est impossible. ( voir précédent 4°) : plan passant par un
point …..)
La relation de parallélisme dans l’ensemble des
droites de l’espace est donc une relation
d’équivalence .
A
retenir : La classe d’équivalence du plan P , ensemble des plans
parallèles à P , est appelée « direction »
du plan.
5°)
Problème :
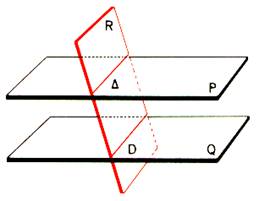
a) Trois plans : on veut étudier la figure
formée par deux plans parallèles et distincts de P et Q et un plan R qui coupe
P.
|
Si R est parallèle à Q , les plans P et R
distincts et parallèles à Q seraient parallèles , ce qui n’est pas le cas
puisque R coupe P .(voir ci contre) Donc Q et
R sont sécants . Les intersections D
et D de R avec P et Q sont des
droites coplanaires et sans point
commun puisque situés dans deux plans parallèles distincts P et Q . |
|
D’où le théorème suivant :
Si deux
plans sont parallèles , tout plan qui coupe l’un coupe l’autre et les droites
d’intersection sont parallèles.
|
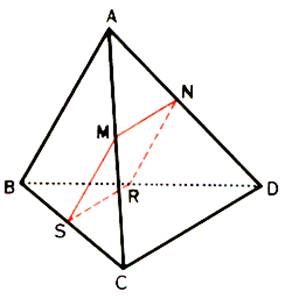
Tétraèdre :
On donne un tétraèdre ABCD . Par un point M de l’arête [AC] on fait passer un
plan P parallèle aux droites (AB) et ( CD), déterminé en menant par M les
parallèles à ces droites. Etude de la section par ce plan: Le plan P et le plan de la face ACD sont
parallèles à la même droite (CD) ; leur intersection qui passe par M est
donc parallèle à (CD) : MN//CD. De même l’intersection de P et du plan de la face
CBD est aussi parallèle à ( CD) : SR//CD Donc , les droites ( MN) et ( SR) sont parallèles
.On démonterait d’une façon analogue que les droites ( MS) et ( NR) sont
parallèles. |
|
7°)Application pratique. Réalisation de surfaces
planes .
|
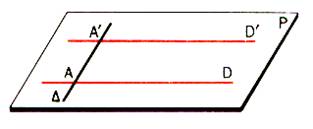
a) La droite D est appelée « génératrice » , se déplace
parallèlement à elle même à elle même en s’appuyant constamment sur la droite
Delta, appelée directrice . |
|
|
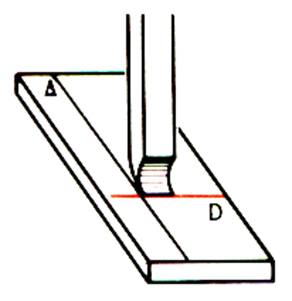
b) Certains procédés d’usinage du plan utilisent ce mode de génération à
l’aide de deux droites concourantes
dont une droite delta est fixe et
l’autre D se déplace parallèlement . (exemple : l’étau limeur ) |
|
CONTROLE:1°)Trouver des
exemples concrets de droites parallèles , de droite et plan parallèles , de
plans parallèles
EVALUATION: ( à voir)