|
DOSSIER : FONCTIONS LINEAIRES /
Mouvement uniforme / Objectif cours
50 |
|
|
||
|
Rappel : la définition de « mouvement » ou de
« non mouvement » implique
deux notions : le
temps (durée) et l’espace
parcouru. Si mouvement : nous faisons de la cinématique. ( le temps ‘s’
écoule ; la distance varie.) Si « non- mouvement » nous faisons de la
statique. ( le
temps ‘s’ écoule ; la distance ne varie pas.) |
||
|
A mettre en lien avec : La fonction linéaire |
||
|
A mettre en lien
avec : La fonction affine |
|
|
|
A mettre en lien
avec : Système sexagésimal et
système décimal |
||
|
A mettre en lien
avec : l ‘ Algèbre |
||
|
A mettre en lien
avec : Géométrie (équation du
premier degré) |
||
ENVIRONNEMENT du dossier:
|
Objectif précédent : 3°) cours spécifique sur @ la durée , @
travaux auto formatifs) |
Suivant : le
mouvement uniformément varié . |
|
|
|
|
|
|
DOSSIER : LE MOUVEMENT RECTILIGNE UNIFORME . |
|
|
|
|
|
|
|
Partie 1 : |
|
|
|
|
|
|
|
Partie 2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IV )
Représentation graphique des résultats précédents :: diagramme des vitesses , diagramme des
distances. |
|
|
|
|
|
|
|
·
Résumé. |
|
|
|
|
|
|
|
|
|
|
|
·
CALCULS TYPES : RESOLUTIONS de PROBLEMES par l’ ARITHMETIQUE |
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
Travaux pré requis: |
|
|
Travaux niveau VI et V |
||
|
|
|
|
Parcours : distance ;
vitesse : Dossier : fiche
« calcul d’une distance parcourue » 204 Dossier : « calcul de la vitesse »
.Fiche : 205 |
||||
|
|
|
||||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
On
désigne :
|
« mobile » |
tout
objet ou personne en mouvement dans un repère choisi. |
« Rectiligne »
|
|
|
COURS |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Notions : pour établir une « vitesse » il suffit de
mesurer la distance parcourue ( en mètre par
exemple) par un élève en un temps que l’on mesurera avec un chronomètre ( en
secondes) Ainsi
un élève qui parcours Si
l’on veut connaître la distance qu’il parcourrait en 1 heure ( = 3600 seconde), il suffit de multiplier « 5 par 3600 ». Ce
qui donne On
conclura qu’un individu qui court à la
vitesse de 5m/s ou de 18 k / h. Remarque :
le compteur d’une véhicule automobile (voiture ou d’une moto) donne une
vitesse que l’on peut appelée « vitesse instantanée » .Parce qu’elle
chaque à chaque instant. Pour
avoir une idée de la vitesse que l’on a mis pour se
déplacer d’un point à un autre il faut : relever sur le compteur
kilométrique la distance parcourue et calculer le temps mis pour effectuer
cette distance et effectuer le calcul. Pour
information : D’après les études statistiques : La vitesse moyenne
sur route, sur de longs trajets est de « rien ne sert de courir il faut partir à
point » « Vitesse » : la vitesse est
la distance parcourue en un temps
donné.
Il
faut toujours prêter attention aux unités indiquées :
Dans la
vie courante, on exprime souvent la
vitesse en kilomètres par heure.
Que l’on note : K / h ou
k .h-1 Mais on peut évaluer la vitesse en d’autres
unités :
on
dit : qu’un
avion à réaction parcourt qu’un
satellite se déplace à la vitesse
de qu’un
piéton parcours qu’un coureur à pied fait Que
la lumière se déplace à la vitesse de Que
le son
se déplace à la vitesse de |
|
|||||||||||
|
|
PARTIE 2 : Le« mouvement uniforme » |
|
|||||||||||
|
|
I ) Définition du mouvement rectiligne uniforme
. |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Exemple
2 :
(voir le dessin ci dessous) Un piéton marche sur en ligne
droite le long d’un canal. Il met constamment 90 secondes pour aller d’une
borne hectométrique ( de A à B , de B à C ; ……) à l’autre ( |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Un
mobile est animé d’un mouvement uniforme s’il parcourt des distances égales
dans des temps égaux , quels que soient les temps. Exemple
3 : Un mobile parcourt
La distance parcourue
pendant l’unité de temps est
constante : c’est ce que l’on appelle « la vitesse du mobile ». On écrira que
le mobile à une vitesse de Ainsi ; nous pouvons savoir quelle est la
distance parcourue par un mobile qui se déplace à la vitesse de 5 m/ s
en un temps donné : En 4 secondes , ce mobile
parcourt 5 En 8 secondes , ce
mobile parcourt 5 En
une minute et 15 secondes il a parcouru :
5 fois ( 60s + 15s
) soit 5
|
|
|||||||||||
|
|
On retiendra : qu ‘: Un mobile
est animé d’un mouvement rectiligne uniforme s’il parcourt sur une droite , toujours dans le même sens , des distances égales
en des temps égaux , si petits que soient ces temps. |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||
|
|
La
vitesse du mobile animé d’un mouvement rectiligne uniforme est constante. Reprise
de l’exemple 1 : En
90 s , le piéton parcourt En 1
seconde , il parcourt 100 : 90 =
1 , Sa
vitesse est donc de Si
nous prenons l’heure ( h ) comme unité
de temps , la vitesse est :
( que
l’on écrit aussi : soit 4000 m. h-1 ou Cette
vitesse est dite « constante » : V = constante est appelée « formule de la
vitesse) |
|
|||||||||||
|
|
On retiendra que : La vitesse d’un mobile animé d’un mouvement
rectiligne uniforme est mesurée par le même nombre que la distance parcourue pendant l’unité
de temps. |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
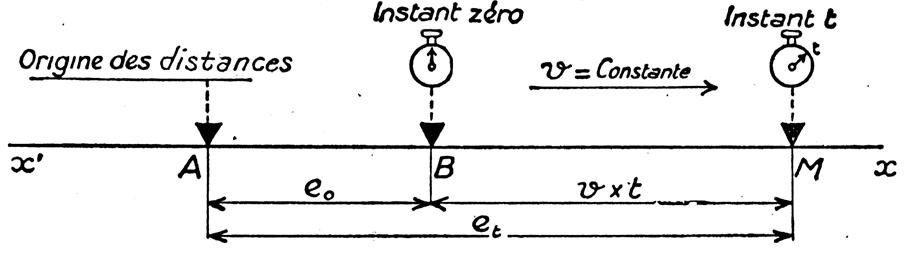
Distance à l’origine d’un mobile animé d’ un mouvement rectiligne uniforme. |
|
|||||||||||
|
|
Exemple : le piéton part d ‘un point « B » , à e0 = |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||
|
|
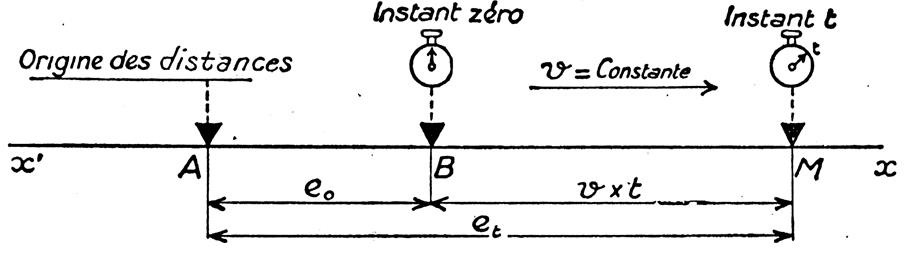
Ce
piéton se met en route et marche d’un mouvement uniforme à la vitesse v =
4 km .h-1 en s’éloignant
toujours de « A » . A quelle distance de
« A » est -il après t = 3 heures de marches ? En 1
h , le piéton parcourt une distance égale à : v
´ t = 4 ´ 1 = En 2
h , le piéton parcourt une distance égale à : v
´ t = 4 ´ 2 = En 3 h , le piéton
parcourt une distance égale à : v ´ t = 4 ´ 3 = Au bout de 3 h , le piéton est donc a une distance de « A » égale à : et =3
= 5
+ 12 = Remplaçons
les nombres par les lettres , nous obtenons l’égalité : |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Cette
égalité est appelée :
formule des distances |
|
|||||||||||
|
|
IV )
Lois des distances : |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||
|
|
|
|
Si l’on cherche à quelle distance
notée et (en
mètres) de l’origine des distances
« point O » se trouve au temps « t » (en seconde) un
mobile animé d’une vitesse « v » ( en mètres par
seconde).
On appliquera 2 lois
suivant le cas rencontré :
Première loi et
= v t si le mobile part de l’origine
« O »
Deuxième loi et
= eo + vt si le mobile a déjà parcourue une distance
|
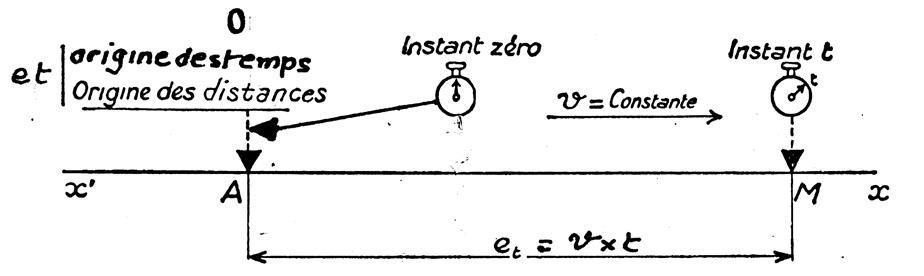
Si , à
l’instant initial, le mobile passe à l’origine des distances on a :
et = v t |
|
|
|
Si , à
l’instant initial, le mobile est déjà à une distance e o de l’origine des distances on a : et
= e o + v t Cette
formule, plus générale que la précédente, traduit la loi des distances (ou
des espaces ) |
|
|
IV ) Représentation graphique des
résultats précédents :
Remarque importante :
|
Dans la représentation graphique l’axe des « x » représente
le temps ; l’axe des « y » peut représenter l’espace
parcourue ou la vitesse.. |
|
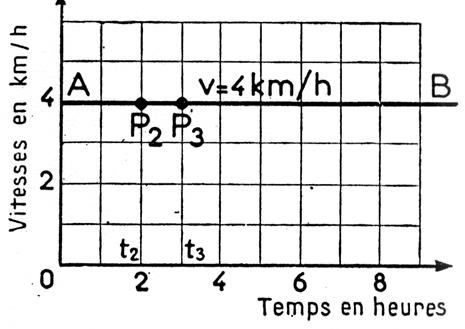
1°) Diagramme des
vitesses :
|
Lorsque nous avons tracé deux axes de coordonnées
rectangulaires , nous portons : En abscisses : les valeurs de temps
« t » (échelle : En ordonnées : les valeurs de la vitesse
« v » ( échelle : Plaçons le point « P2 » : A l ‘instant « t2 » = 2 h ,
la vitesse « v = 4 km/h » : Abscisse : O t2 = 5 ´ 2 = Ordonnée t2
P2 = 5 ´ 4 = Plaçons le point « P3 » : A l ‘instant « t 3 » = 3 h ,
la vitesse « v = 4 km/h » : Abscisse : O t3 = 5 ´ 3 = Ordonnée t3
P3 = 5 ´ 4 = Puisque la vitesse est constante , toutes les
ordonnées t2 P2
, t3 P3
etc. sont égales donc tous les points
« P2 » , « P3 »
sont sur une parallèle « AB » à l’axe des temps. |
La droite (AB) est le diagramme
de la vitesse du piéton ce diagramme représente le diagramme des vitesses
d’un mouvement uniforme. Dans un mouvement uniforme , le diagramme de la
vitesse est une droite parallèle à l’axe des temps. |
2°) Diagramme des distances
( à
l’origine d’un mouvement uniforme).
|
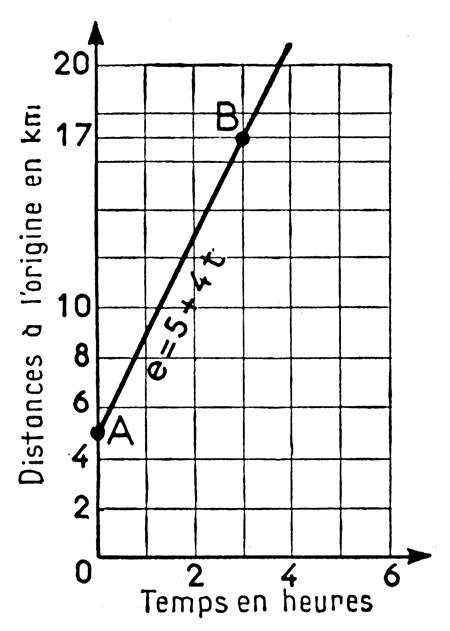
Cas 1 : à l’instant initial, le mobile est déjà à
une distance e o Nous portons : - En
abscisses : les valeurs du temps « t » ( échelle
choisie : - En
ordonnées , les valeurs de la distance
à l’origine « e » (
échelle : On choisit
2 points particuliers : Point « A » : Au temps t
= 0 ; e0 = Point « B » : Au temps t
= 3 ; e0
= soit 5
+ 4 fois 3
= 5 + 12 = Le diagramme des distances à l’origine est la
droite AB. |
|
|
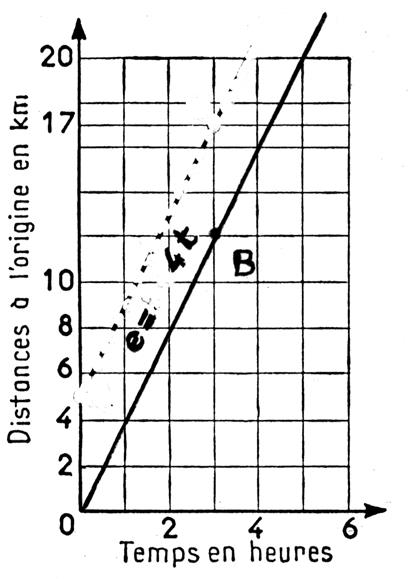
Cas 2 :à l’instant
initial, le mobile passe à l’origine des distance Nous portons : - En
abscisses : les valeurs du temps « t » ( échelle
choisie : - En
ordonnées , les valeurs de la distance
à l’origine « e » (
échelle : On choisit
2 points particuliers : Point « A » : Au temps t
= 0 ; e0 = Point « B » : Au temps t
= 3 ; e0
= soit 0
+ 4 fois 3
= 0 + 12 = Le diagramme des distances à l’origine est la
droite AB. |
|
Remarques :
Le diagramme
des vitesses uniformes en fonction du temps est une fonction de la
forme : y =
constante
Dans le 2ème Cas
: la distance parcourue associée à une
distance origine est une fonction
affine et se représente sur une
droite :
et=
eo +
vt ( forme y = ax +b )
Dans le 3ème Cas : La
distance parcourue est une fonction linéaire du temps et se représente graphiquement par une droite.
et
= vt ( forme y =
a x
)
|
1°) Un point est en
mouvement , par rapport à des points
fixes , pris comme repères , lorsque sa distance à l’un quelconque de ces points varie avec le
temps. 2°) La ligne suivie
par un point mobile dans son mouvement est la trajectoire de ce point. 3°) Pour étudier le
mouvement d’un point sur sa trajectoire , il faut choisir une origine des
distances et une origine des temps. 4°)Un mobile est
animé d’un mouvement rectiligne uniforme s’il parcourt une droite, toujours
dans le même sens , des distances égales en des temps égaux , si petits que
soient ces temps. 5°) La vitesse d’un
mobile animé d’un mouvement uniforme est « constante ». |
Etude du mouvement :
1°) Deux trains « A » et « B » ,
sont arrêtés sur des voies parallèles .
« A » démarre. Quelle est l’impression d’un voyageur de
« B » qui regarde fixement un wagon de « A » ?
Que faut -il pour s’assurer que son train ne
roule pas ?
« B » démarre
à son tour et accélère .Il rattrape « A » et roule à la même vitesse.
Quelle est l’impression du voyageur « B » qui regarde fixement
« A » ?
Enfin « B »
accélère et roule plus vite que
« A ». Quelle est l’impression du voyageur de « B » ?
CALCULS.
I - Une automobile roule sur une
ligne droite. L’indicateur de vitesse marque
1°) Calculer la vitesse en mètre par seconde.
2°) Calculer
la distance , en mètres, parcourue pendant ces 5 minutes.
3°) Tracer , pour cette période :
a)
le diagramme des vitesses.
b)
Le diagramme des distances à l’origine , sachant
qu’ à l’instant « zéro »
l’automobile est à
Pour les échelles
on prendra :
Pour les
temps :
Pour les
vitesses :
Pour les
distances à l’origine :
II ) Le mouvement d’une table de raboteuse est
conforme aux données suivantes :
-
longueur de course :
-
durée du trajet « aller » :30 s. (
mouvement uniforme)
-
durée du trajet retour : 15 s ( mouvement uniforme)
Tracer le diagramme des distances à l’origine d’un
point de la table (origine des distances : position du point à l’instant
où commence la course « aller ».)
Quelle est
la vitesse de coupe ?
Echelles : « Temps » :
III ) Un motocycliste part en voyage à 7 h 35 mn . Il consomme en moyenne
Au départ , le réservoir contenait
Etablir le
graphique du voyage avec les données suivantes :
IV ) Une voiture dont
le moteur tourne à 3 000 tr./mn
roule en prise directe. Les roues , compte tenue de l’écrasement des pneus , ont un diamètre de
1°) La vitesse horaire.
2°) Le régime du moteur
qui permettrait de conserver la même vitesse au véhicule monté sur roue de
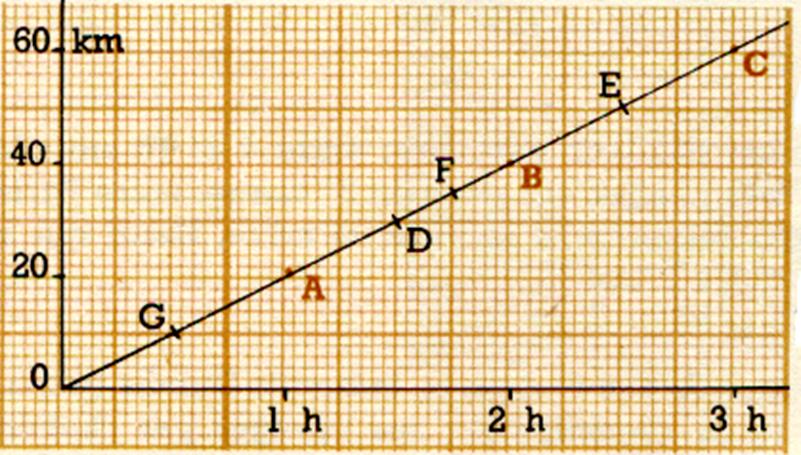
REPRESENTATIONS GRAPHIQUES : APPLICATIONS :
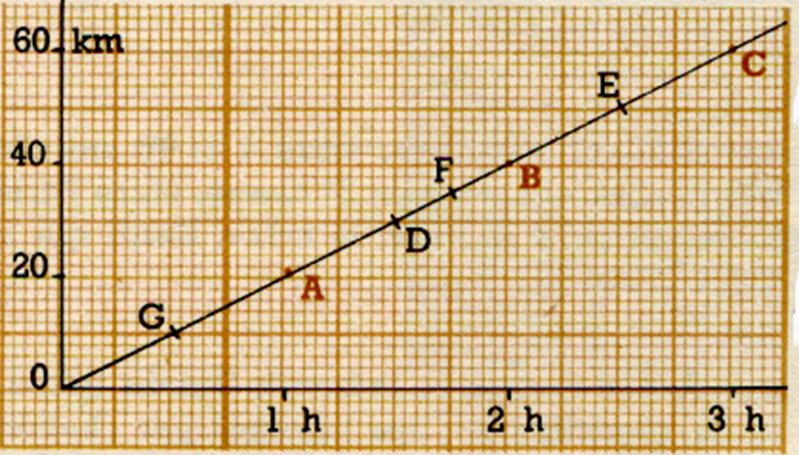
Nous représentons sur un papier quadrillé ,
millimétré de préférence, le mouvement d’un cycliste qui roule à 20 km/h :
|
|
|
En hauteur (ordonnée) , indiquons les
distances ; en largeur (abscisse) ,le
temps qui s’écoule ; chaque point A, B, C représente la position du
cycliste , par rapport au point de départ , au bout d’une heure , de 2 , de 3
heures …On pourrait aussi chercher des positions intermédiaires. Une ligne
qui joint les points A,B, C, représente toutes les positions du cycliste
pendant la durée de son déplacement : on y lit par exemple que le point
« D »représente la position après 1h 30 mn de route , à |
|
|
|
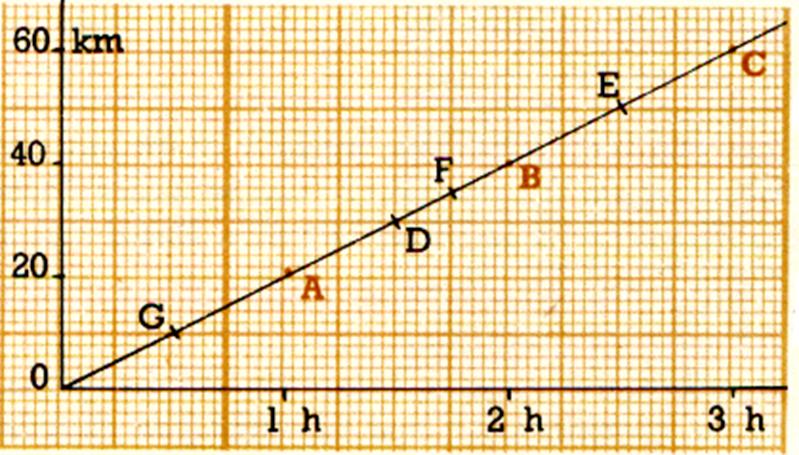
Sur le graphique ci-dessus : lire
à quelle durée , et distance
parcourue correspondent la position des points E, F ,G. Cherchez , sur la ligne des durées du graphique ,
les points qui correspondent à une durée de 1h15 mn ; 2h45 mn ;
0h15mn . En suivant les lignes du quadrillage , trouvez les points de la
ligne du mouvement qui leur
correspondent , et ,partant de ces points , trouvez les distances correspondantes auxquelles se trouve le
cycliste à ces moments-là. |
|
|
|
Le papier est millimétré ; quelle durée représente 1mm , sur le graphique ci dessus ? Quelle distance représente
1mm ?Sans calculs, par lecture du graphique , dites : a) à quelle distance du point de départ se trouvait le cycliste après 2 h
15 mn de route ; après 2h 39 mn au bout de combien de temps le cycliste se
trouvait à |
Etudes de
problèmes :
On distingue trois
éléments dans un problème d’étude du
mouvement uniforme :
1°) l’espace ou le
chemin parcouru par le mobile. ( e )
désignera l’espace parcouru . (exprimé
couramment en km ou en m )
2°) le temps ou la
durée du parcours. ( t )
3°) la vitesse ou
l’espace parcouru pendant l’unité de temps, c’est à dire pendant une seconde ,
une minute ou une heure. (v)
Si l’on connaît deux de ces valeurs on peut trouver la troisième .
Rappel sur le mouvement
uniforme :
|
e = v quand je connais la vitesse moyenne et la durée du parcours , je peux
calculer la distance parcourue. |
v est la vitesse "e" désigne
l' espace parcouru "t" temps (durée) |
|
On peut
donc en déduire :que v =
quand je connais la distance parcourue et la durée du parcours , je
peux calculer la vitesse moyenne, en divisant la distance parcourue par le
temps . |
La vitesse
d’un mobile est égale au rapport de la distance parcourue par le temps |
|
On peut
donc en déduire :que t =
quand je connais la distance parcourue et la vitesse moyenne , je peux
calculer la durée du parcours .en divisant la distance parcourue par la
vitesse. |
Le temps
mis pour parcourir une distance est égale à la distance parcourue divisée par
la vitesse . |
Comment faire :
Cela nous conduit à trois
principaux types de calculs :
|
Savoir
calculer une distance parcourue |
|
|
Savoir
calculer la vitesse |
|
|
Savoir
calculer la durée |
|
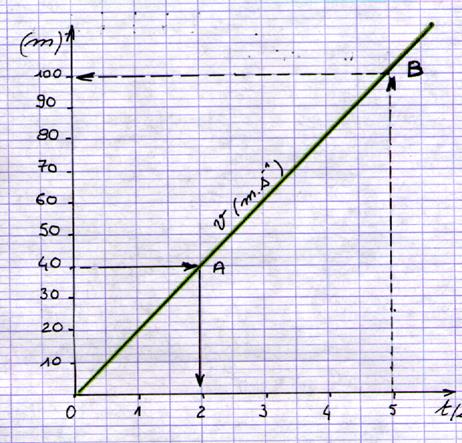
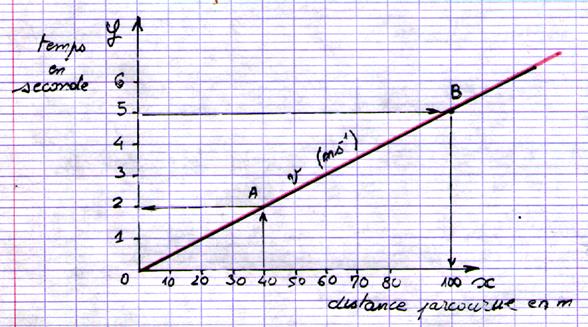
Représentation graphique de la vitesse moyenne :
|
La représentation graphique de la vitesse est une
droite . Etude du graphique : En A :
pour En B
en 5 sec. Il a été parcourue 100m . La vitesse est égale à la distance parcourue par
le temps : Pour La vitesse est égale à Soit v = 20 m/ sec ou 20m.sec.-1 |
|
|
Attention : la représentation
graphique ci contre n’est pas valable . Le temps doit être en
« x » ! |
|
CALCULS TYPES :
RESOLUTIONS de PROBLEMES. Par l’ ARITHMETIQUE :
1°) Calcul de
distance :
Quelle distance parcourt en 2 h 27 min un
cycliste qui roule à
|
Première solution : |
Deuxième solution |
|
réponse : durée du trajet en minutes : 2 h
27 min = 120 + 27 = 147 min en 60 minutes le cycliste parcours il parcourt x = x = |
Transformer 2 h 27 min (écriture sexagésimale en écriture décimale) : 1°) Transformation des « 27
min » en nombre décimal d’heure. 27 2°) 2 h 27 min =
2,45 h 3°) 30 fois 2, 45 = |
2°) Calcul de vitesse :
a )
Une automobile a parcouru
2h 15 mn = 135 mn
parcours moyen en 1
mn : 175,5 km : 135 (mn) =
vitesse par
minute :
vitesse par
heure : ![]() 60 (mn) =
60 (mn) =
b)
Quelle est la vitesse d’un train
qui effectue le parcours Chartres (borne :km 88 ) – Le Mans (borne : km 211)
en 1 h 7 min ?
(
|
Corrigé : |
|
|
Distance Chartres –Le Mans : 211 – 88 = Durée du trajet en minutes : 60 +7
= 67 min Le train parcourt En 1 minute il parcours : En 60 minutes il parcourt : Sa vitesse est de |
|
3°) calcul de temps :
a) un camion a parcouru
quelle a
été la durée du parcours ?
durée du parcours : 126 : 56 = 2h 15 mn (on divise la distance totale par la vitesse moyenne)
b) Combien de temps un piéton qui fait
|
Corrigé : |
|
|
Le piéton met 1 h pour faire 9 1h : 4 et pour faire 9 ,56 fois plus ,
soit :
|
9,56 : 4 = 2 ,39 h : soit 2 heures 2,39 –2 = 0,39 0,39 transformation en seconde : 23,40 – 23 = 0,40 0,40 conclusion : le piéton
mettra : 2 h 23 min 24 sec. |
PROBLEMES
FAISANT INTERVENIR PLUSIEURS MOBILES :
1°)
Cas de
MOBILES se déplaçant dans le même sens .
Une automobile quitte Paris à 10h 30min à la vitesse de
A quelle heure et à quelle distance de paris la deuxième
automobile rejoindra – t –elle la première ?
|
Corrigé : |
|
|
Avance de la première voiture : En une heure la 2ème voiture
parcourt : Durée de la poursuite en minutes :
Il sera alors : 10h 30min + 20 min
+ 1 h 40 min = 11h 90 min soit 12 h 30
min. Distance de Paris : elle
représente le trajet accompli par la 2ème voiture : |
|
D’une façon générale
lorsqu’un premier mobile est poursuivi par un second plus rapide , le temps mis
par ce dernier pour rejoindre le premier est le quotient de l’avance du premier
par la différence des vitesses .
Durée de la poursuite =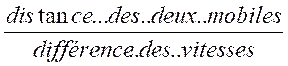
2°) Cas
de MOBILES se déplaçant en sens
contraire.
Deux
cyclistes partent à 13 heures de deux villes A et B distantes de
A quelle
heure se rencontreront – ils ?
Quelle sera
le distance la distance parcourue par chacun d’eux ?
|
Corrigé : |
|
|
En 1 heure la distance des deux cyclistes diminue de 30 +20 = Pour que cette distance diminue de Le premier à
parcouru : Le second a parcouru : |
|
D’une façon générale , lorsque deux mobiles vont l’un vers
l’autre , ils se rencontrent au bout d’un temps égal au quotient de leur
distance initiale par la somme de leurs vitesses.
Durée avant la
rencontre = 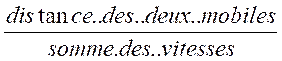
Résolution de problèmes par l’ algèbre
(système) :
Problème 1 :
Un voyageur
part à 8 h , sur une bicyclette à moteur , de la ville A pour la ville B ;
sa vitesse est de
1°) Solution algébrique :
Nous
prendrons pour unité de temps l’ heure et pour unité de longueur le kilomètre.
Soient
« x » le temps mis par le cycliste pour aller de A au point de
rencontre et « y » la distance de A au point de rencontre.
La distance
parcourue par le cycliste est y =
30x et la distance parcourue par l’auto
est : y = 50 ( x – 2 )
On a 30 x = 50
( x –2 )
20 x = 100
x = 5
on en
tire : y = 30![]() 5 = 150
5 = 150
Conclusion : l’auto rattrape donc le cycliste 5 h après le départ du cycliste ,
c’est à dire , à 13 h et à
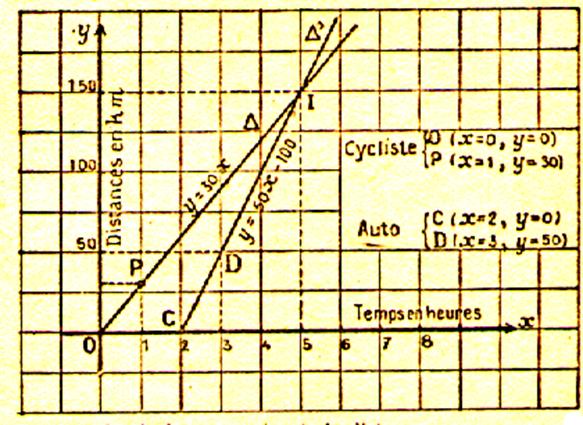
Solution graphique .
Prenons , comme
ci dessus , pour origine des temps , 8 h du matin ,
et pour origine des distances le point A.
Les
mouvements des deux mobiles se traduisent , d’après la formule des distances
par les équations :
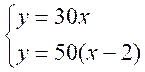 ou :
ou :
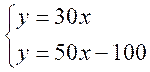
|
Représentation
graphique des deux fonctions : Les deux droites se coupent en un
point I dont l’abscisse
« x » = 5 indique le
temps au bout duquel a lieu la rencontre , 5 h après l’origine , soit 8 + 5 = 13 h l’ordonnée y = 150 du point I donne la distance (en km ) du point A au point de rencontre. |
|
Remarque .
la droite représentant le mouvement d’un mobile peut être construite sans qu’il soit nécessaire d’ écrire l’équation de cette droite. Ainsi
pour représenter graphiquement le mouvement du cycliste , on peut placer le point
O de coordonnées ( 0 ; 0 ) (au
temps 0 ,cycliste est au km 0) et le
point de coordonnées ( 1 ; 30 ) au
temps 1 , le cycliste est au km 30 ) il suffit de joindre OP.
Cette méthode est appliquée au problème suivant.
Problème 2 .
Deux villes
M et N sont distantes de
(Echelle
des temps :
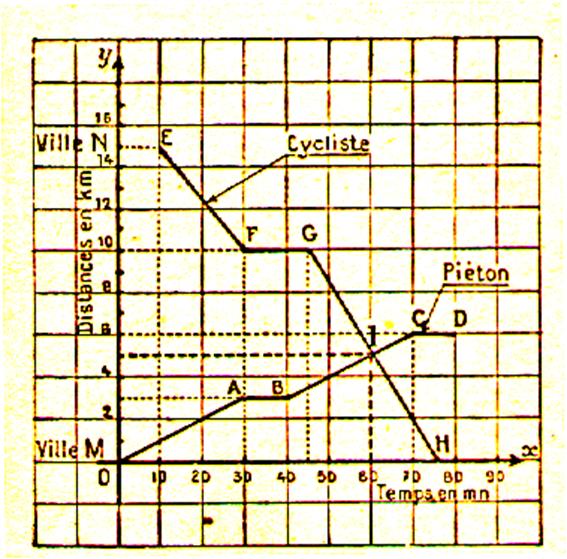
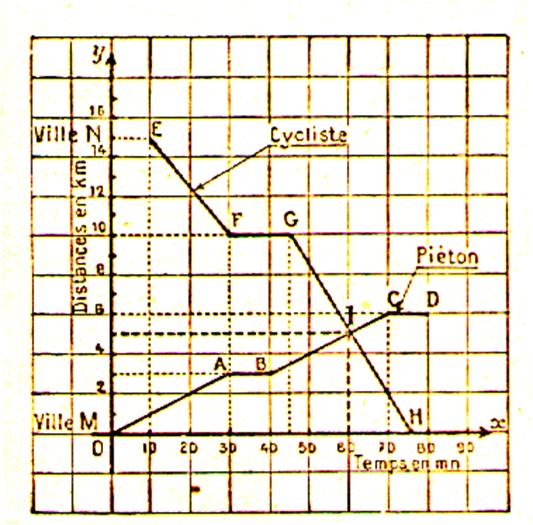
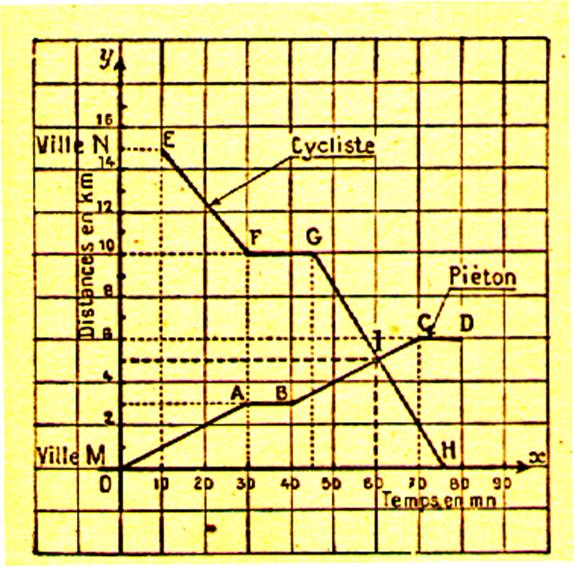
Solution graphique :
On prend
pour origine des temps 16 h (instant 0 ) et pour origine des
distances la ville M
|
1°) graphique du mouvement du piéton :à 16 h , le
piéton est en M (point 0 du graphique ,
x = 0 , y = 0 ) . A 16h 30 min le
piéton a parcouru les périodes de marche se traduisent
sur le graphique par des segments également inclinés sur Ox
et les arrêts par des segments parallèles à cet axe . |
|
|
2°) graphique du mouvement du
cycliste. A 16 h 10 min , le cycliste est en N (
point E du graphique , x = 10 , y =15
)A 16 h 30 min le cycliste n’est plus
qu’ à 15 - A 16 h 45 min , le cycliste , qui
s’est arrété pendant 15 min est toujours à Pour parcourir les 10 |
|
|
Analyse
des tracés : Le point d’intersection I des deux lignes permet de
lire : L’heure de la rencontre :
( x = 60 ) : 17 h La distance du point de rencontre à la
ville M : ( y = 5 ) : |
|
Dernier
exercice à savoir faire :
La
lumière, qui parcourt
TRAVAUX AUTO FORMATIFS .
1°) Qu’appelle-t-on « vitesse » ?
2°) Qu’appelle t-on
« mouvement uniforme » ?
4°) Donner la relation
mathématique liant entre : l’espace , le temps et la vitesse ; dans le
mouvement uniforme.
EVALUATION
Exercice I
|
|
|
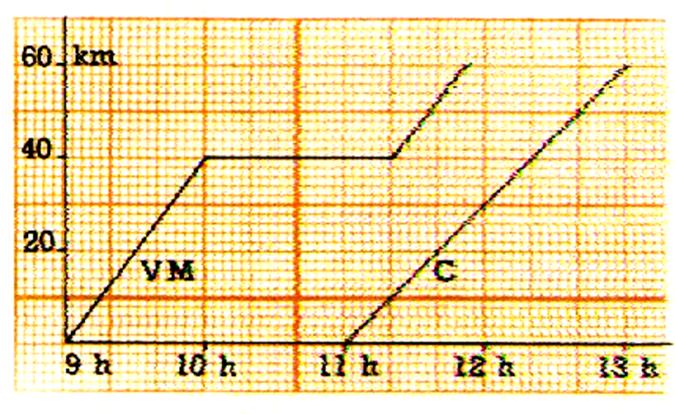
La ligne
« VM » du graphique ci-contre représente la marche d’un
vélomoteur , la ligne « C » celle d’un cycliste , qui ont a) A quelle heure part chacun d’eux ? b) Quelle distance parcourt le vélomoteur pendant la première
heure ? c) Il s’arête au 40e km. A quelle
heure repart-il ? A quelle heure arrive-t-il au bout du trajet ? A quelle vitesse roule cycliste ?A quelle
heure arrive-t-il au but de son voyage ? Combien de temps après le
vélomoteur ? |
|
Problème N°1 |
|
|
Un cycliste a
parcouru |
|
Problème
N°2
|
|
|
Un train omnibus a
fait |
|
Calcul de la
durée :
Problème
N°3
|
|
|
Une personne a un rendez vous à 9 heures à A quelle heure
doit-elle partir de son
domicile ? |
|
Problème
N°4
|
|
|
Un marcheur fait
du Quel temps met-il
pour parcourir 4 km ; 12
km ; 21 km ? Combien a-t-il parcouru dans la ville s’il s’est promené de 8 h
du matin à 19 h ,il s’est arrêté 1,5
heure pour se restaurer. |
|
Problème
N°5
|
|
|
La distance de
Paris à Boulogne est de A quelle heure
arrivera-t-il ? |
|
|
Problème N°6 |
|
|
Un employé demeure à |
|
|
Problème N°7 |
|
|
Combien de temps met
un automobiliste pour parcourir une distance de |
|
|
Problème N°8 |
|
|
Combien de temps met
un automobiliste pour parcourir une distance de |
|
|
Problème N°9 |
|
|
Combien de temps met
un automobiliste pour parcourir une distance de |
|
|
Problème N°10 |
|
|
Combien de temps met
un automobiliste pour parcourir une distance de |
|
|
Problème N°11 |
|
|
Combien de temps met
un cycliste pour parcourir une distance de |
|
|
Pour les
problèmes suivants il faut :
Savoir passer d’une écriture sexagésimale en écriture décimale |
Problème
N°12
|
|
|
Un camion parcourt |
|
Problème N°13
|
|
|
Un train circule à la
vitesse moyenne de Départ Paris , le
soir 21h38min Arrivée Bordeaux le lendemain matin à 6h50min Déterminer la distance
Paris Bordeaux par chemin de fer . |
|
PROBLEMES
N° 1 : Deux villes M et N sont distantes de
(Echelle
des temps :
N° 2 On prend pour origine des
temps 16 h (instant 0 ) et pour origine des distances la ville M
Un
voyageur part à 8 h , sur une bicyclette à moteur , de la ville A pour la ville
B ; sa vitesse est de
ARITHMETIQUE :
N°3) quelle
distance parcourt en 2 h 27 min un cycliste qui roule à
N°4
) Calcul de vitesse : Quelle est la vitesse d’un train qui effectue le parcours Chartres
(km 88 ) – Le Mans ( km 211) en 1 h 7 min ?
N° 5)
calcul de temps :
Combien de
temps un piéton qui fait
N° 6 ) Une automobile
quitte Paris à 10h 30min à la vitesse de
A quelle heure et à quelle distance de paris la deuxième
automobile rejoindra – t –elle la première ?
N° 7 ) Deux
cyclistes partent à 13 heures de deux villes A et B distantes de
A quelle
heure se rencontreront – ils ?
Quelle sera
le distance la distance parcourue par chacun d’eux ?
INTERDISCIPLINARITE
Vitesse d’un navire ou d’un avion :
Marins et aviateurs
utilisent des unités de vitesse particulières :
1°) le nœud est une
unité de vitesse qui équivaut à un mille
à l’heure.
Dire que la vitesse
d’un bateau est de 20 nœuds ou qu’il
« file 20 nœuds » revient à dire que sa vitesse est de 20 milles à l’heure soit :
l’ expression
« filer 20 nœuds » provient de l’ancien procédé utilisé pour mesurer
la vitesse d’un bateau . On lançait à la mer un flotteur (loch) relié au bateau
par une « ligne » de plusieurs centaines de mètre que l’opérateur
laissait « filer » entre les doigts. Cette ligne comportait un nœud
tous les
2°) le
mach est une unité de vitesse égale à la
vitesse du son dans l’air.
Cette unité , est utilisée uniquement par
les avions supersoniques dont la vitesse
atteint ou dépasse celle du son . Dans un air à 0° la vitesse du son est


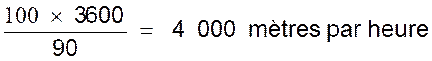
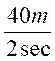 =
=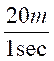
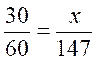
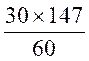
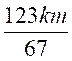
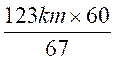
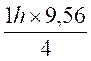
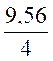
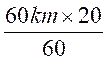
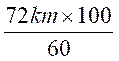
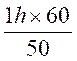
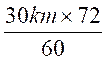
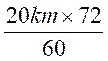
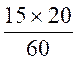 =
= 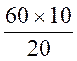 =30 min .Il arrivera en M à 16 h 45min + 30min = 17 h 15
min ( point H du graphique : x =
75 , y = 0)
=30 min .Il arrivera en M à 16 h 45min + 30min = 17 h 15
min ( point H du graphique : x =
75 , y = 0)