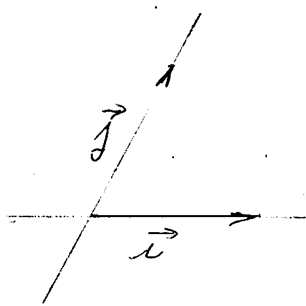Pré requis:
Détermination d’un point et les lieux géométriques
Quadrillage
Détermination d’un point
Graduation d'une axe
Droites sécantes
ENVIRONNEMENT du dossier:
INDEX « warmaths »	Objectif précédent : 1°) graduation et règle graduée ;… 2°) les graphiques	Objectif suivant : les repères ; exemples de repérages d’un point dans un plan .	Tableau 2°) Liste des cours sur le repérage

DOSSIER: LES REPERES CARTESIENS

	Cas Général .
	Cas particulier : les droites sont perpendiculaires, (on dit « orthogonale » )
	Caractéristiques : Les repères cartésiens peuvent être : normé s, non normés , orthonormés , non orthonormés .Le repère orthogonal.
	Première définition de "repère cartésien" .
	Deuxième définition : « repère cartésien »  et « base » .
	Norme des vecteurs unitaires .
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation

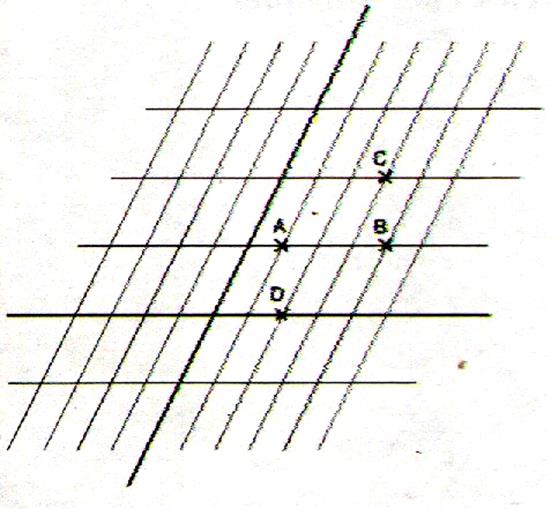
Cas Général : Le repère « cartésien » est constitué par l’intersection de deux droites orientées et graduées appelées « axe » (« axe » : voir repérage sur une droite) ; mettre en relation « droite orientée et nombres classés par ordre croissant de la gauche vers la droite » Le point d ‘intersection des deux « axes »est appelé «O »  (origine ,et départ des graduations)
Cas général :	Cas particulier : les droites sont perpendiculaires, (on dit « orthogonales » )
4 repères cartésiens se distinguent par la position des deux droites (perpendiculaires ou pas) et par la valeur des longueurs des graduations(identique ou différente) . « Position des droites » : le repère est dit : - « orthogonal »  (droites sécantes perpendiculairement , angle de 90°) - « non orthogonal » ( les droites sont sécantes « oblique » ,angle ¹ 90°) Ces droites sont ensuite « graduées » pour former des « axes gradués », «longueur des segments unitaires de graduation » : il est dit - « normé » : on dit « normé » si la longueur des deux segments unitaires est de la même mesure sur les deux droites sécantes, on qui que le repère est « normé» ; si d(O,I) = d (O,J) ; repère normé, (parfois on dit « ortho normal ») - « non  normé » : On dit « non normé » si la longueur des deux segments unitaires n ‘ a pas la même mesure sur les deux droites sécantes ,on qui que le repère est «non  normé» ; si d(O,I) ¹d (O,J) repère non normé.
Info  : « NORME d’un vecteur  ? »

Les différents repères	NORME	NON NORME
ORTHO (orthogonal)	repère Orthonormé L fig. 3)	repère ortho non normé L fig. 4)
NON ORTHO	repère non ortho normé L fig. 1)	repère non ortho non normé L fig. 2)

Première définition de "repère cartésien" :
On appelle « repère cartésien » : du plan , tout triplet : ( O, I , J ) Avec « O » est un point ; appelé « point d’origine » et : [ OI ] et [ O J ] sont les segments unitaires (norme), servant de « base » ,et de « référent pour graduer » les droites sécantes (axes) . Valeur des segments unitaires : « 1 ;  unité de mesure » (la valeur du segment unitaire est indépendante de sa longueur .(un segment unitaire vaut « 1 », il peut mesurer une longueur de 1,5 cm) Appartenance des segments unitaires : le segment [ OI ] appartenant à la droite « horizontale » ( droite des « x » ) le segment [ O J ] appartenant à la droite « oblique ou verticale  » ( droite des «y » ) voir : ligne horizontale, verticale, oblique.
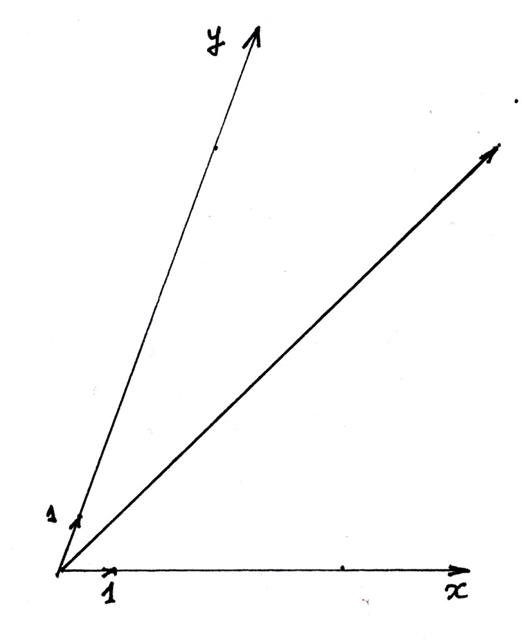
Deuxième définition : « repère cartésien »  et « base » :
(voir leçon : vecteurs et ses coordonnées)
On appelle « repère cartésien » du plan tout triplet ( O , , ) : Où: « O » est un point ( d ‘ intersection des droites sécantes ) et ( , ) est appelé « base » ,(formé par le vecteur «   » et le vecteur «   ») Précision : le point « I » étant l ‘ extrémité du vecteur «  » et le point « J » étant l ‘ extrémité du vecteur «   » Représentation graphique d'une base:
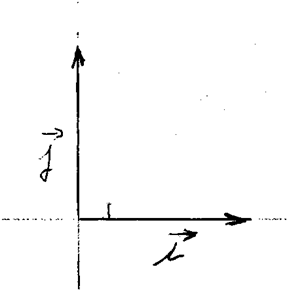
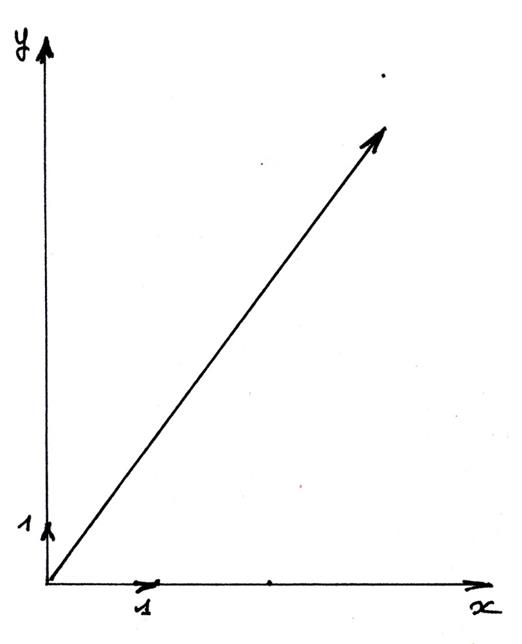
Représentation graphique d'une base:	d'une non base
Par définition : une base est un couple de vecteurs non colinéaires (donc non portés par des droites parallèles. Exemple : la base ( , )	Si les deux vecteurs sont portés par des droites parallèles ils ne peuvent pas former une base dans le repère cartésien.. Dans ce cas on dit que ces vecteurs sont colinéaires , ils ne peuvent former une base.
Les vecteurs formant une base servent à graduer les axes d'un repère
Représentation graphique d'une base:
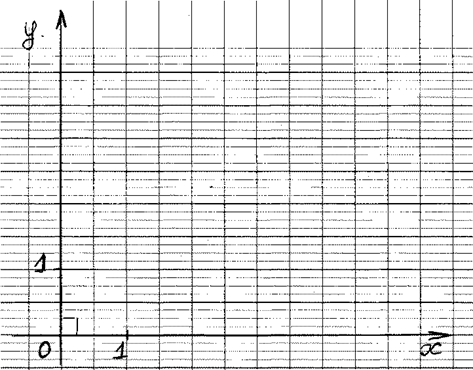
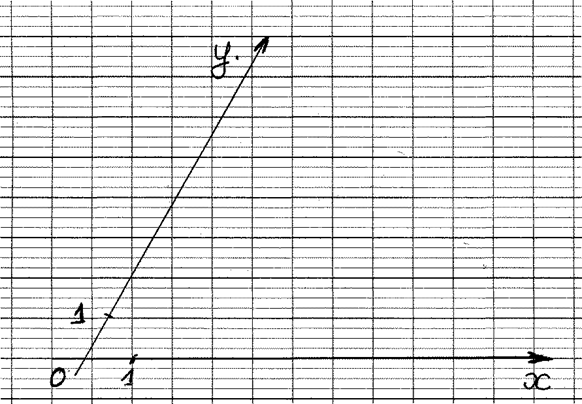
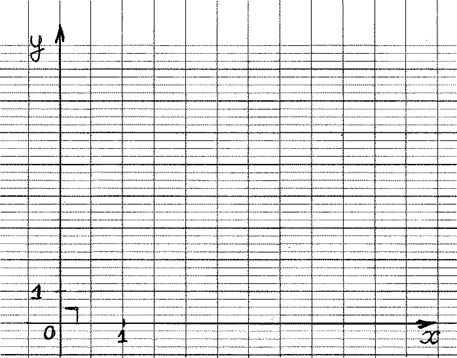
Dans un repère : ortho ; non- normé.	Dans un repère : non -ortho ; non- normé.
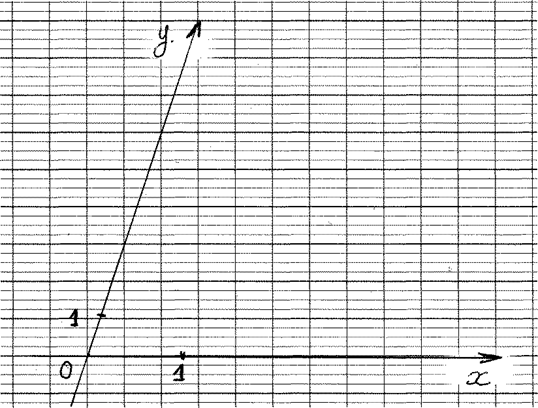
Dans un repère : ortho- normé.	Dans un repère : non – ortho ; normé.
Norme des vecteurs unitaires  : La norme des vecteurs unitaires vaut « 1 » ; ce qui se note : = 1 ; = 1
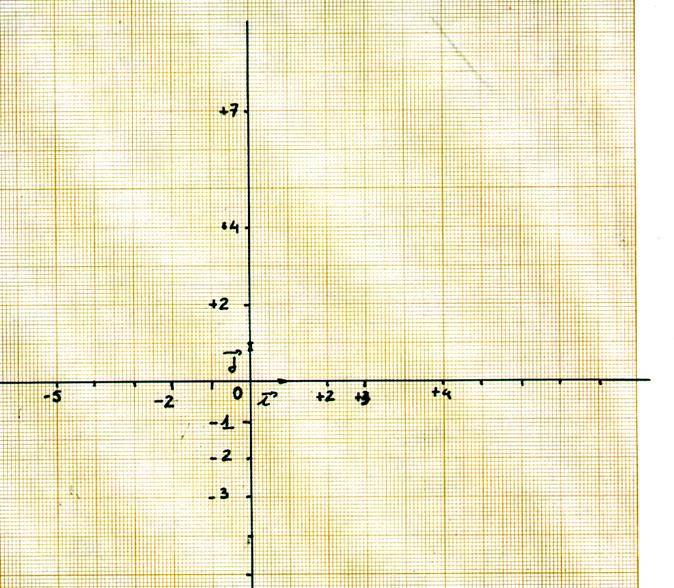
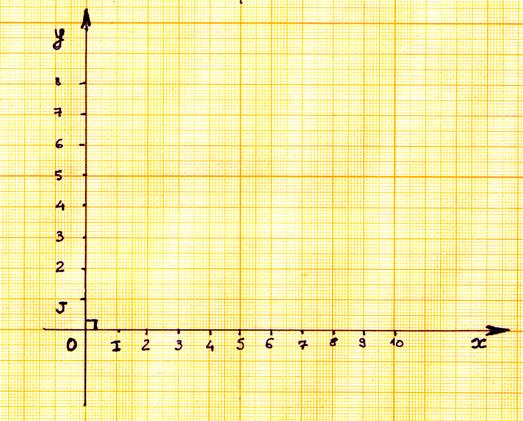
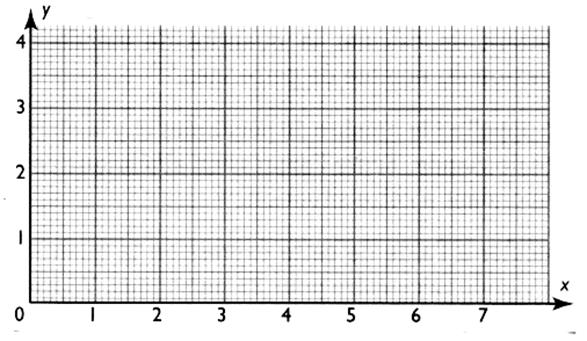
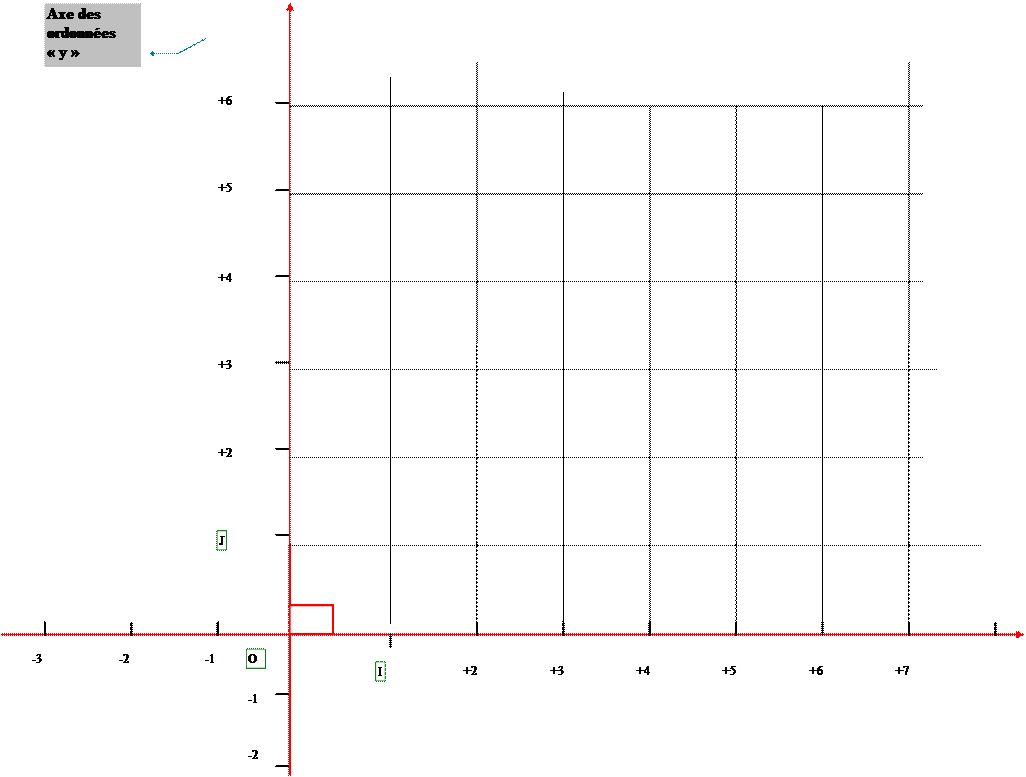
Exemple de construction d'un repère avec du papier millimétré L’axe horizontal s’appelle : Axe des abscisses : L’axe vertical s’appelle : Axe des ordonnées ( y , y’ )

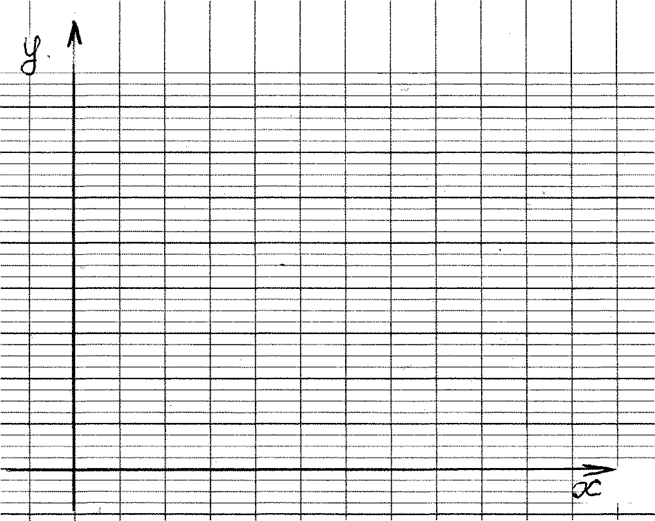
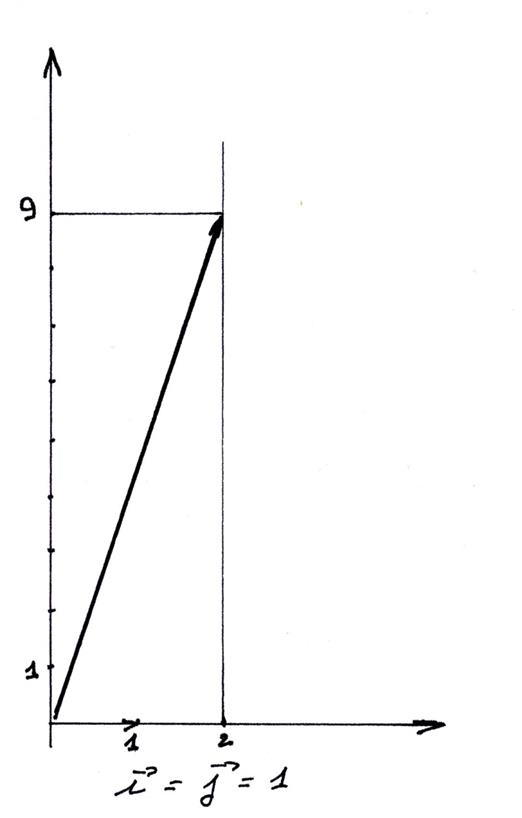
Représentation graphique du : repère cartésien « orthonormé » Ldit aussi « orthogonal »

D ( O ; I ) = d ( O ; J )
les 4 repères cartésiens sont : « orthogonal » ou « orthonormal »  et « non  orthonormal».
Caractéristiques : Les repères cartésiens peuvent être :
En résumé :
repère orthonormé : un repère orthonormé (orthonormal) est constitué de deux axes gradués perpendiculaires, la norme des vecteurs de la base , servant à graduer les axes ont la même norme sur les deux axes. On dit aussi :Les segments unitaires [OI] [OJ ]servant à graduer les deux axes ont la même longueur)
repère ortho non normé : ortho : un repère ortho non normé est constitué de deux axes gradués perpendiculaires , non normé : les graduations n ' ont pas la même norme sur les deux axes (les segments unitaires servant à graduer les deux axes n ' ont pas la même longueur)
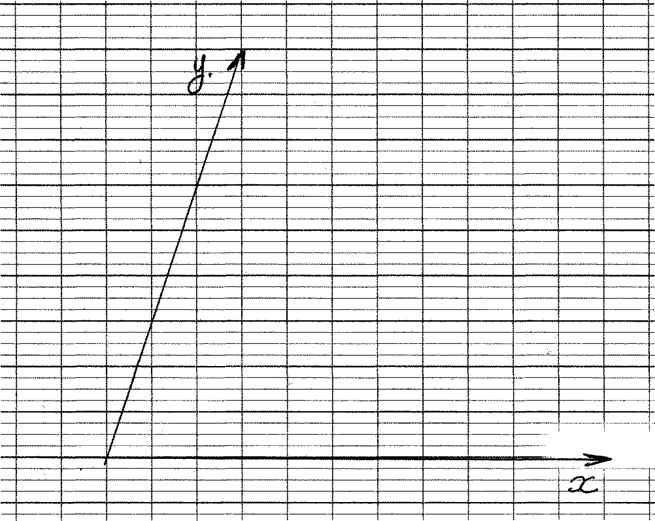
repère non ortho normé : L fig.2) non ortho : un repère non ortho normé est constitué de deux axes gradués non perpendiculaires normé : , les graduations ont la même norme sur les deux axes (les segments unitaires servant à graduer les deux axes ont la même longueur)
repère non ortho non normé : L fig. 1) Non ortho : un repère non ortho non normé est constitué de deux axes gradués non perpendiculaires , Non normé : les graduations n ' ont pas la même norme sur les deux axes (les segments unitaires servant à graduer les deux axes n ' ont pas la même longueur)
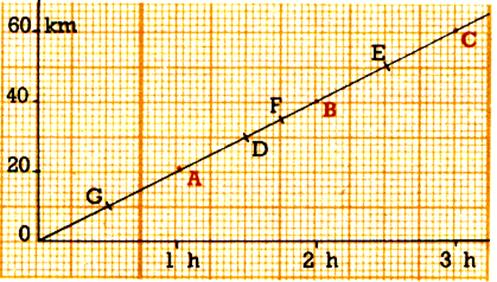
Application: les cartes géographiques
Exemples d'applications : - représentation d'un nombre de personnes en fonction de l'âge. - Les abaques. - Toutes les représentations graphiques des applications des fonctions linéaires
: Distance parcourue en fonction du temps.

Applications : pour le plaisir de faire des problèmes.

Application: pour le plaisir de faire des problèmes mathématiques.

Exemples de repères cartésiens couramment utilisés:

N°1

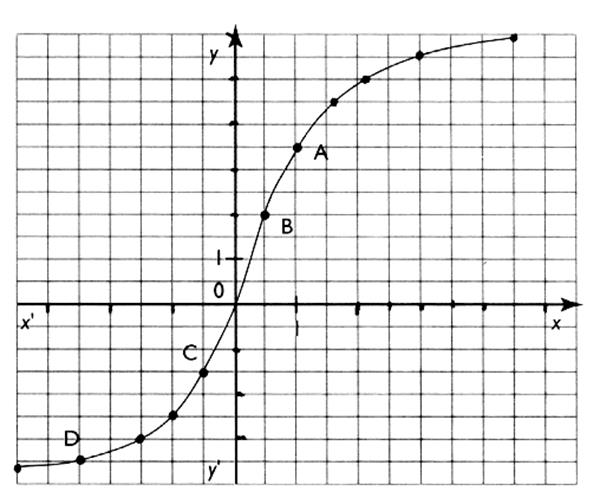
Exemple N°2 : dans ce repère est tracé une courbe .

TRAVAUX AUTO FORMATIFS.

CONTROLE :

Que signifie les mots :

« orthogonal » 

« non orthogonal »

« non  normé » :

« normé » :

Traduire en langage littéral :

( si d(O,I) = d (O,J) ; repère normé )

( si d(O,I) ¹d (O,J) repère non normé)

Donner une définition de « repère cartésien » :

Construire un repère cartésien orthonormé : d(O,I) = d (O,J)  = « 1, 5 cm )

dans un cadre de 15 cm par 15 cm

EVALUATION : DEVOIR : Compléter les repères suivants (mots et graduation):(terminer la graduation!)

Repérage d’un point dans un repère cartésien.
Evaluation (suite ) :
Série 1 :
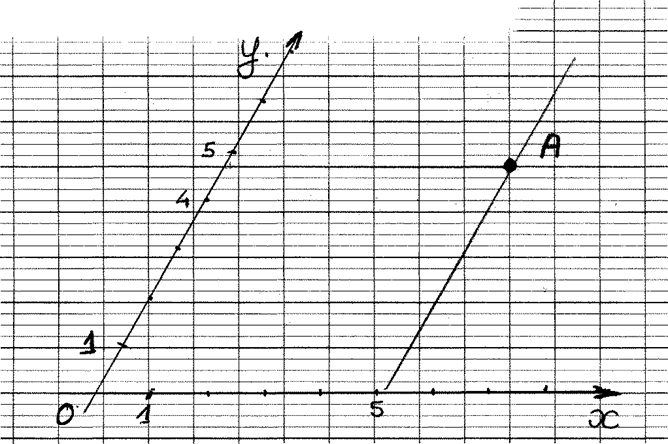
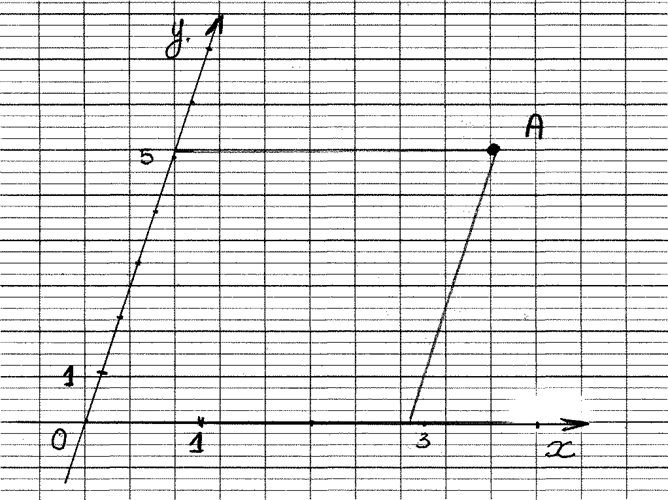
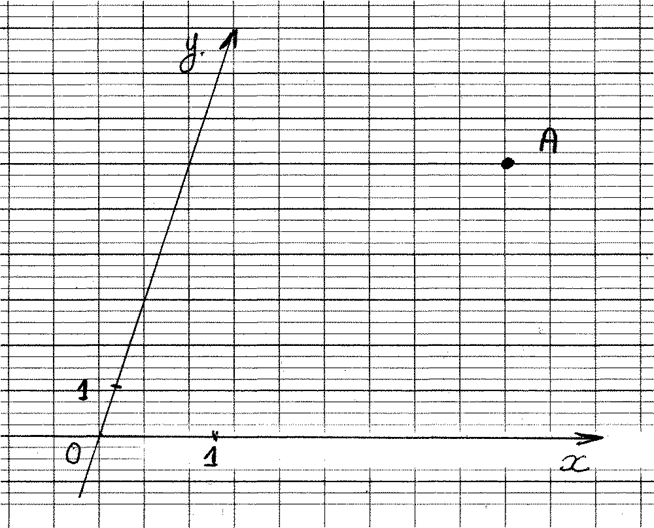
Donnez les coordonnées du point « A » .
A ( ….. ; ……)
.
A ( ….. ; ……)
A ( ….. ; ……)
A ( ….. ; ……)
Série 2 :
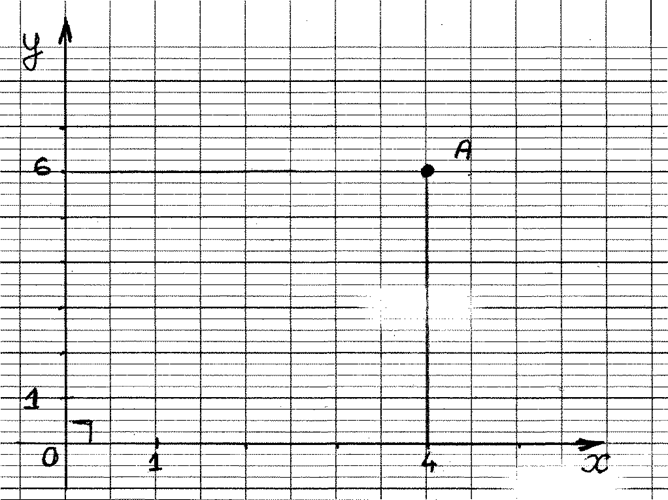
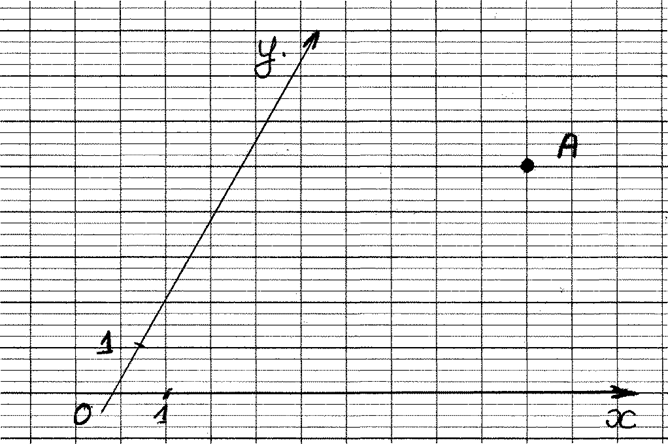
1°) Graduez les repères cartésiens . 2°) Donnez les coordonnées du point « A »
A ( ….. ; ……)
A ( ….. ; ……)
A ( ….. ; ……)