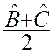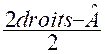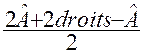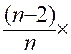Pré requis:

« lire un énoncé et Rédiger »
Collège : les définitions ;propriétés et description des quadrilatères
Collège : les définitions ; propriétés et description des triangles.
Liste des Objectifs

ENVIRONNEMENT du dossier:

Index warmaths

NOTIONS

Objectif suivant :

Suite

Liste des cours de géométrie plane

tableau

DOSSIER : « LA DEMONSTRATION » ou « résoudre un problème en géométrie. »

PARTIE 1 : La nécessité de bien connaître le cours :
- La figure ; L’hypothèse et la conclusion , la démonstration, 3 exemples ; …..
PARTIE 2 Présentation des principaux procédés de démonstration.
I) RELATIONS D’EGALITE Démontrer l’égalité de deux segments D et D’ a) D et D’ ne sont pas issus d’un même point . b) D et D’ sont issus d’un même point , II ) RELATIONS D’INEGALTES A) Inégalités entre segments de droite . B ) Démontrer que deux angles et ’ sont supplémentaires III ) RELATIONS DE POSITION OU DE FORME A) Démontrer que trois points A ;B ; C , sont alignés. B) Démontrer que deux droites D et D’ sont perpendiculaires. C ) Démontrer que deux droites D et D’ sont parallèles . D ) Démontrer que trois droites D ; D’ ; D’’ ; sont concourantes . E ) Démontrer que quatre points A ;B ;C ;D sont sur un même cercle . F ) Démontrer qu’une droite D est tangente à un cercle . G ) Démontrer que deux cercles sont tangents . H ) Triangles particuliers. :rectangle ; isocèle ; équilatéral I ) Le Parallélogramme . J) Parallélogrammes particuliers :rectangle ; losange ; carré K ) La droite des milieux dans le triangle ( fiches et activités) . IV) Calcul de la valeur d’un angle ,. A) l’angle « A » est un angle au centre , un angle inscrit , un angle intérieur ou extérieur par rapport à un cercle . B) L’angle A appartient à un triangle : C) L’angle A appartient à un quadrilatère convexe inscriptible. D ) L’angle « A » est l’angle intérieur d’un polygone régulier convexe de « n » côtés

COURS

Informations :

Les problèmes de géométrie ont pour objet soit la démonstration d’une proposition ou la découverte d’une propriété nouvelle , soit l’étude des déplacements simultanés des éléments d’une figure , soit la construction d’une figure conforme à des conditions données , soit l’évaluation de grandeurs géométriques : angles ; longueurs , aires ou volumes.

Il ne peut exister de règle générale permettant de résoudre automatiquement tout problème de géométrie .

Ce cours à pour vocation de donner des conseils qui suffiront pour trouver la solution dans la plupart des cas .

I ) NECESSITE DE CONNAITRE LE COURS :

La connaissance du cours est d’une absolue nécessité.

Il est impossible de chercher à résoudre un problème de géométrie si l’on ne connaît pas de mémoire les théorèmes sur lesquels se fonde la solution.

Il est impératif d’étudier attentivement les propriétés géométriques avant d’en faire l’application à la résolution des problèmes.

On peut affirmer que toute la difficulté provient souvent de l’ignorance du cours.

La FIGURE :

Tout problème de géométrie comporte une figure. Cette figure est la traduction graphique de l’énoncé ; elle doit être « exacte » et « complète » ; elle sera donc dessinée avec précision au moyen des instruments de dessin géométrique ( règle , décimètre , équerre , compas , rapporteur .Les égalités mentionnés dans l’énoncé seront indiqués ( par exemple : petits traits de même couleur pour des segments égaux ou pour des angles égaux , hachures pour les triangles, etc…)

Conseil : il faut réaliser une figure de dimensions moyennes ; trop réduite elle risquerait de n’être pas suffisamment claire ; trop grande elle ne permettrait pas de saisir aisément par une vue d’ensemble les liaisons de ses éléments.

Dans bien des cas une figure exacte guide utilement les recherches .

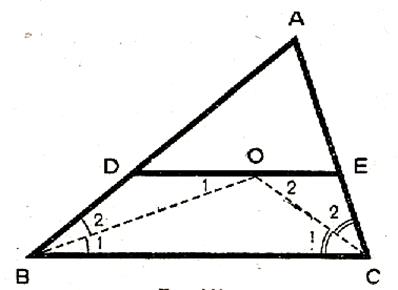
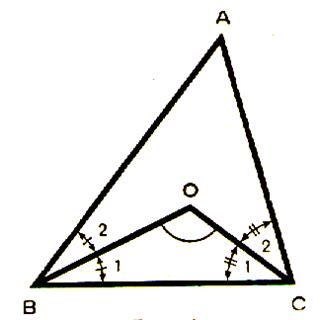
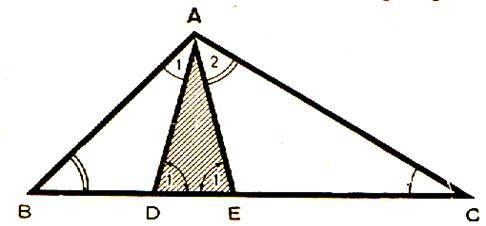
L’hypothèse et la conclusion :

Une lecture attentive de l’énoncé permet de dégager l’hypothèse , c’est à dire l’ensemble des données supposées connues , de la conclusion , proposition qu’il s’agit d’établir .

La démonstration :

La démonstration consiste à établir entre l’hypothèse et la conclusion un enchaînement logique des propositions. Ces propositions sont des « définitions » et des « théorèmes » de cours qui , par associations d’idées , se présentent à l’esprit lorsque l’on examine attentivement les conditions de l’hypothèse , et qu’on analyse minutieusement la figure afin de saisir les relations mutuelles de ses éléments.

Dans la plupart des problèmes , la solution ne peut être obtenue directement par application d’un seul théorème ; on procède par étapes successives , chaque nouveau résultat mettant en lumière de nouvelles propriétés . On choisit parmi elles celles qui permettent de faire un nouveau pas vers la conclusion ; on passe ainsi par degrés du connu à l’inconnu jusqu’à ce que l’on parvienne à la solution.

Exemple 1 :

Démontrer que la parallèle à un côté d’un triangle menée par le point de concours de bissectrices est égale à la somme des segment adjacents à ce côté qu’elle détermine sur les deux autres.

Hypothèse :

(1) DE parallèle à BC

(2) L’angle B₁=l’angle B₂

(3) L’angle C₁=l’angle C₂

Conclusion : DE = BD + CE

La donnée (1) suggère le théorème :si deux droites parallèles sont coupées par une sécante , les angles alternes internes , ou correspondants ,sont égaux entre eux .

Après examen de la figure, ce théorème est appliqué aux parallèles DE et BC coupées par les sécantes BO et CO.

Ainsi

l’angle B₁=l’angle O₁ ; l’angle C₁=l’angle O₂

Combinant ces résultats avec les données (2) et (3) on obtient :

l’angle O₁ = l’angle B₂ ; l’angle O₂ = l’angle C₁

Ces égalités d’angles dans les triangles BDO et CEO entraînent l’application du théorème : si deux angles d’un triangle sont égaux , ce triangle est isocèle .

D’où BD = DO , CE = OE , et en définitive DE = BD +CE

Remarque :il est facilement visible sur une figure que les triangles BDO et CEO sont isocèles et que , par conséquent , BD = DO , CE = CO

D’où BD + CE = DO +OE

La marche à suivre découle donc de la figure : démontrer que les triangles BDO et CEO sont isocèles.

Exemple II :

Démontrer que , dans un triangle ABC , l’ angle O formé par les bissectrices des angles B et C vaut 1 droit +

Hypothèse :

(1) L’angle B₁=l’angle B₂ =

(2) L’angle C₁=l’angle C₂ =

Conclusion :

= 1dr +

On nous demande d’établir une relation entre les angles O et A des triangles BOC et BAC ; nous appliquons donc successivement à ces deux triangles le seul théorème permettant de calculer la valeur d’un angle intérieur d’un triangle en fonction des deux autres : la somme des angles intérieurs d’un triangle vaut deux droits .

Nous obtenons :

= 2dr - ( ) ; =2 droits – (+)

soit en tenant compte des données (1) et (2)

= 2 droits -

=2 droits – (+)

Les seconds membres de ces égalités établissent une relation évidente entre et

= +

voulant obtenir une relation exclusivement entre et nous calculons

en fonction de ( application du théorème ci dessus)

d’où = + = =1dr +

Tracé de lignes auxiliaires :

Dans certains cas , la figure telle qu’elle résulte de l’énoncé ne suffit pas ; elle doit être compléter par le tracé de lignes auxiliaires , prolongements , parallèles , perpendiculaires , symétriques , etc…,dont le rôle est de faire apparaître de nouvelles figures ou d’établir des relations entre des éléments apparemment distincts.

Autre méthode : A la méthode de raisonnement qui consiste à partir de l’hypothèse pour aboutir à la conclusion on peut , dans certains cas , préférer la méthode inverse , c’est à dire remonter à l’hypothèse en étudiant les conséquences de la conclusion . C’est ainsi , qu’on résout généralement les problèmes de construction. De l’étude des propriétés de la figure réalisée empiriquement on déduit la construction de cette figure .

En se qui concerne plus particulièrement les démonstrations , on peut combiner les deux méthodes et après avoir établi l’enchaînement des propriétés des géométriques dans le sens conclusion hypothèse conclusion pour obtenir la solution définitive.

Exemple III :

Dans un triangle ABC on mène jusqu’au côté BC une droite AD faisant avec le côté AB un angle égal à l’angle C et une droite AE faisant avec le côté AC un angle égal à l’angle B .

Démontrer que le triangle ADE est isocèle .

Hypothèse :

₁ = et ₂ =

Conclusion : tr DAE isocèle

Si le triangle DAE est isocèle les angles à la base ₁ et ₁ sont égaux ; or ces angles sont extérieurs respectivement aux triangles ABD et ACE.

Un angle extérieur est égal à la somme des angles intérieurs non adjacents :

₁=₁ + ; ₁= ₂ +

d’où ₁ + = ₂ + , relation qui découle immédiatement de l’hypothèse.

Raisonnement par l’absurde.

Ce mode de raisonnement est souvent employé pour la démonstration des réciproques consiste à établir le bien fondé d’une conclusion en montrant que toute autre conclusion serait contraire à l’ hypothèse ou à un théorème précédent , généralement le théorème direct.

MISE AU NET DE LA SOLUTION

La solution ayant été trouvée , on dresse le plan au brouillon afin de faire apparaître l’enchaînement logique des arguments ;

Exemple 1

DE parallèle . BC :

₁=₁

₂=₁

Déductions

₁=₂

₂=₂

tr DOB et EOC isocèles

Conclusion :

Hypothèse :

Puis on l’établit au net , ce qui se ramène à un travail de composition française .Les qualités d’une telle rédaction sont la rigueur et la précision. Pour chaque argument on indiquera la partie de la figure à laquelle il se rapporte , la proposition ( hypothèse , construction, définition ou théorème) qui le justifie , la conclusion qu’il permet d’énoncer. Le style sera clair , la phrase simple , aussi courte que possible .

Les explications seront suffisantes pour être comprises ; cependant on devra éviter le « délayage »qui affaiblit toujours le raisonnement. On réservera les abréviations pour le brouillon ; il serait inconvenant de les faire figurer dans la solution définitive . Les énoncés des théorèmes rappelés seront soulignés (il sera d’ailleurs inutile de répéter plusieurs fois un même théorème au cours d’une solution ).

Suite à cette étude sommaire des principales méthodes de démonstration , nous indiquerons les procédés le plus couramment utilisés pour résoudre un certain nombre de problèmes élémentaires , tels que : établir l’égalité de deux segments ou de deux angles , prouver que deux droites sont perpendiculaires ou parallèles , que deux angles sont supplémentaires ….,etc…

PARTIE 2 Présentation des Principaux procédés de démonstration.

I) RELATIONS D’EGALITE

Démontrer l’égalité de deux segments D et D’

a) D et D’ ne sont pas issus d’un même point .

b) D et D’ sont issus d’un même point ,

II ) RELATIONS D’INEGALTES

B) Inégalités entre segments de droite .

B ) Démontrer que deux angles et ’ sont supplémentaires

III ) RELATIONS DE POSITION OU DE FORME

C) Démontrer que trois points A ;B ; C , sont alignés.

D) Démontrer que deux droites D et D’ sont perpendiculaires.

C ) Démontrer que deux droites D et D’ sont parallèles .

D ) Démontrer que trois droites D ; D’ ; D’’ ; sont concourantes .

E ) Démontrer que quatre points A ;B ;C ;D sont sur un même cercle .

F ) Démontrer qu’une droite D est tangente à un cercle .

G ) Démontrer que deux cercles sont tangents .

H ) Triangles particuliers. :rectangle ; isocèle ; équilatéral

I )le Parallélogramme .

J) Parallélogrammes particuliers :rectangle ; losange ; carré

IV) Calcul de la valeur d’un angle

A) l’angle « A » est un angle au centre , un angle inscrit , un angle intérieur ou extérieur par rapport à un cercle .

B) L’angle A appartient à un triangle :

C) L’angle A appartient à un quadrilatère convexe inscriptible.

D ) L’angle « A » est l’angle intérieur d’un polygone régulier convexe de « n » côtés

I) RELATIONS D’EGALITE

Démontrer l’égalité de deux segments D et D’

a) D et D’ ne sont pas issus d’un même point .

1) On peut faire entrer D et D’ dans des triangles dont on établit l’égalité ( les éléments homologues de deux triangles égaux sont égaux )

On peut montrer que :

2) D et D’ sont deux côtés opposés d’un parallélogramme ;

3) D et D’ sont deux cordes qui appartiennent à un même cercle (ou à des cercles égaux) et sous- tendent

Des arcs égaux ou sont équidistants du centre .

Théorèmes appliqués :

Deux triangles sont égaux lorsqu’ils ont :

a) Un côté égal adjacent à deux angles égaux chacun à chacun .

b) un angle égal compris entre deux côtés égaux chacun à chacun.

c) Les trois côtés égaux chacun à chacun.

Deux triangles rectangles sont égaux lorsqu’ils ont :

a) l’hypoténuse et un angle aigu égal.

b) L’hypoténuse égale et un côté de l’angle droit égal .

Dans un parallélogramme les côtés opposés sont égaux.

Dans un même cercle ou dans des cercles égaux :

1°) à des arcs égaux correspondent des cordes égales ;

2°) des cordes équidistantes du centre sont égales .

C ) D et D’ sont issus d’un même point .

Mais ils ne sont pas dans le prolongement l’un de l’autre.

1) D et D’ sont les côtés latéraux d’un triangle isocèle

Dans un triangle isocèle , aux angles égaux sont opposés des côtés égaux .

2) D et D’ sont deux obliques qui s’écartent également du pied de la perpendiculaire .

Deux obliques issues d’un même point et qui s’écartent également du pied de la perpendiculaire sont égales .

3°) D et D’ sont deux tangentes à un même cercle issus d’un point commun

Deux tangentes à un même cercle issues d’un même point sont égales.

REMARQUE : dans certains cas l’égalité de D et D’ s’établira en calculant la longueur de chacun d’eux ou en démontrant que D et D’ sont égaux à un même troisième segment ou encore que D et D’ sont la somme ou la différence de segments égaux .

II ) RELATIONS D’INEGALTES

A) Inégalités entre segments de droite .

Voici les théorèmes les plus usités pour établir une inégalité entre les segments de droite .

1°) Le segment de ligne de droite est la plus courte distance d’un point à un autre	INFO 1 ? ? ?
2°) Si , d’un point , l’on mène à une même droite la perpendiculaire et une oblique , la perpendiculaire est plus courte que l’oblique .	Info 2 ? ? ? Et INFO 2bis
3°)Si deux obliques issues d’un même point s’écartent inégalement du pied de la perpendiculaire , celle qui s’en écarte le plus est plus grande .	Info 3 ? ? ?
4°) Dans un triangle , au plus grand angle est opposé le plus grand côté , et réciproquement .	Info 4 ? ? ?
5°) Dans un triangle , un côté quelconque est inférieur à la somme des deux autres et supérieur à leur différence .	Info5 ? ? ?
6°)Dans un cercle ou dans deux cercles égaux , des cordes , inégalement distantes du centre sont inégales ,et la plus rapprochée est la plus grande .	Info 6 ? ? ?

B ) Démontrer que deux angles et ’ sont supplémentaires .

On peut montrer que :

1°) et ’ sont des angles internes

(ou externes )d’un même côté d’une sécante coupée par deux parallèles .

Si deux parallèles sont coupées par une sécante , les angles internes (ou externes )d’un même côté de la sécante sont supplémentaires .

2°) et ’ ont leurs côtés parallèles ou perpendiculaires et ne sont pas égaux .

Deux angles dont les côtés sont parallèles ou perpendiculaires sont égaux ou supplémentaires ;

3°) et ’ sont des angles opposés d’un quadrilatère convexe inscrit .

Les angles opposés d’un quadrilatère convexe inscrit sont supplémentaires.

III ) RELATIONS DE POSITION OU DE FORME

A) Démontrer que trois points A ;B ; C , sont alignés.

On peut établir que :

1°) est un angle plat	Info ? ? ?
2°) AB et BC forment des angles opposés par le sommet , égaux , avec une droite passant par B	Info ? ? ?
3°) AB et BC sont parallèles à une même droite .	Info ? ? ?

B) Démontrer que deux droites D et D’ sont perpendiculaires.

On peut montrer que :

1°) D et D’ sont les côtés de l’angle droit d’un triangle rectangle
2°) D est la base d’un triangle isocèle , D’ est la médiane ou la bissectrice issue du sommet principal.	Dans un triangle isocèle , la médiane issue du sommet principal est hauteur et bissectrice de l’angle au sommet .
3°) D et D’ sont bissectrices de deux angles adjacents supplémentaires .	Les bissectrices de deux angles adjacents supplémentaires sont perpendiculaires.
4°) D et D’ sont les diagonales d’un losange .	Les diagonales d’un losange sont perpendiculaires .
5°) D est tangente à un cercle et D’ porte le rayon qui aboutit au point de contact.	Le rayon qui aboutit au point de contact est perpendiculaire à la tangente .

Cas particulier : Pour démontrer qu’une droite est médiatrice d’un segment AB , on peut démontrer que deux points de cette droite sont équidistants de A et de B.

C ) Démontrer que deux droites D et D’ sont parallèles .

On peut montrer que :

1°) D et D’ sont perpendiculaires à une même droite.	Deux droites perpendiculaires à une même troisième sont parallèles entre elles ;
2°) D et D’ sont coupées par une sécante et forment des angles alternes internes , correspondants égaux ; des angles internes ou externes d’un même côté de la sécante supplémentaires.	Si deux droites coupées par une sécante forment des angles alternes internes , correspondants égaux , des angles internes ou externes d’un même côté de la sécante supplémentaires , ces deux droites sont parallèles .
3°) D et D’ sont deux côtés opposés d’un parallélogramme .	Par définition , les côtés opposés d’un parallélogramme sont deux à deux parallèles .
4°) D et D’ sont deux cordes interceptant entre elles des arcs égaux ;	Théorèmes sur les arcs interceptés par deux cordes parallèles .
5°) D et D’ sont parallèles à une même droite	Conséquence du postulat d’ Euclide
6°) la droite des milieux dans un triangle est parallèle à la base ; dans un trapèze elle est parallèle aux bases.

D ) Démontrer que trois droites D ; D’ ; D’’ ; sont concourantes .

a) D ; D’ ; D’’ ; sont les médiatrices , les hauteurs , les bissectrices ou les médianes d’un triangle .

b) On établit que le point d’intersection de D et D’ a des propriétés telles qu’il appartient à D’’ .

Remarque : Dans certains cas la connaissance des propriétés suivantes peut être utile :

1)les diagonales d’un parallélogramme inscrit dans un autre parallélogramme passe par le centre de celui-ci .
2°)Les bissectrices intérieures des angles inscrits dans un même arc de cercle passent par le milieu de l’arc intercepté.
3°) Toute droite équidistante des extrémités d’un segment est parallèle à celui-ci ou passe par son milieu.

E ) Démontrer que quatre points A ;B ;C ;D sont sur un même cercle .

On peut monter que :

1) les quatre points sont équidistants d’un point fixe.

2) Le quadrilatère ABCD est inscriptible , c’est à –dire que :

a) ou bien deux angles opposés sont supplémentaires

c) ou bien d’un côté , AB par exemple , est vu sous le même angle des deux sommets C et D .

En particulier deux triangles rectangles ayant l’hypoténuse commune et situés soit de part et d’autre , soit d’un même côté de cette hypoténuse forment un quadrilatère inscriptible dans un cercle ayant comme diamètre l’hypoténuse commune .

F ) Démontrer qu’une droite D est tangente à un cercle .

On peut montrer que la distance du centre à la droite est égale au rayon , autrement dit , la droite est perpendiculaire à l’extrémité du rayon.

Remarque : Pour démontrer qu’un cercle est tangent à une droite « D » en un point « A » , il faut démontrer que :

1°) le point A est sur le cercle .

2°) Le rayon OA est perpendiculaire à la droite D .

G ) Démontrer que deux cercles sont tangents .

On peut montrer que la distance des centres est égale à la somme ou à la différence des rayons . Dans le premier cas , les cercles sont tangents extérieurement ; dans le second cas , ils sont tangents intérieurement .

H ) Triangles particuliers.

Pour démontrer qu’un triangle est …..On peut établir qu’il satisfait à l’une des conditions suivantes :

Rectangle

a)il a un angle droit ( ou deux de ses angles sont complémentaires)

b)la médiane relative à l’un des côtés est égale à la moitié de ce côté (qui est l’hypoténuse ).

c)il est inscriptible dans un demi cercle .

Isocèle

a) il a deux côtés égaux ;

b) il a deux angles égaux ;

c) l’une des hauteurs est aussi médiane (ou bissectrice)

d) il a un axe de symétrie ;

Equilatéral

a) il a ses trois côtés égaux ;

b) il a ses trois angles égaux ;

c) il est isocèle , et a un angle de 60° ;

d) il a trois axes de symétries .

I ) Parallélogramme .

Pour démontrer qu’un quadrilatère convexe est un parallélogramme , on peut établir qu’il satisfait à l’une des conditions suivantes :

1) les côtés opposés sont deux à deux parallèles .
2°) les côtés opposés sont deux à deux égaux .
3°) Deux côtés opposés sont à la fois parallèles et égaux .
4°)les angles opposés sont deux à deux égaux.
5°) les diagonales se coupent en leur milieu .

J ) Parallélogrammes particuliers

Pour démontrer qu’un parallélogramme est :	On peut établir qu’il satisfait à l’une des conditions suivantes :
Un rectangle	a)il a un angle droit et b)ses diagonales sont égales
Un losange	a) ses côtés consécutifs sont égaux ,et b) ses diagonales sont perpendiculaires c) ses diagonales sont bissectrices des angles .
Un carré	C’est à la fois un rectangle et un losange.

IV) Calcul de la valeur d’un angle

A) l’angle « A » est un angle au centre , un angle inscrit , un angle intérieur ou extérieur par rapport à un cercle .

Appliquer le théorème correspondant sur la mesure d’un angle :

1°) L’angle au centre a même mesure que l’arc qu’il intercepte .
2°) L’angle inscrit a même mesure que la moitié de l’arc qu’il intercepte.
3°)L’angle intérieur a même mesure que la demi- somme des arcs interceptés par ses côtés et leurs prolongements.
4°)l’angle extérieur a même mesure que la demi- différence des arcs qu’il intercepte .

B) L’angle A appartient à un triangle :

1°) est l’un des angles intérieurs du triangle et la somme des deux autre angles et est connue : =2 droits – (+)
2°) est un angle extérieur du triangle , et la somme des angles intérieurs non adjacents et est connue : _ext =+

C ) L’angle A appartient à un quadrilatère convexe inscriptible.

L’angle opposé est connu :

=2 droits –

D ) L’angle « A » est l’angle intérieur d’un polygone régulier convexe de « n » côtés

=180°

Remarques : dans certains cas :

a) est la somme ou la différence d’angles calculables séparément .

b) Le complément ou le supplément de sont connus .

CONTROLE:

A voir

EVALUATION: