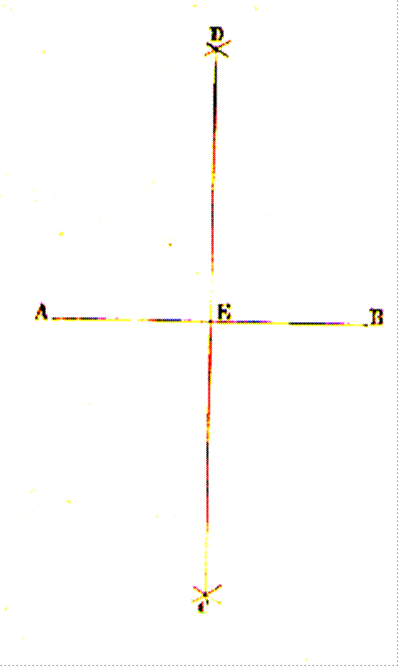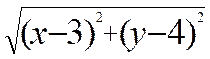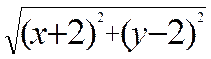Niveau 5    CAP industriel.

Géométrie :  DOSSIER : TRACES GEOMETRIQUES/  /  Objectif cours 17

 

Pré requis:

 

Lecture :   …
L' angle droit
Perpendiculaires : tracés
Les droites perpendiculaires

 

ENVIRONNEMENT du dossier:

 

Index warmaths	Objectif précédent :  1°) Les droites 2°) Les droites remarquables dans un triangle. 3°)  Complément : fiche activités découvertes « médiatrice » de travaux collège ( 6ème )	Objectif suivant 1°)propriétés  2°) les axes de symétries 3°) recherche du centre d’un disque ou cercle	Info. Géné. tableau    Liste des cours disponibles en  géométrie plane

DOSSIER :   La MEDIATRICE (définition et tracé )  d’un segment.

 

1°)Définition :

2°) Médiatrice et tracé

3°) Médiatrice et axe de symétrie 

4°) médiatrice et distance.

5°) médiatrice  et équation.

4°)Médiatrices et recherche d’un centre d’un cercle.

5°) Médiatrices et centre du cercle circonscrit à un triangle.

 

 

 

TEST	COURS	Devoir  Contrôle	Devoir évaluation	Interdisciplinarité		Corrigé Contrôle	Corrigé évaluation
		Complément : fiche de travaux collège ( 6ème )		>>>Fiches travaux

 

 

 

 

 

 

 

COURS

 

On doit toujours associer à « médiatrice » le mot « segment ».

On trace ou on « construit » la médiatrice d’un segment .

 

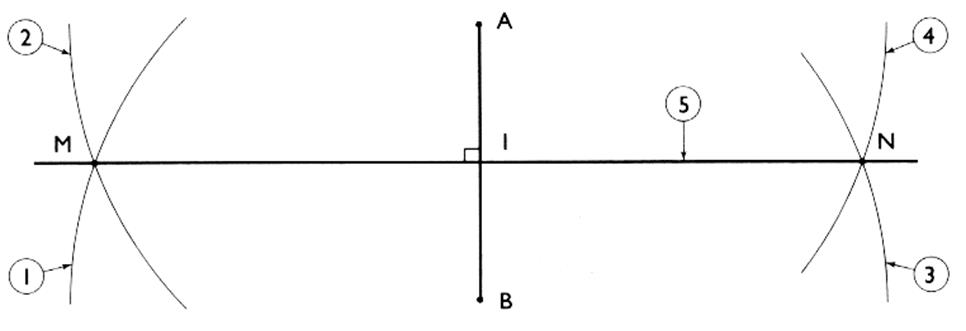
ou  lorsque l'on a pas  de place d'un côté de la ligne :

1°) Définition :

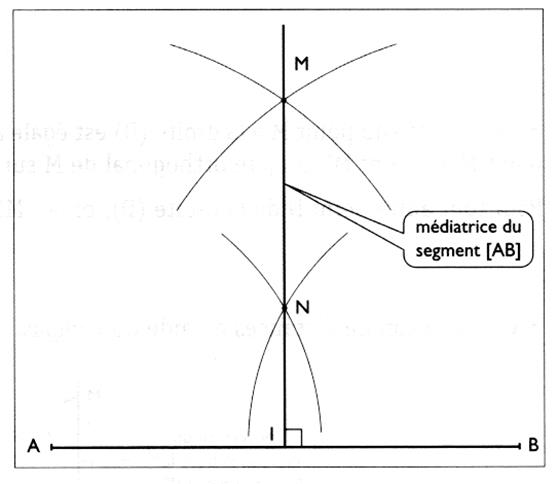
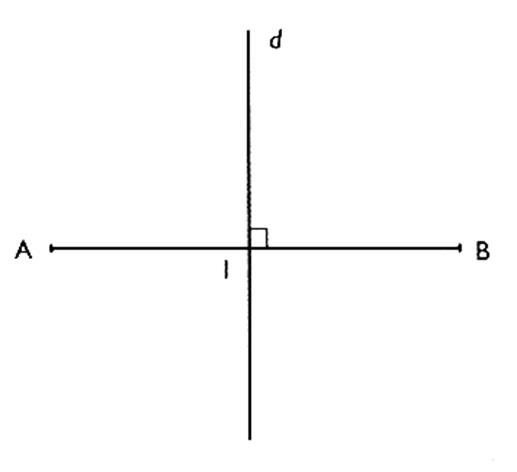
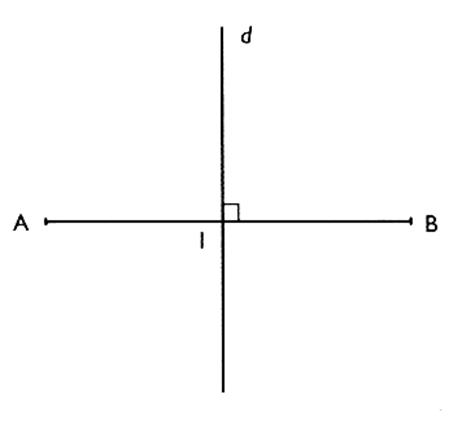
Si l'on trace un segment de droite AB  ,si l'on plie de manière à amener A sur B  ,on obtient une droite "d" (par pliage)  perpendiculaire  au  milieu  du segment. On peut donc  énoncer : qu'une médiatrice est une droite perpendiculaire au milieu de ce segment .

 2°) CONSTRUCTION D'UNE MEDIATRICE :

A ) TRACER d’une médiatrice  d’un segment  en utilisant  le compas et la règle.

Construction de la médiatrice d'un segment
Soit une droite AB donnée ; des points A et B ; comme centre de cercle  ,avec une ouverture de compas plus grande que la moitié de AB ,on décrit deux arcs de cercle qui se coupent en C et D ; on joint ces deux points par une droite ; cette droite est perpendiculaire à la ligne AB , et , de plus elle la partage en deux parties égales au point E.

: On en déduit qu'une médiatrice est aussi un axe de symétrie

 

 

B ) TRACER une médiatrice L avec la règle graduée et l’équerre .

Dans l’ordre  : il faut  mesurer la longueur du segment ;diviser cette longueur par deux ; à partir d’ une extrémité  ( A ou B ) placer le  point  "I"   milieu du segment ; placer l’équerre  sur le segment , mettre le bord perpendiculaire de l’équerre au point « I » ; tracer un trait perpendiculaire partant de ce point "I"  , avec une règle prolonger ce trait de chaque coté du segment .(ce trait  perpendiculaire est la médiatrice du segment) .

 

3°)Médiatrice et distance :  ( 4^ème )

 

Ensemble des points équidistants de deux points donnés :

L’ensemble des points équidistants de deux points donnés est une droite passant par le milieu du segment borné par ces deux points  . On l’appelle médiatrice du segment .

 

Exemple : L’ensemble des points équidistants de deux points donnés A et B est une droite passant par le milieu de [AB]  . On l’appelle médiatrice du segment AB.   d (A,I)  =   d ( I, B) d (A, M)  =   d ( M, B) d ( N , A)  =   d (N, B) d (A,P)  =   d ( P, B) vérification : deux façons : - il suffit de mesurer par exemple : d (A,I)  et   d ( I, B) avec une règle ; Prendre un compas  et une ouverture de d (A,I)  et comparer  avec d ( I, B)

 

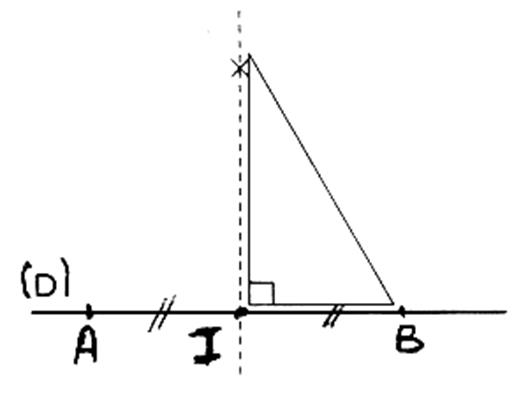
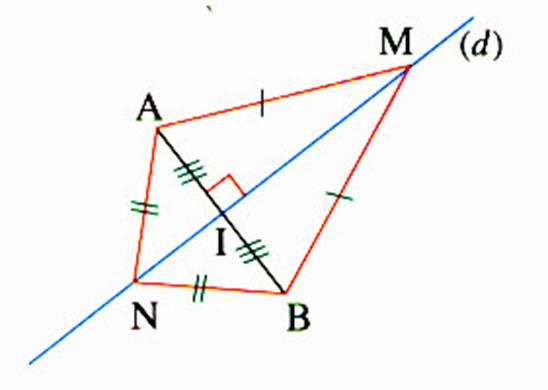
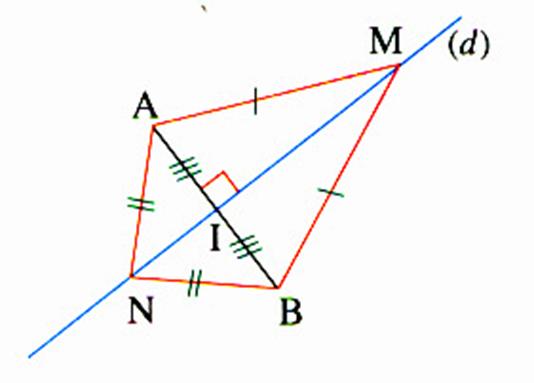
Si l'on place un point M sur la médiatrice ,si l'on mesure la distance entre les deux extrémités ,on constate que ce point est à égale distance de A et B .Plaçons un point N , nous constatons que celui ci se trouve également  à égale distance des extrémités.

Hypothèse : la droite (d) est la médiatrice d’un segment AB
Conclusion : MA = MB , NA = NB ; I est milieu de [AB]  et l’angle   est droit

Ainsi :  la médiatrice d’un segment  [AB]  est l’ensemble des points équidistants de A et B.

Une médiatrice   est un alignement de points situés à égal distance  des extrémités d'un segment de  droite .

 

Plus particulièrement :

1°)  la médiatrice d’un segment  [AB]  est l’ensemble des points équidistants de A et B. ( équidistants  signifie : situés à la même distance ; à égale distance)   2°)  la médiatrice est la perpendiculaire à la droite AB  « notée : ( AB) »   qui passe par le milieu  I du segment AB . « noté :  [AB] »

 

 

4°)  Médiatrice est  un axe de symétrie

Cet alignement de points est une droite  passant par les segment [MN]  ; cette droite est  appelé  "axe de symétrie" des extrémités du segment [A B].

 

 

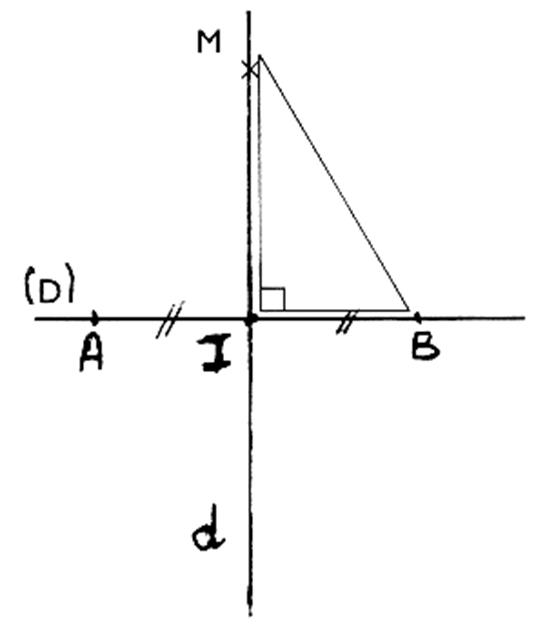
Tracé d'une médiatrice :

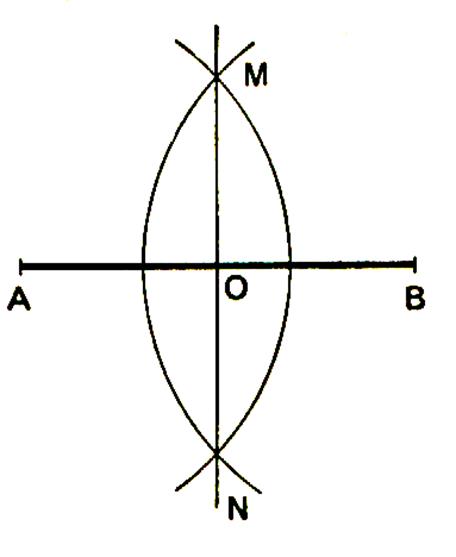
On trace la droite (AB) support du segment AB ; elle partage le plan en deux demi – plans P1 et P2. Les points A et B étant indiqués : -   La pointe du compas en A :  Avec un compas tracer deux arcs de cercle de centre A et de rayon  R >  d ( A, B)   ; l’un dans le  demi plan P1 et l’autre dans le demi plan P2   . -    La pointe du compas en B :      Avec un compas, tracer deux arcs de cercle de centre B et de même rayon  que précédemment :R > d ( A,B )   ; l’un dans le  demi plan P1 et l’autre dans le demi plan P2   . Constat : les points d’intersection des arcs M et N obtenus , détermine les points de passage de la droite  appelée «  médiatrice du segment AB » ; cette droite médiatrice passe par le milieu de son segment.

 

 

5°) MEDIATRICE et EQUATION :  « situation problème » destinée au niveau classe 3^ème

 

Exemple : soit deux points  A ( 3 ;4) et B (-2 ;2) ; et un point  M ( x ; y ) trouver l’équation de la médiatrice de A et B  passant par M.

M ( x, y) appartient à la médiatrice si et seulement si : d ( M,A) = d (M,B) , d’ où :     =  en élevant « au carré »les deux membres  de cette égalité  et en développant nous obtenons : x2 – 6x + 9 + y2  - 8y + 16 = x2 + 4 x+ 4 + y2  - 4y + 4   ce qui donne après simplification ; l’équation cherchée : -10 x – 4 y +17  = 0 soit  4 y =  - 10 x +17   ; l’équation de la droite médiatrice du segment AB est :                          y =  - 2,5 x + 4,25

Tracer un repère orthonormé , - Placer les deux points « A » et « B ». - Tracer avec une équerre la médiatrice du segment ; -  placer sur la droite « médiatrice » dessus un point « M ».

 

 

INFO 1 :  Voir   MEDIATRICE et recherche du centre d’un disque.
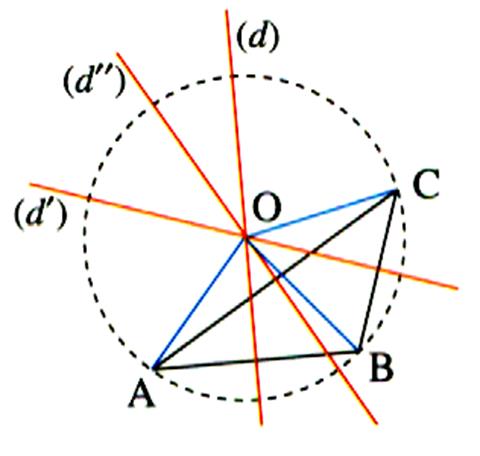
Soit deux cordes quelconques AB et une autre CD ; on trace la médiatrice de ces deux segments . Le point d’intersection des deux médiatrices et le centre du disque.

 

INFO 2 : les médiatrices du triangle et le centre du cercle circonscrit.
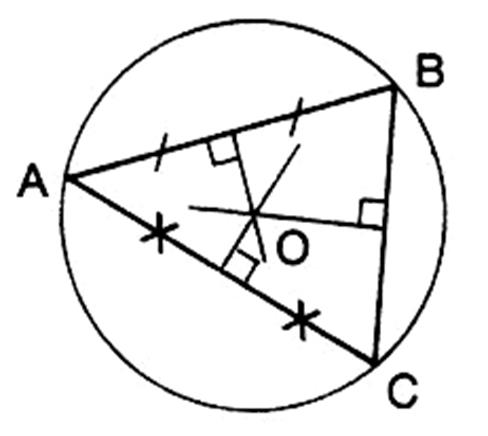
a) Centre à l’intérieur du disque	b) centre à l’extérieur du disque

 

 

 

 

Compléments d’informations :

	Voir activités 5ème collège fiche 8
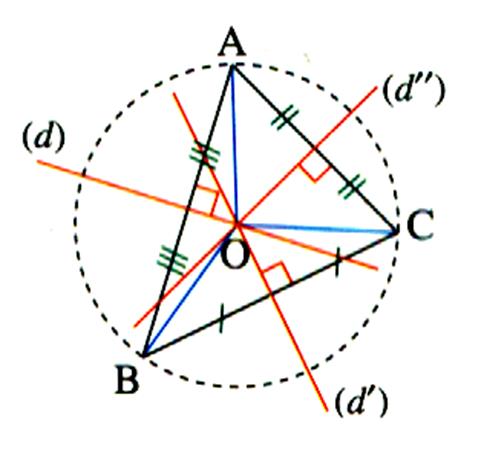
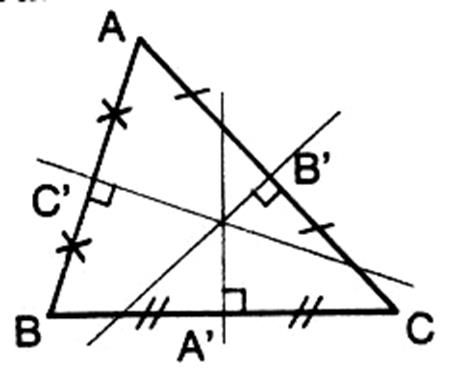
Dans un triangle les médiatrices se coupent en un même point.	Avec un compas ;on peut tracer un cercle qui passe par les trois points de ce triangle.

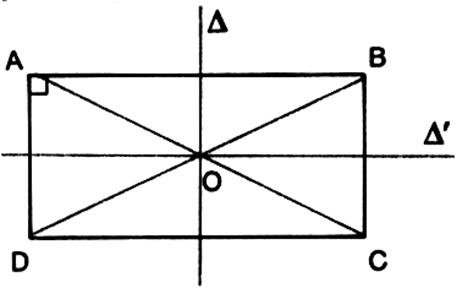
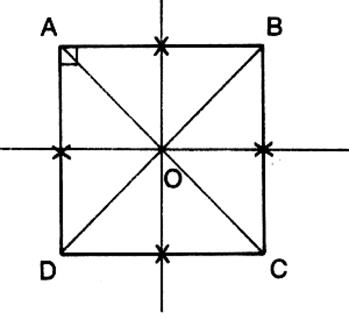
Les droites « delta » et « delta prime » sont les médiatrices des côtés des quadrilatères.

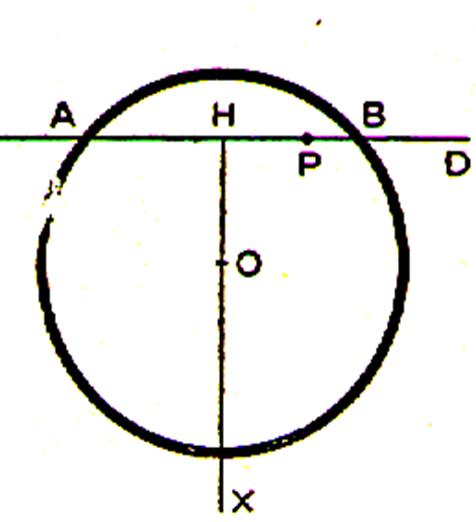
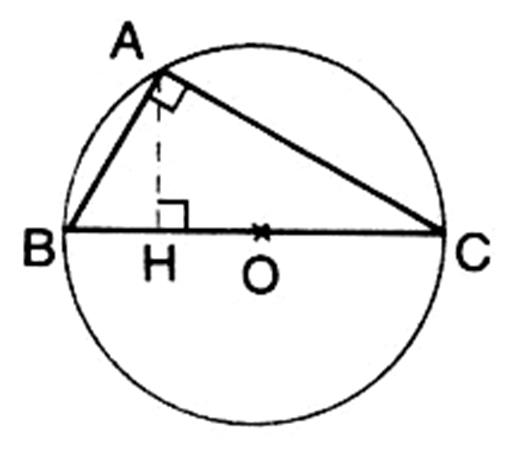
Cas particulier : les médiatrices du triangle rectangle se coupe au point « O ». qui se trouve sur le plus grand côté de ce triangle  ( appelé ; hypoténuse BC )

 

 

 

TRAVAUX AUTO – FORMATIFS .

CONTROLE :

 

1.     Qu’est qu’une médiatrice ?

2.     Quel  nom donne - t - on  aussi à la médiatrice  ? 

3.     Quelles sont les propriétés d’une médiatrice ?

 

EVALUATION

 

1°) Tracer la médiatrice  d'un segment :

a)    avec la règle non graduée et le compas.

b)    Avec la règle graduée et l’équerre.

 

2°) En utilisant les  propriétés  de la médiatrice  , partager le segment AB en 2 puis en quatre parties égales.

 

 

3°)  Tracer un segment AB , tracer la médiatrice  de ce segment , placer un point  M sur la médiatrice , un point   O    en intersection de la médiatrice et du segment .

 Que peut - on dire des angles AMO et  OMB ?

 Que peut-on dire des angles ABM et  BAM ?

 

4°)  Placer 3 points non alignés A , B et C tels que  : AB = 3 cm ; BC = 4 cm  et  = 120° .

Construire la médiatrice du segment AB puis celle du segment BC ; elles se coupent en un point  " I " .

Tracer le cercle de centre "I" et de rayon " I A " .

 

Que constate - t- on ? Justifier la réponse .

 

INTERDISCIPLINARITE