|
|
|
|
Le triangle |
ENVIRONNEMENT du
dossier:
|
|
|
|
|
DOSSIER : LES TRAPEZES
|
|
Activité découverte . |
|
|||||||
|
|
Définition : |
|
|||||||
|
|
Les différents trapèzes |
|
|||||||
|
|
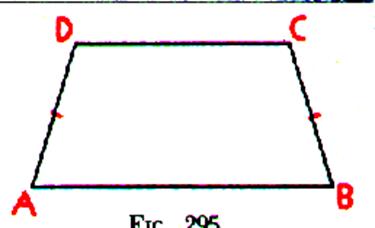
1°)Trapèze quelconque |
|
|||||||
|
|
2°)
Trapèze isocèle ( définition , propriétés ) |
|
|||||||
|
|
3°)
Trapèze rectangle |
|
|||||||
|
|
Info plus : Les propriétés du trapèze isocèle |
|
|||||||
|
|
ET : |
|
|||||||
|
|
Construction d’un trapèze quelconque: |
|
|||||||
|
|
Cas particulier : symétrie et calcul sur les milieux
. |
|
|||||||
|
|
Vérification :
« Base moyenne » |
|
|||||||
|
|
|
|
|||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
TEST |
COURS
|
Interdisciplinarité : |
|
||||||
|
|
|
|
|
|
|||||
|
|
|
|
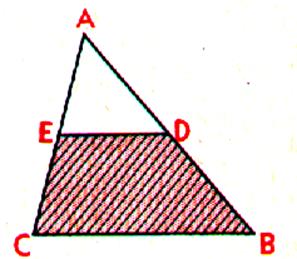
Activité découverte
: Soit un triangle quelconque ABC; si par un
point D du coté AB , nous menons une parallèle DE au coté BC , cette
parallèle détermine un quadrilatère BCED qui a deux cotés parallèles et que
l'on appelle "trapèze" |
|
|
Définition : |
|
|
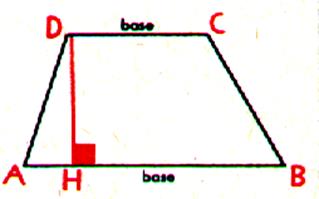
Un trapèze est un quadrilatère qui a deux
cotés parallèles. Les cotés parallèles AB et CD sont les
"bases" du trapèze. La distance DH de ces bases est la hauteur
du trapèze. |
|
|
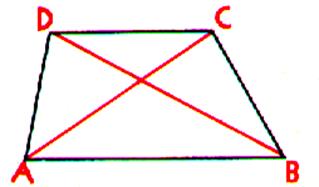
Les diagonales sont les droites AC et BD qui joignent
deux sommets non consécutifs. |
|
Les
3 Différentes sortes de trapèze :
|
1°)Trapèze
quelconque |
|
|
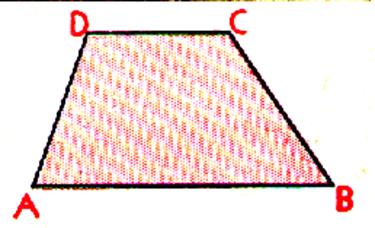
Définition description : - Quadrilatère convexe ayant deux côtés parallèles . [DC] // [AB] - [DC] et [AB]
sont les bases. AB > DC [DC] est la plus petite base et
[AB] est la plus grande base. |
|
|
Propriétés: les angles ayant pour sommets les extrémités
d’un des côtés non parallèles sont supplémentaires .
Identification : Quadrilatère convexe ayant deux côtés
parallèles . [DC] // [AB] |
|
|
2°) Trapèze isocèle |
|
|
Définition , description : C’est un trapèze dont les cotés non parallèles sont isométriques. (1) AD = BC
|
|
|
-Propriétés du trapèze isocèle. - les angles à la base sont égaux -
les médiatrices des bases sont confondues ( 3) -
l’axe de symétrie : médiatrice des bases -
l’identification se fait avec (1) ou
(2) ou (3) |
|
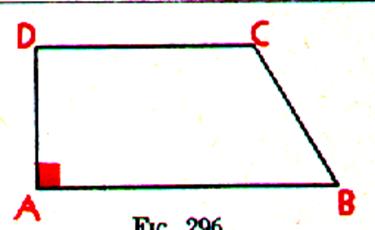
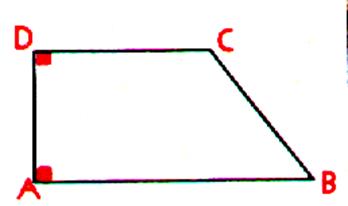
3°) Trapèze rectangle DCBA
|
|
|
Description : Trapèze ayant un angle droit
|
|
|
Propriétés : -
propriétés du trapèze quelconque -
si Identification à
partir de : Trapèze ayant un angle droit |
|
|
INFO
PLUS : sur les propriétés du trapèze isocèle |
|
|
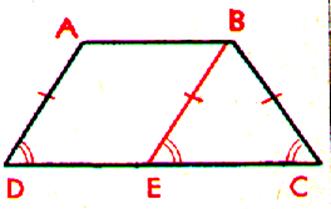
Traçons sur une feuille de calque l’angle CDA ,
nous retournons le calque tel que D soit en C et que DC soit superposé à CD ; nous constatons que l’angle D
et l’angle C sont égaux . Si nous menons en B une parallèle au côté DA ,l’angle D est égal à
l’angle E qui est égal à l’angle
C .Le triangle EBC est isocèle. Et EB et BC sont de même longueur |
|
|
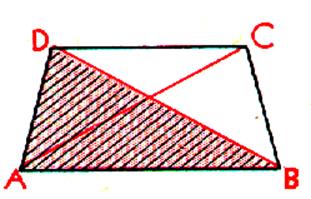
Les
diagonales sont égales :Soient AC et DB les diagonales . Décalquons le
triangle ADB puis retournons le caque de façon que AD se place sur BC ;
A se superpose à B , le triangle ADB se superpose au triangle ACB .
donc : AC = BD
|
|
|
INFO PLUS sur les propriétés du trapèze rectangle : |
|
|
1°)
le trapèze rectangle a deux angles droits : l’angle A = l’angle D = 1droit en effet : AD étant perpendiculaire à AB est aussi
perpendiculaire à DC puisque AB et DC sont parallèles. 2°)la hauteur se confond avec le côté AD |
|
|
Construction d’un trapèze quelconque: |
|
|
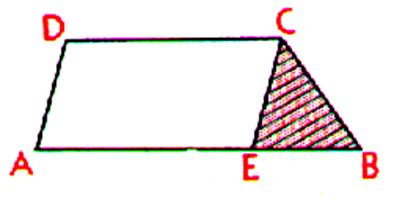
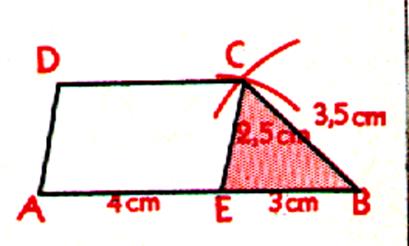
Construire
un trapèze quelconque dont on connaît les 4 côtés : Soit construire un trapèze tel que :*DC = 4 cm ; BC =3,5
cm ; AD = 2,5 cm ; AB = 7cm. Nous remarquons que si le sommet C d’un trapèze quelconque nous menons
une parallèle CE au côté AD , cette
parallèle décompose le trapèze en un parallélogramme AECD
et en un triangle BEC tel que : EB = AB – DC EB = 7 cm – 4 cm = 3cm EC = AD = 2,5 cm et BC = 3,5cm |
|
|
Il nous est donc possible de construire le triangle BEC puisque nous
connaissons ses trois côtés. Pour obtenir ensuite le trapèze , nous prolongeons EB d’une longueur
AE = 4 cm . Par le point A , nous menons une parallèle à EC et par le point C, une parallèle à AE.
L'’intersection D des deux parallèles ainsi obtenues donne le quatrième
sommet du trapèze. |
|
|
Cas particulier : symétrie et calcul sur les milieux
. |
|
|
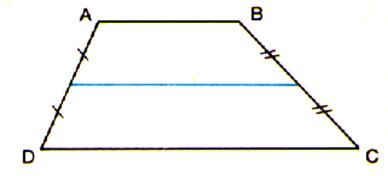
VOIR le « Calcul sur les milieux » Dans un trapèze quelconque l’axe
de symétrie des deux parallèles passe par les milieux des côtés AD et BC et les diagonales AC et B D. Dans tous les trapèzes, la droite portée par cette axe a pour longueur la demi -somme des bases.
(à vérifier).Elle est appelée « base
moyenne » |
|
|
Vérification :
« Base moyenne » |
|
|
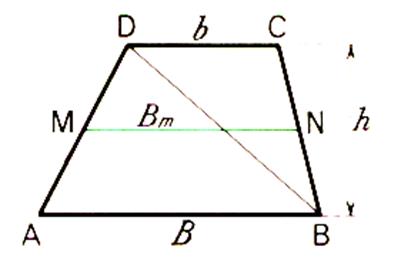
La droite
« milieu » ,
parallèle aux bases , est appelée
« base moyenne » ( B m ) La longueur de la base moyenne est égale à la somme des bases divisée
par 2 : MN = B + b 2 |
|
CONTROLE :
1°) citer les principaux trapèzes .
2°) quelles sont les caractéristiques du trapèze quelconque
3°) quelles sont les caractéristiques du trapèze isocèle
4°) quelles sont les caractéristiques du trapèze rectangle
EVALUATION
Pour Q1 ;Q2 ;Q3 prendre les dimensions que vous voulez !!
1°) Tracer un trapèze quelconque
2°) Tracer un trapèze rectangle
3°) Tracer un trapèze
isocèle
4°) Tracer :
|
a)
Trapèze ABCD de bases AB = 5cm et DC = 2,5 cm de côté AD = 3,5
cm ; et |
|
|
b)
Trapèze ABCD de bases AD = 20 mm et BC = 55 mm de
côté = 35 mm et hauteur AH = 25 mm |
|
|
c)
Trapèze
isocèle ABCD de bases AD = 30 mm et BC
= 50 mm et de côté 25 mm |
|
|
d)
Trapèze isocèle ABCD de bases AD = 46 mm et BC = 20 mm et |
|
|
e) Trapèze rectangle
ABCD : |
|
|
f)
Trapèze rectangle
ABCD : |
|