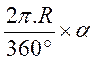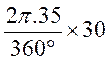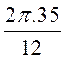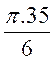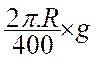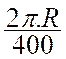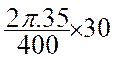Pré
requis:
|
|
ENVIRONNEMENT
du dossier:
|
Objectif
précédent : |
Objectif
suivant : |
||
|
|
|
|
|
|
|
|
|
|
DOSSIER
: Calcul
de la longueur d’un arc
.
( angle au centre exprimé en degré ; grade ou radian)
·
Calcul de la mesure d’un arc.(angle au centre)
·
Longueur d’un arc ( angle
en degré)
·
II )
LONGUEUR D’UN ARC ( angle
en grade)
·
III )
LONGUEUR D’UN ARC ( angle
en radian) :
|
TEST |
COURS
|
Interdisciplinarité : |
|
COURS
Calcul de la mesure
d’ un arc :
|
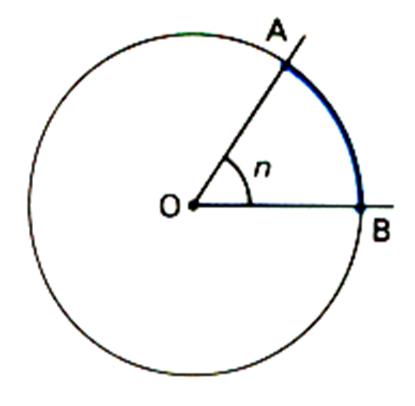
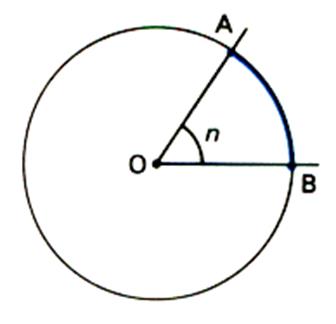
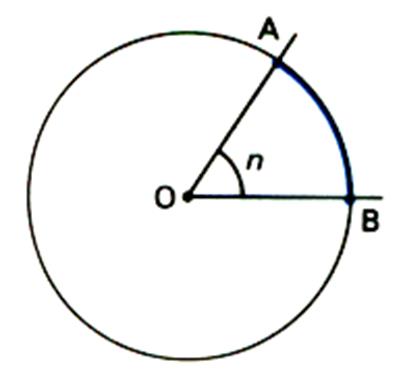
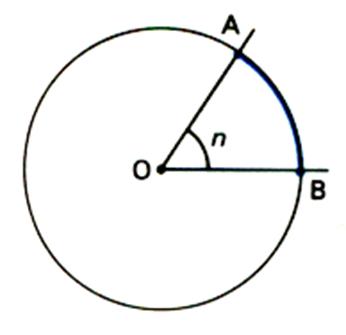
On dit aussi : Calculer la longueur d’un arc de cercle engendré par un angle «
n » , et
de rayon « R ». R = d( O,A) ou d(O,B) « n »
est appelé « angle au centre » |
|
On mesure rarement la longueur d’un arc
Pré requis :Pour calculer la longueur d’un
arc ; il faut savoir calculer la longueur de la circonférence du cercle ( C ) :
|
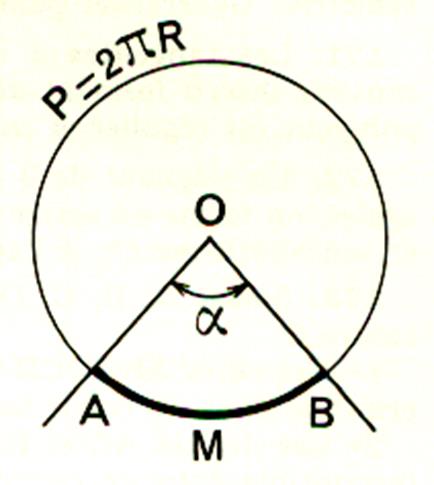
La longueur de
la circonférence du cercle (désigné par : C ou Pd ) est égale
au périmètre du disque "Pd". Pd
= p
D ou 2 p R |
|
LONGUEUR D’UN ARC : ( 3 cas
possibles )
Dans
un cercle donné , la longueur d’un arc est proportionnelle à sa mesure en degré
ou en grades .
I ) LONGUEUR
D’UN ARC ( angle en
degré) :
|
Pré requis ; :le
degré et le système sexagésimal :
Système sexagésimal |
Le cercle est divisé en 360 arcs égaux , chacun de ces arcs est appelé « degré-
arc » ; le degré – arc est donc la 360e partie du cercle .
Le degré – arc ( ° )
est l’unité d’arc dans le système sexagésimal .
Sous multiple de « degré – arc » .
La minute – arc ( ’ ) est la 60e partie du degré – arc ;
La second – arc ( ’’ ) est la 60e partie de la minute – arc ;
Les opérations sur les nombres qui mesurent
les arcs en degré , minutes , secondes s’effectuent
suivant des règles particulières .(Voir : INFO plus)
|
Calcul de la longueur d’un
arc de cercle dont l’angle est exprimé en degrés : ( a °) |
|
|
Formule : lg arc = |
On
divise le périmètre du cercle en 360 parties égales ; pour multiplier
par le nombre degrés de l’angle
au centre de l’arc. |
|
Si l’angle alpha( On
sait que lg arc = soit :
lg arc = |
|
Voir :
Aire du secteur circulaire
On obtient la
longueur d’un arc en multipliant la longueur de la circonférence par le nombre
de degrés de l’arc et en divisant le produit par 360.
II ) LONGUEUR
D’UN ARC ( angle en
grade) :
Pré
requis : le grade et le système décimal
|
Le système décimal |
Le
cercle est divisé en 400 arcs égaux ; chacun de ces arcs est appelé
« grade -arc » ; le grade-
arc est donc la 400e partie
du cercle
Le
grade – arc , en abrégé : gr , est l’unité d’arc
dans le système décimal.
Sous
multiple du « grade – arc » :
Le
décigrade- arc ,
en abrégé : dgr est égal à 0,1 grade – arc
Le
centigrade- arc ,
en abrégé : cgr est égal à 0,01 grade – arc
Le
milligrade- arc ,
en abrégé : mgr est égal à 0,001 grade – arc
Les
opérations sur les nombres qui mesurent les arcs en grades ,
décigrades , milligrades sont les mêmes que les opérations sur les nombres
décimaux.
|
Calcul de la
longueur d’un arc de cercle dont l’angle est exprimé en grades :
( g ) |
|
|
Formule :
lg arc = |
On divise le périmètre du cercle en 400 parties égales ; pour
multiplier par le nombre grades de l’angle au centre
de l’arc. |
|
Si
l’angle alpha( On sait que lg arc de soit : lg arc de g
(grades) = si R = |
|
Voir : Aire
du secteur circulaire
On
obtient la longueur d’un arc en multipliant la longueur de la circonférence par
le nombre de degrés de l’arc et en divisant le produit par 360.
III ) LONGUEUR
D’UN ARC ( angle en radian) :
Pré
requis : le grade et le système décimal
|
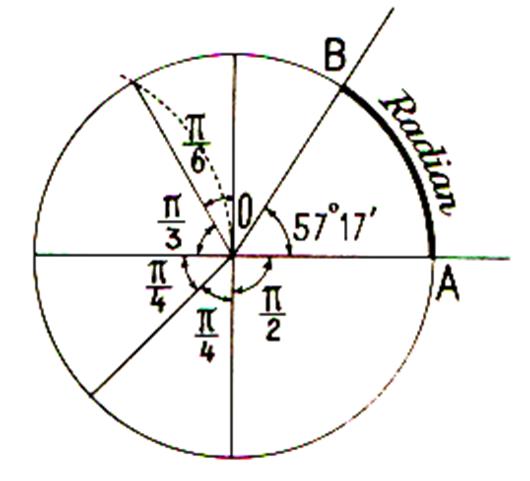
Mesure d’arc en radians |
|
|
Le radian , en abrégé : rd , est l’arc
dont la longueur est égale au rayon du cercle auquel il appartient . Cette unité est l’unité légale
d’arc |
|
Calcul de la longueur d’un arc de cercle dont l’angle est exprimé en radian : ( w
) (w lire « oméga » » ) |
|
|
Théorème : la longueur d’un
arc de cercle est égale au produit de son rayon par sa mesure en radian . |
|
|
La longueur d’un arc de 1 rad est R . Celle
d’un arc de w rad est donc Rw :
l = Rw En particulier , dans un cercle de rayon 1 , la longueur d’un
arc est égale à sa mesure en radians . |
|
TRAVAUX AUTO _ FORMATIFS
1°) Donner la définition d’un « angle au
centre :
Un angle au centre est un angle qui a son sommet au centre d’un cercle .
2°) Le cercle est divisé en 400 arcs égaux ; chacun de ces arcs est
appelé « grade -arc » ; le
grade- arc est donc la 400e
partie du cercle