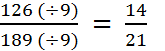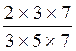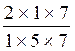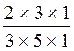Pré requis:
|
|
|
|
|
|
|
|
|
|
Vue en classe de 6éme
|
|
1°)
Fractions égales et simplifiées(CM) |
Fraction irréductible |
Arithmétique :
sur la fraction… |
DOSSIER : FRACTION :« SIMPLIFICATION »
|
Interdisciplinarité
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Simplification d’une fraction:
Par définition : Simplifier une fraction c’est
diviser le numérateur et le dénominateur par une même nombre non nul.
Procédure pour simplifier une fraction:
I ) Décomposer les nombres en produit de facteur.
Si « a » (numérateur) et
« b » (dénominateur) sont des nombres composés (voir NP3) ,nous
pouvons décomposer le numérateur et le dénominateur en produits de facteurs
premiers (SOS Cours).(Les facteurs communs sont des
diviseurs communs ).
II)
Supprimer* un facteur commun.
Il suffit de supprimer, dans la
décomposition en produit de facteurs premiers du numérateur et du dénominateur,
un facteur commun ,
III )
Recalculer le numérateur et le dénominateur.
ensuite de recalculer le nouveau
numérateur et dénominateur ,on obtient une nouvelle fraction égale à celle
d’origine.
(* « supprimer
un facteur commun »:cela revient a neutraliser ce facteur commun en le
remplaçant par 1)
Exemple
d ‘ Application: .
Simplifier 
Résolution :
I )on
décompose 42 et 105
42 = 2 x 3 x
7
105 = 3 x 5 x 7
ce qui donne:
= 
= (nous
avons deux solutions de simplification)
II) On supprime* un facteur commun:
(* « supprimer un facteur commun »:cela revient
a neutraliser ce facteur commun en le remplaçant par 1)
soit =
=
=
(ici le
facteur commun « choisi »est 3
) ou =
=
= 
(ici le
facteur commun choisi est 7)
III ) On propose une solution: ou
Si aucune consigne n ’apparaît
, on propose la solution qui nous
convient.
Cas où la Simplification
est évidente :
Certaines simplification
peuvent paraître évidentes ,notamment lorsque l’on connaît les caractères de divisibilité.
par
exemple : simplifier la fraction 
;
dans ce cas certaines simplifications
sont évidentes puisque 12 et 36 sont divisibles par deux et par trois , deux réponses immédiates sont
possibles:
;
;...d’autres en découlent
Il en est de
même pour une fraction du type : 
où l’on
remarque la simplification évidente
telle :
Activités : Simplifier directement les fractions
suivantes
|
Soit la fraction : |
On peut diviser le numérateur et le dénominateur par : |
Proposition de réponse : |
|
|
Par 3 |
3/2 (elle
est aussi rendu irréductible) |
|
|
par 2 pour
simplifier ou par 4
pour rendre irréductible . |
4/6 |
|
|
par
2 ; 5 ;10 ;
25 ; 50 |
5/10 |
TRAVAUX AUTO FORMATIFS.
Rappels:
Donnez la définition d’une fraction
(caractéristiques).
Donnez la
définition d’un rationnel.
Donnez la définition d’une écriture fractionnaire.
|
Fin du rappel: |
Eventuellement : SOS cours |
1°)
Compléter la phrase:
une fraction
est réductible si on peut la
...……........;mais on ne peut pas .………………............(même mot) une fraction
irréductible.
Que veut dire « simplifier une fraction »
?
2°) Que
faut-il faire pour réduire (ou simplifier une fraction)?
3°) Donner
la procédure permettant de simplifier une fraction .
4°) Pour « supprimer un facteur
commun »,comment procède-t-on ?
1°) Quel différence y a t - il entre ces deux
écritures 
et 
?
2° ) Comment appelle-t-on cette écriture
mathématique 
et (nommez tous
les éléments qui la composent) ?
3°) Simplifier directement les fractions suivantes:
; 
; 
5°) Simplifier les fractions suivantes: 
; 
;
; 
;
;
;
;
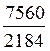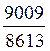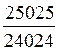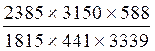
