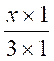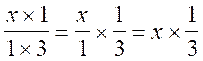|
DOC : formation individualisée soutien en ligne. |
DOC : livre Elève
.Cours interactifs - et travaux + corrigés. |
DOSSIER (1/5) : LES EGALITES Nomenclature 1
|
DOSSIER N°4-A : INTERACTIF |
Information
« TRAVAUX » |
|
OBJECTIFS : - Savoir définir ; identifier et reconnaître : un terme , un facteur , un
facteur commun |
I ) Pré requis:
|
Lecture :
les conventions d’écriture en algèbre : coefficient ; lettres ;…. |
|
|
|
II ) ENVIRONNEMENT du dossier :
|
Objectif précédent : |
Objectif suivant : |
III ) LECON n° 4-A
:
DOSSIER (1/5) : les
égalités : Nomenclature 1 -Vocabulaire
Chapitres :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IV) INFORMATIONS « formation leçon » :
|
|
|
|
Corrigé des travaux
auto - formation. |
||||
|
|
|||||||
V ) DEVOIRS ( écrits):
|
Devoir diagnostique L tests. |
Ÿ |
|
Ÿ |
|
|
Devoir Formatif « Contrôle :
savoir » ; ( remédiation) |
Ÿ |
|
Ÿ |
|
|
Devoir sommatif . |
Ÿ |
|
Devoir certificatif : ( remédiation ) |
Ÿ |
* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .
|
Leçon |
Titre |
|
N°1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
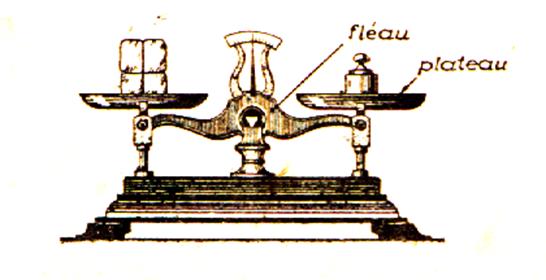
L’appareil
utilisé pour faire penser à
l’égalité est la balance Roberval. L’aiguille est à zéro ; Les plateaux sont
équilibrés. La balance est en équilibre lorsque « Ce qu
‘il a sur le plateau de droite est égal à ce qu’il y a sur la plateau
de gauche. » |
|
A PROPOS Du mot
« TRADUIRE » en langage littéral , ou
traduire en langage symbolique mathématique :
Tout
ce qui est « exprimé » peut
être traduit dans différentes formes .(
écrite , orale , ou objet « fabriqué » ( manufacturé , peinture , sculpture ) ces traductions visent à transmettre des
informations .
En mathématique ,
en cours magistral , on passe facilement
d’un langage oral au langage écrit .
Ce langage graphique « écrit »
utilise deux autres formes d’écriture complémentaires ( le dessin codifié
et des « signes » ou de « symboles » ) :
- dessin : pour éviter l’écriture de textes trop
longs; il est utilisé « le dessin », on parle souvent de
« représentations graphiques ».
Les
connaissances de bases en géométrie sont importantes ,elles
codifient les points et leur
position ; les traits et leurs
positions ; …..
Toutes les écritures utilisent des symboles :
Comme dans la langue
écrite pour communiquer ( en français
par exemple ) on utilise des signes que
l’on nomme « Les
alphabets » : utilisation de
l’alphabet (grec , latine ) en complément
de notre langue « locale » («le français » pour les
français , «l’ anglais » pour les anglais , «le chinois »
pour les gens de ce pays )
Il en est de même en
mathématiques :
On apprend d’ abord à connaître
, reconnaître , dessiner et
nommer les signes numériques (les chiffres), et opératoires …. ( signes tels que
: ; + ; / ; ….)
Pour
communiquer en mathématique
, il est très souvent demandé de passer d’une forme d’expression à une autre.
Exemple : on écrit « parallèle » on
dessine « // » qui signifie
« parallèle ».
IL faut donc savoir
passer d’un langage littéral à un langage
mathématique et vis et
versa :
On considérera que ce qui est traduit en langage littéral est ce qui peut s’écrire avec des mots (des
lettres ou des noms).
On considérera que ce qui est traduit en langage mathématique est ce qui peut s’écrire avec des symboles
mathématiques (lettres ,
signes ;chiffres ;......).
Dans tous les cas il faut savoir décrypter et traduire et passer d’une
forme à l’autre.
On
peut passer successivement d’un modèle à l’autre :
Couramment
dans un problème mathématique
doit savoir passer d’une équation , à un tableau numérique , à une représentation
graphique dans un repère et vis versa .
Parfois le
problème est posé à partir d’un texte , d’une équation ; d’ un tableau numérique ou avec une représentation graphique dans un
repère. Il faut souvent savoir passer de l’un à l’autre ,
parce qu’il faut répondre aux questions posées.
|
|
|
Le signe de reconnaissance de
l’égalité est le symbole :
« = »
Ce qui est incontestable : ce qu’il y a « à
droite » du signe est égale à ce qu’il y a « à gauche » du signe
égal .
En sciences : l’égalité
est représentée par la balance de Roberval . Après l’, équilibrage des plateaux ( les plateaux sont horizontaux ,
l’aiguille réglée au « zéro ») la balance Roberval est l’image type de
l’égalité dans un partage.
On dit que ,
ce qu’il y a sur le plateau de gauche est égal en masse à ce qu’il y a sur le
plateau de droite.
Construction de ce symbole: le symbole de l’égalité est le
tracé de deux traits forts ,parallèles ,et parallèle a la ligne d’écriture,
d’environ 3 mm de longueur.
C’est le signe le plus utilisé !
Quand
ce n’est pas égal : on dit « inégal » le symbole est :¹ ;
c’est ensuite que l’on peut effectuer un
classement , en ordre. ! ! !,
alors que l’ on a pas trouvé l’égalité .
Attention : les expressions algébriques sont des
simplifications ( écriture simplifiée ) des sommes
algébriques ; il est donc impératif de savoir transformer les expressions
algébriques en somme algébrique avant de rechercher à identifier , les termes .
|
|
|
Souvenir :
On a apprit en calcul numérique qu’une addition contient des
termes ; que les deux termes d’une fractions sont appelés l’un «numérateur » l’autre
« dénominateur ».
Ici : Nous sommes en algèbre : nous
devons nous souvenir que par définition : le terme est le produit de un ou
plusieurs facteurs.
En algèbre : une suite de termes constitue ce que l’on appelle : une expression algébrique.
Règle d’or à appliquer :
Toutes les
expressions algébriques sont les simplifications d’une somme
algébrique.
(@) ; pour identifier sans erreurs « les
termes » il faut savoir transformer chaque expression algébrique en somme
algébrique .
Dans une expression
algébrique : On appelle
« terme » un nombre
(précédé ou non d’un signe opératoire )
(exemples : 5 ;
35,7 ; … ; + 8,2 - 790 ;…….) , ou un nombre associé à une ou plusieurs lettres (avec ou sans exposant) ( exemple : 3 ab ; 4 d b² ;… ; + 7x
; - 6 by² …) , ou une ou des
lettres( x² ; xy² ; … ; - x ; - a x² ….) ;
Mais pour les identifier sans
erreur on transformera toutes les « expressions algébriques » en
« sommes
algébriques .», tous les termes
sont alors contenus dans des parenthèses , on dit que chaque terme est situé à gauche ou et à droite du signe opératoire
+ ; dans la somme
algébrique.
On dit aussi :on appelle « terme algébrique » une expression
formée d’une ou plusieurs lettres , ayant ou non un coefficient , et qui ne
sont séparées par aucun signe + ou - ; le signe + ou – précédent ( devant
)cette expression appartient au terme.
Exemples
de termes algébriques
« simplifiés » : 4 ; + 5 ; - 7 ; 3a ; 4,5 x
; abc ; 6 x2 ;
Que l’on devrait
écrire :
4
s’écrit (+4) ; + 5
s’écrit ( +5) ; - 7 s’écrit ( -7)
; 3a s’écrit ( +3a) ; 4,5 x
s’écrit ( + 4,5 x ) ; abc s’ écrit
( + abc) et 6 x2
s’écrit ( + 6x²) ;
mais
aussi ( +3 ) ; ( +5x ) ;
( +4x²) ; ( - 3 ) ; (
- 5x ) ; ( - 4x²) sont des termes . » écrits non
simplifiés
Commentaire: Une somme algébrique n’est qu’une suite d’additions
de termes positifs ou
négatifs ; on dit aussi que Dans la
somme algébrique le signe de l’addition ( + ) séparent des « termes »
Exemple
1 :
soit l’expression algébrique : +3
+5x +4x² ; devient la somme algébrique (
+3) + ( +5x ) + ( +4x²) ; qui comprend les trois termes : (
+3) ; ( +5x ) ; ( +4x²) ; ( constat : les 3 termes sont
positifs)
Exemple
2 :
soit l’expression algébrique : - 3
+5x - 4x² ; devient la somme algébrique (
-3 ) + ( +5x ) + ( - 4x²) ; qui comprend les trois termes : (
- 3) ; ( +5x ) ; ( - 4x²) ; ( un terme est positif , les 2 autres sont négattifs)
Exemple
3 :
soit l’expression algébrique : - 3
- 5x - 4x² ; devient la somme algébrique (
-3 ) + ( - 5x ) + ( - 4x²) ; qui comprend les trois termes : (
- 3) ; ( - 5x ) ; ( - 4x²) ; ( constat : les 3 termes
sont négatifs )
Attention :
par définition ,le signe de la soustraction
ne peut pas séparer les termes ; puisque nous devons
transformer les expressions algébrique
en une somme algébrique pour identifier les termes.
impératif !
: toute expression numérique ou algébrique doit être transformée en
« somme algébrique ».avant de
nommer les termes.
Exemples :
|
Expression algébrique |
Transformation
en somme algébrique |
Terme
n°1 |
|
Terme
n°2 |
|
2
+ 7 |
+
(+2) + (+7) |
(+2) |
|
(+7) |
|
2
- 7 |
+
(+2) + (-7) |
(+2) |
|
(-7) |
|
(+5)
+ (+8) |
|
(+5) |
|
(+8) |
|
(+4 ) - (+3) |
+
(+4 ) + ( - (-3)) |
(+4) |
|
(
- (-3)) |
|
3 +
15,5 |
+
(+3) + (+15,5) |
(+3) |
|
(+15.5) |
|
x +
5 |
+
(+ x ) + ( +5 ) |
(
+ x) |
|
(+5) |
|
-
|
+
(- |
(-
|
|
(+ 7) |
|
2x -3 |
+
(+2x) + (-3) |
(+2x) |
|
(-3) |
|
(a ) + (+ b) |
+
(+ a ) + (+
b) |
(a ) |
|
(+
b) |
|
(+
x²) + (+3x) |
|
(+
x²) |
|
(+3x) |
|
(
.....) + (........) |
|
(
.....) |
|
(........) |
Autre
exemple
|
expression |
transformation |
1er
terme |
2
éme terme |
3èmeterme : |
|
-2x²
+3x -5 |
(-2x²)
+(+3x) + (-5) |
(-2x²) |
(+3x) |
(-5) |
|
|
|
Définition :
les
nombres ou lettres situés à gauche et ou à
droite du signe « multiplier » s’appellent des
« facteurs ».
Attention : par convention et pour ne pas confondre la lettre
« x » et le signe
« x » (multiplier ) , en algèbre le signe
« multiplier » n’est pas dessiné ,
|
38 est un nombre |
ab est la
multiplication « a fois
b » |
|
|
|
38a est la
multiplication : 38 fois a |
2a est la multiplication « 2 fois a » |
|
|
|
2x est la multiplication :2 fois ixe |
2ab est la
double multiplication : 2 fois « a » fois « b » |
|
|
*Dans
le cas de la division (ou fraction) il faudra « passer » par la « multiplication par l’inverse »
exemple 
devient
;
soit
« x » multiplié par 1/3
|
Termes |
facteur1 |
facteur2 |
facteur3 |
facteur(n) |
||||
|
3
|
3 |
7 |
|
|
||||
|
(+3) ( +7) |
(
+ 3 ) |
(
+ 7 ) |
|
|
||||
|
a b |
a |
b |
|
|
||||
|
3 x |
3 |
x1 |
|
|
||||
|
xy |
x1 |
y1 |
|
|
||||
|
-3
x devient |
-3 |
x |
|
|
||||
|
(-2)
² devient (-2)
(-2) devient (-2)1
(-2)2 |
(
- 2 )1 |
(-2)2 |
|
|
||||
|
- 2²
devient - ( +2) ( +2) devient - ( +2)1 ( +2)2 |
-
( + 2 )1 |
(
+2)2 |
|
|
||||
|
3x2 devient 31 x1 x2 |
31 |
x1 |
x2 |
|
||||
|
* devient : x1inv.3 |
x1 |
|
|
|
||||
|
(x+2 ) ( x-3 ) |
(x+2 ) |
(
x-3 ) |
|
|
||||
|
Autres exemples : |
||||||||
|
3
|
3 |
|
|
|
||||
|
3x2
/7 devient 31x1x2
/ 71 |
31 |
x1 |
x2 |
inv.
71 |
||||
|
-10x2 devient : -21
51 x1 x2 |
-21 |
51 |
x1 |
x2 |
||||
REMARQUE : Les facteurs d’une décomposition sont
« indicés » pour permettre de les identifier .
A
) (x+2 ) ( x-3 )
lire
( x +2 ) fois ( x- 3) donc (x+2) est
un facteur ; et (x-3) est
un facteur.
B ) 3 
lire
3
fois (lire aussi : « que
multiplie ») « racine
carrée » de 7 ; donc 3
est facteur et est un
facteur.
Soit le Produit = facteur facteur
(.....) (........) = (.....) fois (.........)
Remarquer qu ‘ entre deux parenthèses le signe
« multiplier» disparaît
REMARQUE :
Les facteurs d’une décomposition seront
« indicés » afin de les identifier .
|
|
|
Un terme est composé de un
ou plusieurs facteurs
exemple: soit
l’expression ab +3x + y - 7
qui
devient la somme algébrique : + (
+ab) + (+3x ) + ( + y ) + ( - 7 )
( +ab) est un terme composé des facteurs
« a » et
« b »
(+3x ) est un
terme composé des facteurs « 3 » et « ixe »
( + y ) est ,à la fois, un terme et un
facteur ( « y » fois
1)
( - 7 ) est , à la fois ,un terme et un
facteur (-7 fois 1 )
On
admettra que tout nombre ou lettre
isolé (exemple « +y » et
«- 7 »)sont des termes et deviennent des
facteurs si on les multiplie par l’élément neutre 1.
|
|
Traduction en langage mathématique et littéral et vis versa |
|
On considérera que ce qui traduit en langage littéral est ce qui peut s’écrire avec des mots (des
lettres ou des noms) ou qui peut se dire
oralement.
Dans tous les cas il faut savoir décrypter ,traduire
soit une forme soit sous une autre.
(littérale ou
mathématique).
I)
Passage de la forme littérale à la forme mathématique
|
Forme
littérale : |
Forme
mathématique |
|
1°) « a » facteur « b » égal « c » |
a b
= c |
|
2°)
« a » moins « b »
plus « c » facteur « d » |
a - b + c d |
pour utiliser le mot
« terme » il faut transformer l’expression en somme algébrique.
II)Passage de la forme mathématique en langage littéral:
forme mathématique: forme littérale:
a - b = c d + f - g « a »
moins « b » est égal à « c » facteur
« d » plus « f
» moins « g »
pour
utiliser le mot « terme » il faut transformer l’expression en somme
algébrique.
+ (+a) + ( -
b) = + (+ c d ) + ( + f ) + (- g)
ainsi on
pourra lire : le
terme plus « a » plus le terme moins « b » est égal au
terme plu « c » facteur « d » plus le terme plus
« f » plus le terme moins « g »
|
|
|
Il faut au
minimum deux termes ,et il peut y avoir un ou plusieurs facteurs communs).
Si
dans deux termes ,
nous avons des facteurs identiques nous
dirons que les termes on des « facteurs communs ».
REMARQUE : Les facteurs d’une décomposition sont « indicés »
pour permettre de les identifier .
*Savoir rechercher les facteurs communs à deux ou
plusieurs termes est indispensable pour savoir
« factoriser ,développer », calculer
un PGCD ; rendre irréductible une fraction.
Il faut au minimum
deux termes pour rechercher un facteur commun ( à ces deux termes)
Exemples: Recherche des facteurs communs
Pour
rechercher des facteurs communs dans une expression algébrique ; il
faut :
transformer
l’expression algébrique en somme algébrique ensuite identifier les termes ,
dans les termes il faut décomposer les termes en produit de facteurs ( les
indicer) ,et identifier les facteurs communs de même indice .
(voir le tableau ci
dessous)
|
expression alg. |
somme alg. |
Terme(s) |
facteur(s) |
facteur(s ) commun(s) |
|
3x +
2x |
(+3x) + (+2x) |
(+3x) (+2x) |
+31 ;x1 21 ; x1 |
x1 |
|
3x
+ 3y |
(+3x)
+ (+3y) |
(+3x) (+3y) |
+31 ;x1 +31 ;y1 |
+31 |
|
3x + 3 |
(+3x)
+ (+3) |
(+3x) (+3) |
+31 ; x1 +31 |
+31 |
|
x² -
2x |
(+x²)
+ ( - 2x) |
(+
x²) ou(+x1x2) (
- 2x1) |
x1 ;
x2 -21 ; x1 |
x1 |
|
-3x² + 6 x |
(-3x²) + ( +6 x ) |
(-3x²) et (
+6 x ) |
- ;3; x1 ;x2 + ; 2 ; 3; x1 |
3x |
|
(
x +1 ) ( x-3) + ( x + 1 ) ( x +
2) |
[( x +1 )
( x-3)] +[(
x + 1 ) ( x + 2)] |
[( x +1 )1
( x-3)1] [( x + 1)1 ( x + 2)1] |
(
x +1 )1 ; ( x-3)1 (
x + 1)1 ; ( x + 2)1 |
(
x +1 )1 |
|
(-3) (+7) |
(-3) (+7) |
(-3) ; (+7) |
|
impossible |
|
2
|
(2 |
(2 |
21;
31 ;
|
|
|
a- b |
+ (+a) + ( -b) |
(+a) + ( -b) |
(+a) ; ( -b) |
aucun |
|
3 |
* |
|
|
|
|
*remarque ( |
|
)
(
voir la leçon sue les .racines N ( travail
personnel ; voir les travaux auto formatifs)