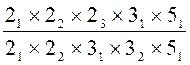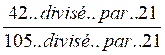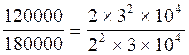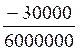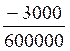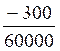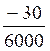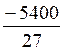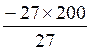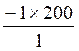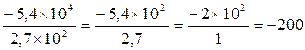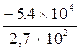Pré
requis:
|
Sciences : simplification de fraction et
« irréductible » |
|||
|
Fraction : nomenclature |
|||
|
Calcul du PGCD |
|
||
|
Nombres premiers entre eux |
|
||
ENVIRONNEMENT du dossier :
|
|
|
|
Vue en de CLASSE
: 6éme |
|
Objectif
précédent : |
Objectif
suivant : 2°) la Fraction représentant un nombre décimal |
DOSSIER : Rendre une FRACTION IRREDUCTIBLE
|
|
|
|
|
|
|
|
|
|
COURS
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Par définition:
Une fraction est dite
« irréductible » si le numérateur et le dénominateur sont premiers
entre eux .
(Rappel info @ l :deux nombres sont
premiers entre eux si leur PGCD est égal
à 1)
Remarque : Il y a plusieurs procédures (méthodes)
permettant de rendre irréductible une fraction :
Méthode1:
|
procédure |
Exemple : rendre irréductible la fraction : |
|
1°) décomposer le numérateur en produit de
facteurs premiers. |
120= 2 x2
x 2 x3 x 5 120= 21x22x23x31x51 |
|
2°) décomposer le dénominateur en produit de
facteurs premiers. Indicer les facteurs identiques |
180 = 21x22x31x32x51 |
|
3°) reposer l'égalité |
|
|
|
|
|
5°) rendre compte |
|
Remarque : on pourrait remplacer les facteurs
communs de même indice par "1"
=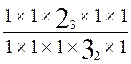 reste 23 en numérateur et 32 en dénominateur
reste 23 en numérateur et 32 en dénominateur
*Cas
particulier : cas où il n'y aurait plus de nombres au numérateur :
exemple : on veut rendre irréductible la fraction ![]()
 attention si au numérateur (ou
au dénominateur )tous les facteurs communs de même indice s’annulent , les facteurs disparaissent mais il faut mettre l’élément neutre 1 en numérateur; tel que :
attention si au numérateur (ou
au dénominateur )tous les facteurs communs de même indice s’annulent , les facteurs disparaissent mais il faut mettre l’élément neutre 1 en numérateur; tel que :
![]() =
= 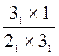 =
=![]()
Méthode 2:
pour rendre une fraction irréductible il suffit
de diviser le numérateur et le dénominateur par leur PGCD.
Commentaire : il faut calculer
le PGCD des deux nombres ; cela revient à calculer le plus petit commun
multiple de deux nombres
|
Procédure : |
Exemple : rendre irréductible la fraction |
|
I ) Décomposer le numérateur et le dénominateur en
produit de facteurs premiers et chercher le PGCD de ces deux nombres. |
I ) On calcule le PGCD de 42 et 105:
...on trouve
21 |
|
II ) Diviser le
numérateur et le dénominateur par leur
PGCD |
II ) on divise le numérateur et le dénominateur par leur PGCD par 21: ce qui donne: 42 : 21 = 2 105 : 21 = 5 |
|
III) On exprime le résultat : |
III ) Résultat : |
|
IV ) Conclusion |
IV ) |
|
V)
Vérification: |
V) Faire le produit en croix de
Calcul de 42 fois 5 = 210 Calcul de 105 fois 2 =210 Les résultats étant identique on peut conclure
que "les fractions sont équivalentes" |
Pour confirmer "l'irréductibilité" il
faut :
On sait que : une fraction est dite «
irréductible » si le numérateur et le dénominateur sont premier entre eux.
;On sait aussi que deux nombres sont « premiers
entre eux » si leur PGCD vaut 1
.
|
On doit faire
le PGCD de la nouvelle fraction trouvée ( 2/5) Ainsi , on calcule le PGCD de 2 et 5 :
le PGCD de deux et cinq vaut
« 1 »
,on peut donc confirmer
et conclure que la fraction |
METHODE 3 :
Procédure permettant de rendre irréductible une
fraction:
Pratiquement (pour aller plus vite)
Enoncé type: rendre irréductible la fraction
![]()
Résolution type:
I) Décomposer le numérateur et le dénominateur en produit de facteurs
premiers.
on décompose 42 et 105
(42 = 2 x 3 x 7 et 105 = 3 x 5 x
7)
ce qui donne:
II)Remettre
les produits sous forme fractionnaire:
Ecriture fractionnaire:
![]() =
= 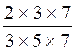
III )Barrer les facteurs communs (autant dans l’un que dans l’autre ,ceux
ayant même indice)
On
barre tous les facteurs communs (ayant
même indice):(cela
revient a les remplacer par l’élément neutre de la
multiplication 1 ).
![]()
![]()
![]()
![]()
![]() =
=![]()
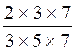 =
=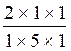 (il nous reste en
numérateur 2 et en dénominateur 5)
(il nous reste en
numérateur 2 et en dénominateur 5)
IV) Exprimer le résultat:
Résultat: ![]() =
= ![]()
AUTRES EXEMPLES :
(il faut passer par les « puissances de
dix » pour aller plus vite ;
si L’objectif Puissance 1 à été
fait ;ensuite voir « puissance
2 » cas « puissance d’une
fraction » ;
Exemple :
Rendre irréductible
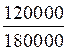 =
=
Plusieurs solutions sont
possibles :
a) Première solution : la plus rapide : « il
suffit de barrer autant de zéros en haut
et en bas ».
|
|
|
b) Deuxième
solution : "on
passe " par les puissances de dix » ;
cela donne pour :
|
1°) |
|
|
2°) |
180000 = 2 |
|
3°) |
120000 = 22 |
|
4°) ce qui donne la fraction écrite |
|
|
|
|
Autres exercices résolus :
|
|
|
|
|
|
|
B) rendre irréductible :
|
|
|
|
|
|
Autres façons de traiter les deux exercices
précédents ( voir Objectif
puissance 3) |
|
|
A ) |
|
|
B) |
|
Rendre irréductible:
|
|
Résultat: |
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS.
1.
Que signifie
l’expression « fraction réductible »?
2.
Que veut dire « rendre irréductible une
fraction »?
3.
Quelle est la procédure qui permet de rendre
irréductible une fraction?
4.
A quelle condition dit-on que la fraction est
irréductible?
1°) Rendre
irréductible les fractions suivantes:
(On dit aussi : Rendre les fractions suivantes irréductibles):
|
|
|
|
|
|
|
|
|
2°)
Simplifier jusqu’à rendre irréductible les fractions suivantes:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
Réduire : (en dernier lieu faire le calcul )
|
|
|
|
|
|
Calcul Algébrique :
Rendre
irréductible les expressions suivantes :
|
|
Réponses |
|
|
|
|
|
|
(Voir document personnel pour autres exercices)