Pré requis:

POINT LIGNE PLAN .
Pré requis : Travaux niveau VI et V

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent : 1°) Les polygones (sommaire) 2°) Polygones : caractéristiques numériques .

Objectif suivant 1°)Les polygones irréguliers 2°) Retour à « polygones informations »

tableau Polygones ( 3 ) Suite : 1°) Les polygones étoilés et des tracés de ROSACES

DOSSIER :

Les tracés des POLYGONES REGULIERS:

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité les polyèdres

Corrigé Contrôle

Corrigé évaluation

Liste des polygones réguliers sont :

En cliquant sur les mots vous avez accès à de plus amples informations sur la figure :

I ) Les polygones de 3 cotés
		Le triangle équilatéral
II )Les polygones de 4 cotés
			Le carré
III ) Les polygones réguliers de plus de 4 cotés
	1. Le pentagone		(5 cotés)
	2. L’hexagone		(6 cotés)
	3. L’ heptagone		( 7 cotés)
	4. L’octogone		( 8 cotés)
	5. L’ennéagone		( 9 cotés)
	6. Le décagone		( 10 cotés)
	Le dodécagone		(12 côtés)
IV ) Les polygones irréguliers de plus de 4 cotés

Quant aux autres polygones réguliers , pour éviter l'emploi de termes techniques trop "prétentieux" , on les désigne par le nombre de leurs cotés.

Ainsi l'on dit : un polygone à 7 cotés , un polygone à 11 cotés , un polygone de 15 cotés,…etc.

Un triangle se désigne par trois lettres , un quadrilatère par quatre lettres , et un polygone quelconque par autant de lettres qu'il renferme d'angles.

Il y a dans un polygone régulier autant d'angles qu'il y a de cotés.

( voir les axes de symétrie dans les polygones réguliers)

Il y a les polygones réguliers et irréguliers :

Pour le traçage des polygones irréguliers le problème est uniquement posé lorsque l’on procède à l’arpentage d’un terrain .

On appelle "polygone régulier" les polygones qui ne remplissent que ces deux conditions : ils ont leurs angles et cotés égaux

Pour dessiner un polygone régulier il est commode de tracer le cercle dans lequel il sera « inscrit » ; c’est d’ailleurs une façon de diviser la circonférence en parties égales .

Nous proposons la CONSTRUCTION des POLYGONES REGULIERS:

Pour construire un polygone il faut décrire une circonférence que l'on partage en autant de parties égales que le polygone doit avoir de cotés. Les divisions de la circonférence sont les sommets des angles du polygone; il suffit de joindre par des lignes droites les divisions consécutives.

VOIR cas par cas :

1 Carré :

INFO PLUS ! ! ! !

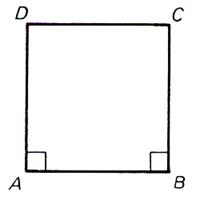
a) Si on connaît le côté AB , tracer en A et B les perpendiculaires à AB et porter AD = AB = BC

b) Si on dessine d’abord une circonférence , tracer deux droites « diamètres » perpendiculaires .

2 - Triangle équilatéral :

INFO PLUS ! ! ! ! !

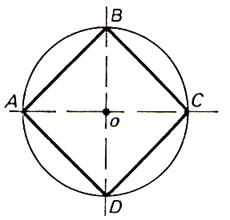
Si on connaît le côté AB , tracer les cercles des centres A et B et de rayon AB .

Si on trace d’abord une circonférence , porter 6 cordes consécutives égales au rayon du cercle et joindre les points comme l’indique la figure .

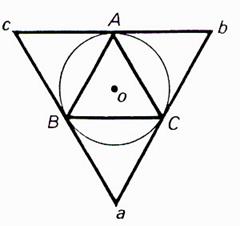
3 ) Hexagone régulier

INFO PLUS ! ! ! !

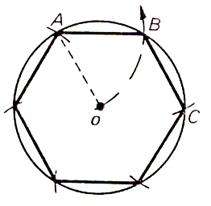
a) Si on connaît le coté AB tracer les cercles de centres A et B et de rayon AB , puis le cercle de rayon OA et de centre O . Tracer à partir de A , 6 cordes consécutives égales à AB

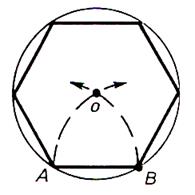
b) Si on dessine d’abord une circonférence, porter 6 cordes consécutives égales au rayon du cercle.

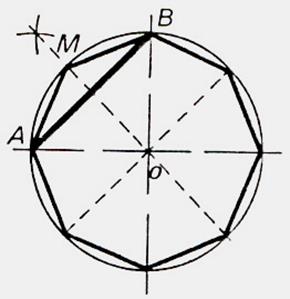
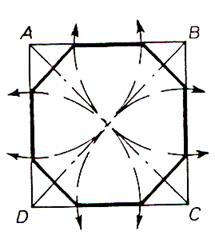
Remarque importante : possibilités de tracés à partir d’un carré

En traçant l’axe de symétrie d’un côté ( exemple AB) du carré , on partage l’arc AB en deux parties égales. En portant des cordes successives égales à MA ou MB , on forme un polygone régulier de 8 côtés ( octogone) . En faisant une construction analogue sur ce nouveau polygone , on tracerait un polygone régulier de 16 côtés .

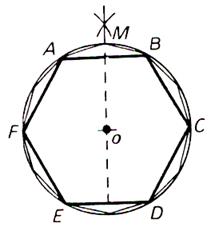
Autre méthode : Une autre construction possible : faire à partir de l’hexagone régulier permet de tracer un polygone régulier de 12 côtés ( dodécagone), puis de 24 côtés .

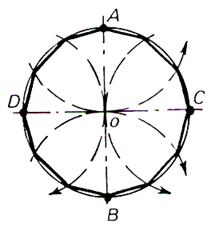
Troisième possibilité. A partir d’un carré de centre O. Le carré A BCD , tracer les diagonales puis les cercles de centres A ; B ; C ; D et de rayons AO ; BO ; CO ; DO

4°) Dodécagone régulier (12 côtés)	INFO PLUS ! ! ! !
Tracer deux diamètres perpendiculaires AB et CD . De A ; B ; C , C décrire des arcs de cercles de rayon AO ; BO ; CO ; DO .

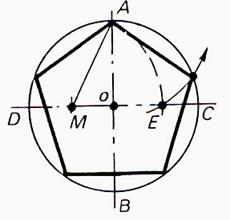
5°) Pentagone régulier: ( 5 côtés)	INFO PLUS ! ! !
Tracer deux droites perpendiculaires , de diamètre AB et CD . Déterminer M milieu de OD . Décrire le cercle de centre M et de rayon MA et déterminer E . Porter ensuite 5 cordes successives égales à AE à partir de A .

6°) Décagone régulier ( 10 côtés)	INFO PLUS ! ! !
Sur la figure précédente , porter à partir de A , 10 cordes successives égales à OE ( voir OE ci dessus)

Remarque importante.

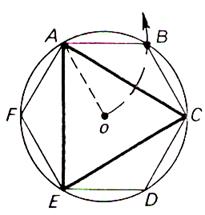
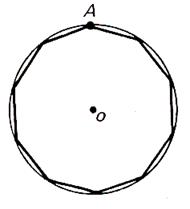
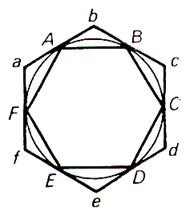
Un polygone régulier est inscrit dans un cercle. Si l’on trace par chaque sommet d’un polygone régulier la tangente au cercle , on construit un polygone régulier ayant la même nombre de côtés.
Exemple 1

	Un polygone régulier est inscrit dans un cercle. Si l’on trace par chaque sommet d’un polygone régulier la tangente au cercle , on construit un polygone régulier ayant la même nombre de côtés.
	Exemple 2 : Voir :INFO PLUS : le milieu
Ici : SUITE du cours sur les tracés		1°) Les polygones étoilés et des tracés de ROSACES

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1. Qu’est qu’un polygone ?

2. Qu’est qu’un polygone régulier ?

3. Citer des polygones réguliers ( 6 ) ?

EVALUATION

Série 1

Nommer les polygones de 5 cotés ou plus

5 cotés

6 cotés

7 cotés

8 cotés

9 cotés

10 cotés

Série 2

Combien de côtés ont les polygones suivants

Le décagone

L’hexagone

L’octogone

L’ heptagone

Le pentagone

L’ennéagone

INTERDISCIPLINARITE