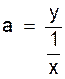Pré requis:

L’inverse d’un nombre
Les segments : représentation
Les intervalles
Les ensembles  R  et  R * : R*
Identification des symboles : :   permettant de traduire       ]  -  ¥  , 0  [ È  ] 0  , + ¥  [

ENVIRONNEMENT du dossier:

Index   warmaths	Objectif précédent   les partages inversement proportionnels	Objectif suivant La fonction homographique	Les grandeurs proportionnelles et inversement proportionnelles

DOSSIER : La grandeur inversement proportionnelle. y =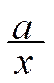

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

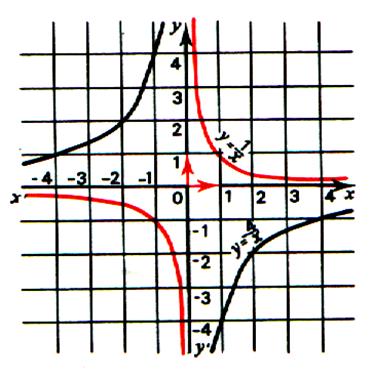
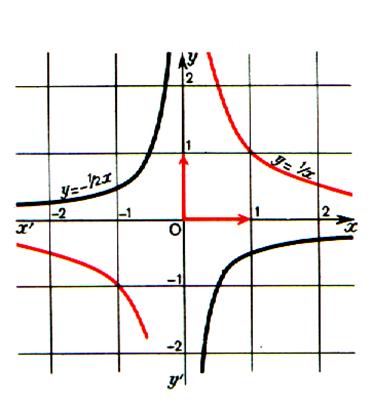
Voir la fonction homographique

 

COURS

 

Les grandeurs inversement proportionnelles 

 

Exemples de situations utilisant les grandeurs inversement proportionnelles :

 

Vie quotidienne :

      Une personne organise une tombola ( grille) et veut mettre en vente des grilles  , à 100 € la grille .Elle hésite entre les grilles à 10 ; 20 ; 25  ou 50 grilles . Quel  serait , dans chacun  des cas , le prix d’une case ?

      Avec une somme d’argent on peut acheter 60 publications coûtant 4,50 € , combien pourrait – on en acheter  si la publication valait 5,40 € ?

 

 

En cinématique :

 

-        Le temps mis par un mobile animé d’un mouvement uniforme et parcourant une distance donné est inversement proportionnel à la vitesse du mobile .  ( relation :      v t = e  )

 En Physique :

 

Le volume « v » d’une masse gazeuse , à une température donnée , est inversement proportionnel à la pression « p » ( loi de Mariotte) : « p v = constante » . Dans tous les cas , si on désigne par « x » et « « y »  les valeurs correspondantes de deux grandeurs inversement proportionnelles , « a » étant constant » , on a les relations suivantes ( égalités) :

 

Ou	Ou	Ou    ( SOS calcul)
x y  = a	y =

 

Définition :  Deux grandeurs  sont  inversement proportionnelles si le produit de deux valeurs correspondantes de ces grandeurs est un nombre constant .

 

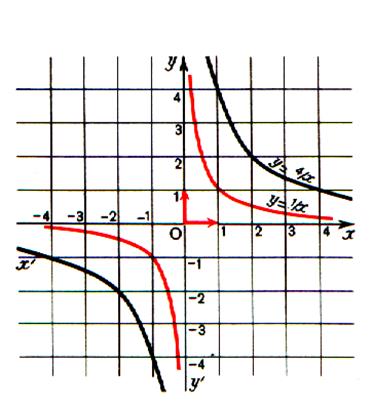
II )   Etude la fonction f    telle que f(x)   =

 

Définition : reprenons le problème Une personne organise une tombola ( grille) et veut mettre en vente des grilles  , à 100 €  la grille .Elle hésite entre les grilles à 10 ; 20 ; 25 ; 50 ; 100  grilles . Quel  serait , dans chacun  des cas , le prix d’une case ?

 

 

Nombres « x » de grilles	Prix « y » d’un case ( en Francs)
10	=  10
20	=  5
25	= 4
50	=  2
100	= 1

 

Ainsi , au  nombre réel « x »  , nous faisons correspondre le réel  appelé « y »   ;  soit  y =

 

Nous pouvons écrire aussi que  y =  100      (   SOS calcul )

 

Ce qui montre que , le prix d’une grille est constante , le prix du billet est proportionnel à l’inverse du nombre de cases . On dit que le  prix d’une case est inversement proportionnel au nombre de cases.

 

Ainsi  si « a » est le prix d’une grille ; « x »  le nombre de cases ; « y » est le prix d’une case ;

Nous avons la relation :        y =  a

 

Remarque : si « a » égal 1 ; la relation s’écrit   y =  1    ; soit  y =

Ecriture  (convention):

 

Puisque la valeur  de « y » variera en fonction de la valeur de « x » ; on remplace « y » par «  f(x) ; ce qui nous  permet de remplacer l’équation y =   par

                                       f(x) =

 

ETUDE de la FONCTION f tel que    f(x) =

Domaine de définition :    (D  f)  

       La fonction  f    tel que    f(x) =   n’est pas définie pour  x = 0    SOS : info plus

  Donc  Le domaine de définition de la fonction  ( noté : D  f    )   x a 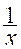      se note : D  f =    R*     

 

                   ou encore     il est la réunion   ( noté : È )   des intervalles 

 

D  f =      ]  -  ¥  , 0  [ È  ] 0  , + ¥  [

 

 

On peut aussi dire : que l’ensemble de définition de la fonction est donc l’ensemble des réels ( R ) privé de l’élément zéro . Cet ensemble se note  R*

 

Extrait d’un tableau de variation numérique :

Nous donnons a « x » des valeurs négatives et positives constamment croissante . On obtient par exemple : ( d’autres valeurs auraient pu être prises)

x	- 10	-5	-1	-1/2	-1/10	« 0 »	+1/10	+1/2	+1	+5	+10
	- =-0,1	- =-0,2	- =-1	-=-2	-=-10	impossible-	+= =  +10	+=   = +2	+ =+1	+ =+0,2	+ =+0,1

 

Constat :

1°) Faisons  pour chaque colonne  les produits : x y    ; résultat xy = 1 

    Le produit x y  est positif ; Donc « x » et « y » sont de même signe .

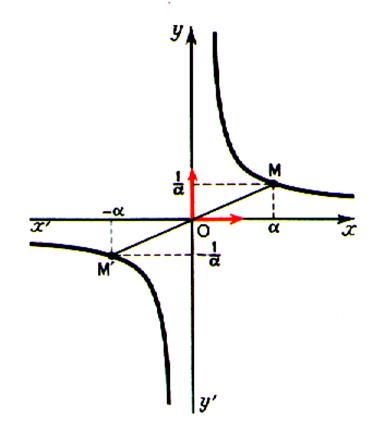
2°)  A deux valeurs de x  (   - 10   et + 10 )  correspondent deux valeurs opposés de y  ( -0,1 et +0,1 ) ; autrement dit   f (-a) = - f(a)  . On dit que la fonction est impaire .

3 °)  On constate que pour des valeurs « absolues » croissantes et de même signe  de « x » , les valeurs de « y » sont décroissantes .

 

 

 

 

 

 

 

 

 

 

 

 

VARIATION de la fonction :

 

a) Considérons deux valeurs quelconques distinctes x₁   et x₂   de même signe auxquelles correspondent respectivement les valeurs  y₁  =     et    y₂   =    on a  

                            (1)      y₂   -    y₁    =    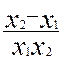  -     =  -        ( SOS calcul)

                        

                 on sait par ailleurs que  (2)    =

 

 

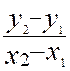
on place   (1) dans (2) :   ( SOS @  calcul)    :    on obtient :   = - 

 

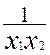
le produit   x₁x₂ étant positif , le taux d’accroissement   est négatif . Donc :

           la fonction  f tel que f(x) =   est décroissante dans chacun des intervalles où elle est définie .

b )  si  ôxô  devient infiniment grand ,    devient aussi voisin de zéro que l’on veut :

pour avoir   <    , il suffit de prendre ôxô  > 10⁶. De même , si ôxô   prend des valeurs de plus en plus  voisines de  zéro    augmente indéfiniment. Pour avoir > 10⁹  , il suffit de prendre ôxô   <  ;

Ainsi : lorsqu’un nombre tend vers ±¥  , son inverse  tend vers zéro . Lorsqu’un nombre de signe donné tend vers zéro , son inverse tend vers l’infini avec le même signe :  ( travail à faire avec la calculatrice )

 

 

 Il en résulte le tableau de variation suivant :

 

 

x	-¥                                0                                     +¥
f(x)= =	0 -                                    +¥                                                                      -¥                                         0 -

 

 

 

Le double trait vertical indique que , pour x = 0 , la fonction n’est pas définie.

 

 

REPRESENTATION GRAPHIQUE DE LA FONCTION :

a) Dans le plan rapporté au repère cartésien ( O , ,  ) nous construisons certains points dont les coordonnées figures dans le tableau :

 

	A	B	C	D	E		G	H	M	N
x	- 3	-2	-1	-1/2	-1/10	« 0 »	+1/10	+1/2	=+2,8	+3
	=-0,33	=-0,5	=-1	-=-2	-=-10	impossible-	+= =  +10	= +2	=+0,357	=+0,333

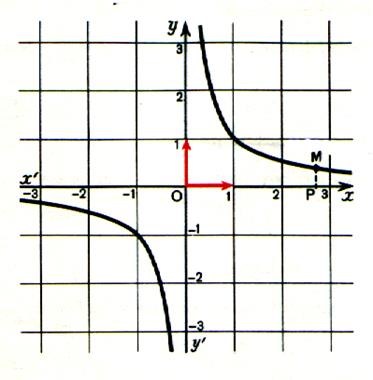
On obtient deux branches de courbe situées dans les quadrants I et III.

 

La courbe d’équation  y =    se nomme  Hyperbole

 

 

 

 

 

 

 

 

TRAVAUX AUTO FORMATIFS.

 

 

CONTROLE:

 

Quelle est la condition  pour que deux grandeurs soient inversement proportionnelles ?

Deux grandeurs  sont  inversement proportionnelles si le produit de deux valeurs correspondantes de ces grandeurs est un nombre constant

Donner les trois égalités permettant d’identifier   une fonction inversement proportionnelle ?

 

 

y =

a =

 

.

 

 

 

 

 

EVALUATION: