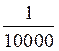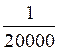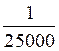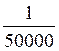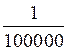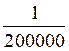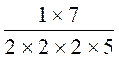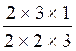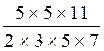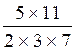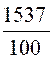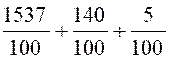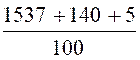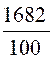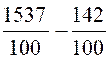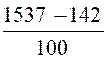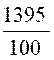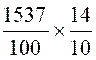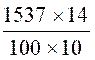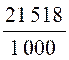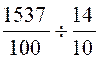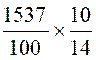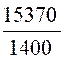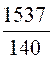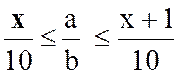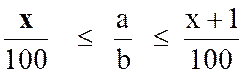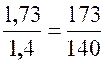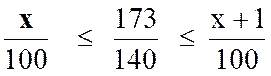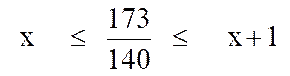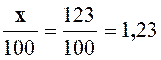Pré requis:
|
|
|
|
Le
nombre décimal (nomenclature) |
|
|
La
fraction "irréductible" |
|
|
Relation
entre D et un N divisé par 10 ou un multiple de dix |
|
|
Nombre
décimale et fraction |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Objectif
précédent : |
Objectif
suivant : |
92 DOSSIER : La fraction représentante d ' un
nombre décimal
|
COURS |
Interdisciplinarité |
|
|||||
|
|
|
|
|
|
|
|
Objectif :
Rechercher si la fraction est le représentant d’un nombre décimal
Définition de l’objectif :
Savoir dire si une fraction ou une écriture fractionnaire est la représentante
d’un nombre décimal.
Rappel: on
appelle "nombre décimal "
le quotient d’un nombre entier (rationnel) par 10 ou une puissance de 10.
Condition: pour savoir si une fraction est la représentante d’un nombre
décimal il faut tout d’abord décomposer le numérateur et le dénominateur en
produit de facteurs premiers ,lorsque la fraction est rendue irréductible ,on
pourra ensuite analyser le produit de facteurs se trouvant au dénominateur.
|
Règle: Une fraction est la représentante d’un nombre décimal si
la fraction
irréductible équivalente ,ne possède au
dénominateur pas d’autres facteurs premiers que des 2 ; des 5 ;des 2 et des 5. |
Procédure: pour savoir si une fraction est la représentante d’un nombre décimal il
faut:
1°) Décomposer le numérateur est le dénominateur en
produit de facteurs premiers
2°) Rendre irréductible la fraction en
supprimant les facteurs communs de même indice.
3°)Analyser
les facteurs premiers du dénominateur
pour conclure:
Si il y a un facteur premier autre que 2 et 5 ,on
conclut que la fraction n’est pas la représentante d’un nombre décimal.
Si il n’y a que des 2 ,ou des 5 ou des 2 et de
5 ,on conclut que la fraction est la représentante d’un nombre décimal.
On peut trouver en divisant avec une calculatrice la valeur
décimale d’une fraction :
|
Exemples utilisés dans les calculs d’échelle : Les fractions ci dessous ont
pour |
« nombre
décimal » : |
|
0,0002 |
|
|
|
0,0001 |
|
|
0,00005 |
|
|
0,00004 |
|
|
0,00002 |
|
|
0,00001 |
|
|
0,000005 |
Exercices types:
Question: Est ce que les fractions suivantes représente
des nombres décimaux?
7 / 40 ; 3 / 25 ; 6 /12 ; 275 /210
Réponses:
=
= .............
La fraction est irréductible ,le dénominateur ne contient que des facteurs
premiers « 2 » et
« 5 » ,on peut alors conclure
que la fraction « 7/40 »
représente un nombre décimal ; ce nombre , après calcul est 0,175
(soit la fraction 175/1000 )
à Voir : comment on a obtenu =
(fractions
équivalentes)
=
=
.................... La fraction est irréductible , le dénominateur ne contient que des facteurs
premiers 5 ,on peut alors conclure que
la fraction 3 / 25 représente un nombre décimal ; ce nombre , après calcul
est 0,12 (
soit 12/100)
= 
= (on doit rendre irréductible)=
=...............
La fraction est irréductible ,le dénominateur ne contient que des facteurs
premiers 2 ,on peut alors conclure que la fraction « 6/12 » représente un nombre décimal ;
Ce nombre décimal , après
calcul, est 0.5
(soit 5 /10)
=
= on rend
irréductible = 
=........
la fraction est irréductible ,le dénominateur contient autres
facteurs premiers que des 2 et ou 5 ,on conclut que la fraction
« 275/210 » n’est pas
représentante d’un nombre décimal.
(Si nous posons et faisons la division nous constatons
que nous n’arrivons pas à avoir la valeur exacte du quotient)
TRAVAUX
AUTO FORMATIFS.
Comment procède - t
- on pour savoir si une fraction est la représentante d’un nombre décimal ?
I) trouver
le nombre décimal représentant les fractions suivantes :
|
|
Forme décimale : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I ) Les fractions suivantes
sont-elles des représentantes d’un nombre décimal ? (dites pourquoi et éventuellement donnez la valeur exacte du
quotient .)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
105/35 |
|
|
|
7/56 |
|
|
|
10/33 |
|
|
|
21/135 |
|
|
|
5/27 |
|
|
II ) faire la même chose mais avec des nombres relatifs.