Définition de l ‘ objectif : Savoir construire une fraction
égale à une fraction donnée.
Pré requis:
|
Info : Sommaire |
|
|
Sciences : fractions égales (longueurs) |
|
ENVIRONNEMENT du dossier :
|
1°)
fraction égale ( primaire) notions : Travaux :
dossier 120 : partage en part égales |
2°) >> La
proportionnalité |
LES FRACTIONS « EQUIVALENTES » et « NON
EQUIVALENTES »
dit aussi : les fractions égales et inégales .
1°) Les fractions équivalentes (
égales)
2°) Comparaison et classement entre deux fractions inégales.
·
A ) Comparaison de deux fractions .
·
B
)
Comment classer ou ordonner des
fractions par ordre croissant ou décroissant?
·
C ) Comparaison d’une fraction à l’unité.
|
COURS |
Interdisciplinarité |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
COURS
1°) LA FRACTION EQUIVALENTE *(à une autre fraction):
-*Cette
notion est trés importante; elle est la clef du
travail sur les proportionnalités.
n
Equivalente : veut dire « de même valeur »;
n
donc on
dira que : deux
fractions dites « équivalentes » sont des fractions qui représentent
la même valeur.(racine latine :« équi » qui signifie « égal »)
-Remarque.
Des fractions (ou écritures
fractionnaires)peuvent représenter un même nombre:
exemple:
la division 48 / 12 = 4
20 / 5 = 4
4.8 / 1.2 = 4
4 / 1 = 4
on peut donc écrire que 
= 
= 
= 
= 4
Deux fractions séparées par le signe « égal » sont dites
« fractions équivalentes »
Modèle mathématique:
=
(b et d
sont différents de 0)
Question : SONT
- ELLES « EQUIVALENTES » ;on "pourrait" dire
" égales" ? ? ? ? ?
Première
méthode :
Les deux
fractions 
et 
sont
égales si ……
si la division de et la
division de donne le même rationnel
.
Exemple:
Exemple numérique:
Question : est ce que les deux fractions suivantes sont
"égales" ?
Réponse:
oui si la division 48:12 est égale à
20:5
Calcul :
|
48:12 = 4 |
|
|
20:5
= 4 |
|
Conclusion
: le quotient étant "exact" ;les deux
fractions sont égales , on dira
"équivalentes"
Deuxième
méthode:
Pour vérifier si deux
fractions ( et ) sont
équivalentes il faut multiplier le
numérateur de l'une avec le dénominateur de l'autre ,les deux produits ( ad et cb )
doivent être égaux.
et sont égales si
……
Réponse : OUI
, si ... « le produit......."ad "est
égal au produit "cb" »
Exemple : dire si les deux fractions 
et 
sont
équivalentes
Résolution:
On écrit :
et sont égales si
…8 fois 33 = 11 fois 24
On calcule :
8 fois 33 =
264 ; 11 fois 24
= 264
On conclut :
les produits sont égaux , les fractions et sont
équivalentes
Des fractions qui ne sont pas
équivalentes peuvent être « comparées » et « classées » par ordre de
grandeurs !
2°) LES FRACTIONS INEGALES. (info +++ Notion sur la
comparaison)
A ) Comparaison de deux fractions .
Cas 1 :
les fractions ont le même dénominateur :
Si
deux fractions ont le même dénominateur , la plus
grande est celle qui a le plus grand numérateur .
|
Soient les fractions Donc |
|
Cas 2 : les
fractions ont le même numérateur , mais elle
ont un dénominateur différent :
Si deux
fractions ont le même numérateur , la plus grande est
celle qui à le plus petit dénominateur.
Lorsque les fractions ont pour numérateur 1 , l’affirmation est évidente .
Ainsi 
pain est plus grand qu’un 
de pain .
|
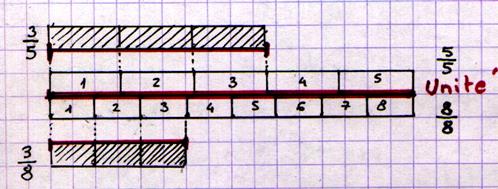
Soient les fractions En effet , ces fractions
représentent chacune 3 parties de l’unité ; mais les parties de la
première , étant des cinquièmes , sont plus grandes que celles de la seconde
, qui sont des huitièmes . Donc |
|
|
Autre
exemple : Soit à comparer |
|
|
B
)
Comment classer ou ordonner des fractions par ordre croissant ou
décroissant?
Trois façons possibles :
1°) en
effectuant un calcul « approché » :
Pour ordonner des fractions il suffit :
a )de rechercher pour chacune d'elle la valeur du rationnel
afin d'obtenir une forme décimale (faire la division),
b) classer
les valeurs décimales ,
c ) pour remplacer ensuite ces valeurs par les fractions
données.
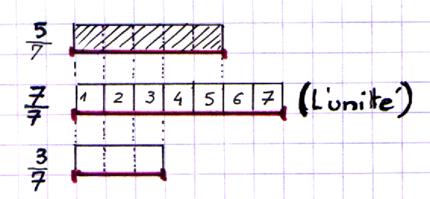
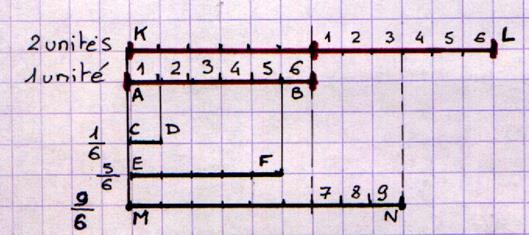
2°) Graphiquement . (voir les travaux
précédents sur les longueurs des segments de droite)
3°) voir
aussi leçon sur le produit en croix :
|
SOS info :
Produit en croix |
C ) Comparaison d’une fraction à l’unité.
|
1°) Une fraction est
inférieur à l’unité si son numérateur est plus petit que son dénominateur .
2°) Une fraction est
égale à l’unité , si son numérateur est égal à son dénominateur .
3°) Une fraction est
supérieure à l’unité si son numérateur est plus grand que son dénominateur.
|
|
D ) Expression
fractionnaire :
une fraction égale ou supérieure à l’unité est encore
appelée expression fractionnaire.
Travaux auto formatifs
2 ° ) Par quel signe
sont séparées deux fractions équivalentes?
3° ) Que représente deux fractions équivalentes , autre qu
‘une égalité ?
4 ° ) Donnez le modèle mathématique représentant deux
fractions équivalentes.
5° ) Comment peut-on procéder pour ordonner ( classer dans un ordre croissant ou
décroissant ) des fractions ?
6° ) Comment procède -t - on pour vérifier si deux fractions
sont équivalentes (donnez la procédure la plus sûre ) ?
I )Dire si les fractions suivantes
sont équivalentes (si non les classer par ordre croissant):
a ) 
; 
; 
; 
;
; utiliser le
tableau ci dessous ;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b )idem que ci dessus : 
;
;
;
;
c ) idem que ci dessus :
;
; 
II
)
Construire .....5......fractions équivalentes à la fraction donnée : 
III) On nous donne deux
fractions ;
et 
;sont-elles équivalentes?
En complément :voir cas avec nombres relatifs
I ° ) Construire 3 fractions équivalentes à la
fraction donnée.(indiquer le coefficient multiplicateur utilisé pour chaque
étape)
*un « coefficient » est un nombre
,généralement , entier .
a) 
=
b) 
=
c) 
=
d)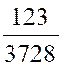 
=
II ° )
CALCUL ALGEBRIQUE :
Mettre sous forme d’une
égalité simple les fractions équivalentes suivantes ,en utilisant le produit en
croix :
|
|
|
|
|
|
|
|
|
et encore :
a) 
= 5
b) 
=
7 ;
Construire 4 fractions équivalentes à la fraction à la
donnée
a) 
=
b)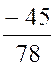 
=
c) 
=
d) 
=
Dans
les exercices suivants ne pas « développer »
e)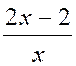 
=
f)
=
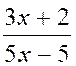CORRIGE
EVALUATION
I ) a) ligne 2 : calcul
avec la calculatrice
ligne 3 : classement par ordre croissant.
|
|
|
|
|
|
|
0,28333 |
0,250 |
0,8337 |
0,583 |
0,600 |
|
2 |
1 |
5 |
3 |
4 |
|
|
|
|
|
|
conclusion : 
<
< 7/ 12
< 
<
Voir «
les proportions »