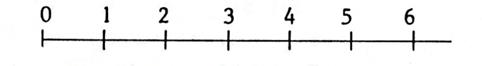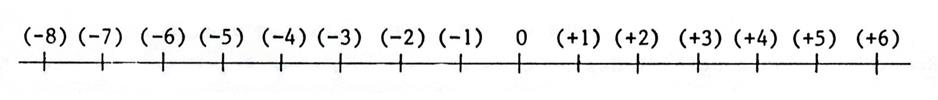|
|
|
|
|
|
|
DOSSIER :
LES DECIMAUX RELATIFS Lici liste des
cours consacrés aux nombres décimaux |
Vers le corrigé… |
ENVIRONNEMENT du dossier:
DOSSIER : Nombres
relatifs : ADDITION et
soustraction de « RELATIFS »
|
|
Fiche
1 : Les nombres relatifs : le nombre entier relatif, le décimal relatif,
simplification, droite graduée…. |
|
|
|
Fiche
2 : Addition de deux nombres relatifs. |
|
|
|
Fiche
3 : Propriétés de l’addition des nombres relatifs. |
|
|
|
Fiche
4 : Somme
de plusieurs nombres relatifs. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
Cette leçon est très très importante , elle est une des bases fondamentales… |
|
|||||||||||||
|
|
Le nombre relatif n’est pas qu’un
« simple nombre », il ne devrait pas avoir de forme
simplifiée !!!! C’est
un nombre dit « nombre algébrique » ; |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Fiche
1 : Les nombres relatifs. |
Sos :info
2 Complément sur ce qu’il faut savoir
sur les nombres relatifs |
|
||||||||||||
|
|
A ) Les entiers relatifs : En classe
de 6ème , vous avez rencontré des entiers
relatifs . Exemples : ·
( -9) ; ( ( + 11
) ; ( 0 ) ; ( - 67 ) ; ( + 7 ) ; ( + 863) sont des nombres entiers relatifs. ·
( + 7 ) ; ( + 693) ; ( + 73 ) : sont des entiers relatifs positifs . Leur
signe est : ..+
…. ·
( - 7 ) ; ( - 693 ) ; ( - 73 ) : sont des entiers relatifs
négatifs . Leur signe est : ..- …. ·
« 0 » ( zéro) est à la fois « positif » et
« négatifs ». |
|
|||||||||||||
|
|
B ) L’opposé d’un nombre
relatif. |
|
|
||||||||||||
|
|
§
( - 8 ) et ( + 8 ) sont des entiers relatifs « opposés »
. |
SOS : cours sur
« opposé » d’un nombre |
|
||||||||||||
|
|
On écrit ( - 8 ) = Opp. ( + 8 ) |
Lire :
« ( - 8 ) est égal à l’opposé de ( + 8
) » |
|
||||||||||||
|
On écrit ( + 8 ) = Opp. ( - 8 ) |
Lire :
« ( + 8 ) est égal à l’opposé de ( - 8
) » |
||||||||||||||
|
|
Activité n°…. |
|
|||||||||||||
|
|
Complétez : |
|
|
|
|
|
|
||||||||
|
|
Opp. ( - 23 ) = |
……( + 23)…. |
Opp. ( + 57 ) = |
…( - 57 ).. |
Opp. ( 0 ) = |
……( 0 )…… |
|
||||||||
|
|
|
|
|||||||||||||
|
|
C) Simplification d’ l’écriture d’un entier
relatif. |
|
|
||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||
|
|
Ci-contre
la représentation
graphique des nombres entiers naturels..→ |
|
|
||||||||||||
|
|
Ci- dessous
représentation des entiers relatifs. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Vous
voyez que les entiers positifs occupent la même place que les entiers
naturels. §
C’est la raison pour
laquelle on les confondra et on écrira par exemple … ( +
7 ) =
7 ( warmaths vous met en garde contre cette simplification…..) §
Dans le cas de
« négatif » , si le nombre est seul, on
peut ne pas mettre les parenthèses . Par exemple : on écrira « - 5 » à la place de « ( - 5) ». ( warmaths vous met en garde contre
cette simplification…..) |
|
|||||||||||||
|
|
D : Les décimaux relatifs. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Voici des
décimaux relatifs ( - 13 , 9 ) ; ( + 43 , 86 ) ; ( - 0, 0 5 ) ;….. comme pour les entiers, on peut simplifier
l’écriture : - 13,9 ; 43,86 ; 0,05 |
|
|||||||||||||
|
|
§
Tout nombre entier
peut être considéré comme un nombre décimal. Par
exemple « 73 » peut s’écrire « 73,00 ». De même ( + 47 ) peut s’écrire
( 47 , 000) ou 47,
000 : Et même : ( - 5 ) peut s’écrire ( 5 , 0 ) ou
- 5,0 Donc tout
entier relatif peut être considéré comme un : nombre
décimal… Par la suite , on dira souvent « nombre relatif » sans
distinguer entier ou décimal. ·
( - 8 , 57 ) et ( + 8 , 57)
sont deux décimaux relatifs …………………opposés…. |
|
|||||||||||||
|
|
Activités n°…. |
|
|
|
|
||||||||||
|
|
Opp. ( + 0 , 007 ) =
………… |
( - 0 , 007) |
Opp. ( - 53, 29 ) = ………. |
( + 53 , 29 ) |
|
||||||||||
|
|
Tout nombre
relatif possède un opposé unique. Comment l’ obtient-on ?..........................................Il suffit de prendre le nombre relatif est changer le signe + en - ou
- en plus…. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
E : Droite graduée (
simplifiée !!! attention danger )…. |
|
|
||||||||||||
|
|
Sur la
droite ci-dessous ,nous avons placé des
points……..identifiés par des lettres…….. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
On
dit que : |
|
|||||||||||||
|
|
|
Forme
simplifiée |
Forme « normalisée » |
|
Forme
simplifiée |
Forme « normalisée » |
|
||||||||
|
|
Le point
« A » a pour abscisse : |
4 |
( + 4 ) |
Le point
« E » a pour abscisse : |
2,3 |
( + 2,3 ) |
|
||||||||
|
Le point
« B » a pour abscisse : |
-
2 |
( - 2 ) |
Le point
« F » a pour abscisse : |
-3,7 |
( - 3,7) |
||||||||||
|
Le point
« C » a pour abscisse : |
1 |
( + 1 ) |
Le point
« G » a pour abscisse : |
-0,8 |
( - 0,8 ) |
||||||||||
|
Le point
« D» a pour abscisse : |
-5 |
( - 5 ) |
Le point
« H » a pour abscisse : |
5,6 |
( + 5,6) |
||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fiche
2 : Addition des nombres relatifs. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
(@revoir les
deux cours traités en 6ème) :@ cours 1 ; @ cours 2 ;. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Lorsque vous aurez revu le cours vous devriez trouver
les valeurs de la somme…. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Opérations
|
On vous
demande de calculer la : |
Situation
problème |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( + 23 ) + ( + 12 ) = ………( + 25 ) |
Somme de
deux nombres de signe « + » |
Vous imaginez
qu’un caissier reçoit 23 € , puis reçoit à nouveau
12 € |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( - 19 ) + ( - 45 ) = …………( - 64 ) |
Somme de
deux nombres de signe « - » |
Vous
imaginez qu’un caissier paie 19 € , puis paie à
nouveau 45 € |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( + 68 ) + ( - 41 ) = ………….( + 27 ) |
Somme de
deux nombres de signe contraire. |
Vous
imaginez qu’un caissier reçoit 68 € , puis paie 41€ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« 68 »
est plus grand que « 41 » ; le signe « + » est le signe
que possède la plus grande valeur numérique…. Le
résultat est un nombre relatif qui a le signe du nombre relatif qui a la
plus grande valeur numérique ;..et qui a pour
valeur numérique la différence entre la plus grande valeur numérique moins la
plus petite valeur numérique…ce qui donne : ( + ( 68 – 41 ) ) = ( + 27) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( - 49 ) + ( + 35 ) = ………( - 14 ) . |
Somme de
deux nombres de signe contraire. |
Vous
imaginez qu’un caissier paie 49 € , puis reçoit 35 € |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« 49 » est plus grand que « 35 » ; le signe « - » est le
signe que possède la plus grande
valeur numérique…. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( + 27 ) + ( - 89 ) = ………( - 62 ) |
Somme de
deux nombres de signe contraire |
Vous imaginez
qu’un caissier reçoit 27 € , puis reçoit à nouveau
89 € |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« 89 » est plus grand que « 27 » ; le signe « - » est le
signe que possède la plus grande
valeur numérique…. :
( - ( 89 – 27 ) ) = ( - 62) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( - 13 ) + ( + 45 ) = ………( + 32 ) |
Somme de
deux nombres de signe contraire |
Vous
imaginez qu’un caissier paie 13 € , puis reçoit 45 € |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« 45
» est plus grand que « 13 » ; le signe « + » est
le signe que possède la plus grande
valeur numérique…. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Dans tous
les cas , pour trouver le résultat ,
vous remplacez chaque nombre
positif par une recette et chaque nombre négatif par une dépense……. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Remarque 1 : on a utilisé
des nombres entiers, mais on peut faire de même avec des décimaux… |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Remarque
2 : porte sur le vocabulaire : La « valeur numérique » d’un nombre relatif porte
le nom de «@ valeur absolue » |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Exemples : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
La valeur absolue de ( +23) est |
« 23 » |
La valeur absolue de ( -
19 ) est |
« 19 » |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Activités
n°… |
Donnez la
valeur absolue des nombres relatifs : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( + 12 ) à
pour valeur absolue : 12 |
( + 68 ) à
pour valeur absolue : 68 |
( + 35 ) à
pour valeur absolue :…. |
( -13 ) à
pour valeur absolue :…. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( - 19 ) à
pour valeur absolue : 19 |
( - 41 ) à
pour valeur absolue : 41 |
( + 27 ) à
pour valeur absolue :…… |
( + 45) à
pour valeur absolue :….. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( - 45 ) à pour valeur absolue : 45 |
( - 49 ) à
pour valeur absolue : 49 |
( - 89 ) à
pour valeur absolue :….. |
( + 12, 6 ) à pour valeur absolue :…. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Avant
d’énoncer @ la règle de l’addition
des nombres relatifs , vous pouvez retenir le schéma
suivant. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A) Les nombres ont le
même signe : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
On
calcule la somme des valeurs absolues |
Résultat |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( + 3 ) + ( +
5 ) |
Le signe de la somme est « + » |
3 + 5 = 8 |
( + 3 ) + ( + 5 )= ( + 8 ) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( - 3 ) + ( -
5 ) |
Le signe de la somme est « - » |
3 + 5 = 8 |
( - 3 ) + ( - 5 )= ( - 8 ) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
B ) Les nombres sont de
signe différent (contraire). |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
( + 3 ) + ( - 5 )= …….. |
5
> 3 ; le signe de la somme
est celui de ( -
5 ) , le signe - (moins) ; d’où le calcul : 5 – 3 = 2 |
( + 3 ) + ( - 5 )= ( - 2 ) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( - 4 ) + ( + 9 )= …….. |
4 <
9 ; le signe de la somme est celui de ( +9 ) , le signe + (plus) ; d’où le calcul : 9 – 4 = 5 |
( - 4 ) + ( + 9 )= ( + 5 ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
On retiendra : sur l’addition de deux
nombres relatifs : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1°) La somme de deux nombres de même signe est égale à un
troisième nombre relatif qui aura -
pour signe :
le signe commun -
pour valeur absolue : la somme des deux
valeurs absolues 2°) La somme de deux nombres relatifs de « signe différent
» ;(
un nombre de signe + l’autre de signe -
et inversement l’un de signe -
l’autre de signe +) est égale à un
troisième nombre relatif qui aura : -
Pour « signe » : le signe du nombre relatif qui à la plus grande valeur absolue. - Pour valeur absolue: La différence (soustraction *) des valeurs absolues; toujours la plus grande valeur absolue moins la plus petite
valeur absolue. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activités n°…. Effectuez les opérations suivantes .avec des
entiers relatifs. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
( + 28 ) + ( - 13 ) = ……… |
( + 15 ) |
( + 6 ) + ( + 23 ) = ………. |
( + 29 ) |
( + 11 ) + ( - 11 ) = …………. |
0 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( - 24 ) + ( + 58 ) =………. |
( + 34 ) |
( + 5 ) + ( - 17 ) = ………. |
( - 12 ) |
( - 29 ) + ( 0 ) = ……… |
( - 29 ) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( - 51 ) + ( - 36 ) = ……… |
( - 87 ) |
( 0 ) + ( + 19 ) = ……… |
( + 19 ) |
( - 37 ) + ( + 28 ) = ……… |
( - 9 ) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Effectuez les opérations suivantes .avec des
décimaux relatifs. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( + 18,37 ) + ( - 54,07 ) =
……… |
( - 35 , 70) |
( - 53 ,80 )
+ ( + 41,253 ) = ……… |
( - 12,547) |
( - 0,09 ) + ( - 0,038 ) = ……… |
( - 0,128) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vocabulaire :
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
( + 7 ) + ( - 5 ) = ( + 3) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
- ( + 3
) est la …somme….. de ( +
7 ) et de ( - 5) - ( + 7 ) et (
- 5) sont les ….termes … de la même somme. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
L’opération
correspondante s’appelle : …….l’addition… |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Info @ 1……. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fiche
3 : Propriétés de l’addition des nombres relatifs. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A ) la commutativité . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Calculez : ( + 3 ) + ( - 7 ) = ……( - 4 )……. Et ( - 7 ) + ( + 3
) = ……(- 4)…. Vous
pouvez donc écrire : ( + 3 ) + ( - 7 )
= ( - 7 ) + ( + 3 ) Vous
pouvez choisir d’autres nombres , vous constaterez
toujours que la somme ne change pas si
l’on permute les termes .On dira alors : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A retenir : « L’addition
des nombres relatifs est
commutative » ,
cela signifie : Pour tous
nombres relatifs « a » et
« b » , « a +
b = ….. b + a ……….»
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
B)
L’associativité. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité :
………..Complétez : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
( - 7 ) + |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= (
- 3
) + ( - 6 )
= (
- 9 ) |
|
= ( - 7 )
+ ( - 2
) = (
- 9 ) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vous pouvez donc écrire : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vous
pouvez choisir d’autres nombres , vous constatez toujours
que la somme ne change pas si l’on place différemment les parenthèses dans
cette somme, on dira alors : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A retenir : « l’addition
des nombres relatifs est associative » , cela signifie : Pour tous nombres relatifs « a » , « b » et
« c » , « ( a + b ) + c =
….. a +
( b + c) ……….» |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Puisque
la place des parenthèses n’importe pas , on convient
d’écrire la forme simplifiée « a
+ b + c » à la place de «
(a + b ) + c » ou «
a + ( b + c ) » |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
C ) L’élément neutre. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Calculez |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
( - 19 ) +
0 =…………. |
( - 19 ) |
0 + ( + 27 ) = ……. |
( + 27 ) |
( - 33, 49 )
+ 0 = ……… |
( - 33, 49 ) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A retenir « 0 »
est l’élément neutre pour
l’addition des nombres relatifs . Cela
signifie que : Pour tout
nombre relatif « a » , « a + 0 = …a.. » ;
« 0 + a = …a.. » |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
D
) L’opposé … « unique ».. |
SOS.
@Propriété utiliser pour transformer une égalité ou « résoudre une
équation ».. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vous
savez que « ( +
7 ) » et « ( - 7 ) »
sont deux nombres relatifs …………………….opposés….. On
écrit : Opp ( + 7 ) = ………………( - 7 ) …… et Opp ( - 7 ) = ……………( + 7 )…. ( + 7 ) + ( - 7 ) = ……………0……………..donc ( + 7 ) +
Opp ( +7) = …0………. De
même : (
- 13,5 ) + Opp ( - 13 , 5 ) =
……………0……. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A retenir : Tout nombre relatif possède un opposé unique. Pour tout nombre relatif « a » , « a +
Opp ( a ) = …0…. » |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
·
Inversement
, on peut prouver que si la somme de deux nombres
relatifs est nulle, alors ces deux nombres sont opposés l’un de l’autre. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A retenir : Si « a + b = 0 » alors
« a = Opp ( b ) »
et « b = Opp ( a ) » |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité :
n°….. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Calculez :
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Opp ( Opp ( - 5 ) ) = Opp …(+5) …..=
…….( - 5 ) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Opp ( Opp
( + 4,9 ) ) = Opp …( - 4,9)……. = ( + 4,9 )……… |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A retenir : Pour tout
nombre relatif « a » , Opp |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité N°……. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Calculez :
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A = |
A = ( + 4 ) + ( - 9 ) + ( +11)= ( - 5 ) +
( +11) |
A = ( +
6 ) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
B = |
B = |
B = ( -
2) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
C = ( - 6 ) + |
C = ( - 6 ) + ( + 2 ) |
C = ( - 4 ) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fiche 4 : Somme de
plusieurs nombres relatifs. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
En
principe, on ne sait pas calculer :
A = ( - 15 ) + ( + 28 ) + ( +37 ) + ( - 67) , on ne sait que traiter que deux nombres à
la fois , ce qui permet de dire que l’écriture de « A » est la forme simplifiée
( par convention) de : Par exemple :
Poursuivez
le calcul . A = ……………………………………..=
………………………..=……………………….. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vous
pouvez imaginer d’autres façons de placer les parenthèses, puis effectuez le
calcul.. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A = …………………………( -15 ) [ ( ( +28 )+
( + 37 ) ) + ( - 67 ) ] Autre façon :
A = …………………………………….. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Dans la
pratique : Etant
donné une somme de plusieurs termes sans parenthèses ,
pour effectuer le calcul , on peut imaginer une succession de parenthèses et
crochets comme dans la première façon.
Ceci revient à dire que l’on additionne le premier le premier terme
avec le deuxième, le résultat obtenu avec le troisième et ainsi de suite
jusqu’au dernier terme. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité
n°… Utilisez
la méthode précédente pour calculer : B = ( +
13 ) + ( - 17 ) + ( - 23 ) + ( + 43 ) + ( - 24 ) + ( + 53 ) = ……….. ……………………………… |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Autre
méthode : Grâce à la commutativité et à l’associativité, on peut
regrouper les nombres positifs d’une part et les nombres négatifs d’autre
part. Appliquez
cette méthode pour calculer « B » .
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Faites de
même pour « C ». C = ( + 27 ) + ( - 53 ) + ( + 18 ) + ( + 45 ) +
( - 12 ) + ( - 23 ) + ( + 14 ) C = ………………………………………………………………………………………………………………….
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Autre
possibilité : Il se
peut que dans la suite de nombres à
additionner figurent des opposés. On peut
alors les regrouper de manière à faire apparaître leur somme qui est : ……..0…….. D = ( - 3 ) + ( + 2 ) + ( + 4 ) + ( + 9 ) + ( +
3 ) + ( - 4 ) + ( - 2 ) D = [ ( + 3 ) + ( - 3 ) ] + [ ( + 2 ) +
( - 2 ) ]
+[ ( + 4 ) + ( - 4 ) ] + ( + 9 ) D = 0 + 0 + 0 + ( + 9 ) D = (
+ 9 ) Dans la
pratique , on se contente de souligner les termes opposés.. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a) Combien y a t il de cas à traiter dans l '
addition des nombres relatifs? 1°) citer la règle concernant
l’addition de deux nombres positifs. (donner le modèle
mathématique)
2) citer la
règle concernant l’addition de deux
nombres de signe négatif. (donner le
modèle mathématique) 3°) citer la règle de
l’addition de deux nombres de même signe. (donner les deux modèles mathématiques) 4°)citer
la règle concernant l’addition de deux nombres de signe contraire. (donner les deux
modèles mathématiques) 5°) Traduire sous forme littérale les quatre égalités
suivantes: 6 ° ) Donner la procédure permettant de faire
les calculs dans une somme algébrique. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
effectuer les opérations suivantes
(donner les étapes) Effectuer les opérations suivantes ,( à transformer ): donner sous forme relative la valeur
de « x et y »: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||