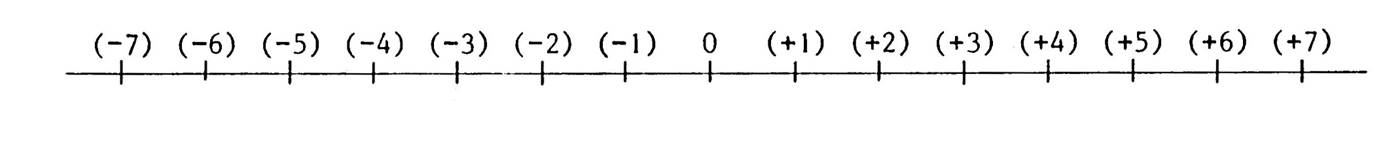DOSSIER : LES DECIMAUX non - relatifs / objectif cours 12

Niveau V  CAP

INFO prof :  Tout exercice sur les nombres relatifs donné sous la forme :  3 – 7 ;ou ;  3 + 7  est faux ; parce que « trois » est la valeur absolue de deux nombres relatifs opposés .   3 n’est pas la forme simplifiée du nombre relatif  +3  ( voir le  cours ) .

Pré requis :

Le nombre décimal
Les nombres positifs ou négatifs ; dits aussi « algébrique »

ENVIRONNEMENT du dossier:

Index

Objectif précédent : Les décimaux relatifs (notions)

Objectif suivant : Le nombre décimal relatif (suite) 1°) les rationnels 2°)Les nombres réels 3°)calcul algébrique :la valeur absolue

Tableau        52 2°) INFORMATIONS  Présentation des opérations avec les décimaux relatifs

 

DOSSIER  Le NOMBRE RELATIF (entier ou décimal)

-        Vocabulaire : les nombres relatifs sont aussi appelés «  nombres algébriques »

-         Attention danger : la simplification d’un nombre positif pose plus de problème qu’il peut en résoudre. ( voir le calcul algébrique et les transformations d’une égalité)

-         l’ Ensemble  «  Z  et  D^{+ ou -} »

-         Représentation graphique des nombres relatifs

ST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

Exemples d’énoncés d’opérations n’entrant pas dans le cadre des opérations avec des nombres relatifs :

12 + 6,5  =	14,5 – 28,3 =	2,3 4,65	( -3,5)  1,5
2,7  ( - 8) =	95 : 4	5,2 : ( + 2,6)	( -3,8) : 4
12 ; 6,5 ; 14,5 ; 2,3 ; 4,65 ; 1,5 ; 2,7 ; 95 ; 4 ; 5,2 ;4 ne sont  pas des décimaux relatifs positifs ! ! ! ! ! !

 

COURS

 

 

 LE NOMBRE RELATIF:

 

Il est composé de  quatre  "symboles ":

 

                  une parenthèse ouverte

 

                                       - un signe  + ou -

                                               

                                                              des chiffres séparés ou non par une virgule

                                                                                           

                                                                                                              une parenthèse  fermée

 

 

Valeur absolue

-

+

         (  _   ______    )                 

 

 

 

 

( + 3)   et    - 3  )   sont des nombres relatifs   ;       Attention !!!!     « 3 »     n’est pas un nombre relatif

 

 

 

 

 

 

 

VOCULAIRE :

 

Ce qu’il faut savoir sur un nombre décimal relatif.

 

 Voir OBJ. 1 (nomenclature)

                  Un nombre décimal relatif est un alignement horizontal de chiffres séparés ou non par une virgule(cet ensemble chiffres et virgule  s’appelle valeur absolue) et  est précédée par un signe  + ou  -.

    Un nombre décimale  relatif  est donc  composé d’ une valeur numérique précédée par un signe ,la valeur numérique et le signe sont , par convention , entourés par une  parenthèse .une   « dite ouverte  » et l’autre « dite fermée. »

 En résumé :  Un nombre relatif  est  composé de deux parties  situées à l’intérieur de parenthèses : la première partie s’appelle « signe » ,l’autre partie « valeur absolue ».

Exemples :   ( + 3,2 ) ; ( - 3,2 )

Valeur absolue : ?

Pour indiquer que 3,2 est la valeur absolue du nombre relatif : nous écrivons

                       ½( - 3,2 ) ½ =    3,2                   ½ ( + 3,2 ) ½ =  3,2

un nombre relatif positif et négatif peuvent avoir la même valeur absolue ! .

ainsi « 3,2 »  est la valeur absolue du nombre  ( + 3 ,2 )  et ( - 3,2 ) .

 

        Lorsque nous voulons connaître ou identifier  la « valeur absolue » d’un nombre relatif , par convention ,  nous encadrons le nombre  par un trait vertical (de chaque coté du nombre).

 

L’ordre donné en mathématique  pour dire :

 «  donner la valeur absolue du nombre  (-3) »se traduit en signe mathématique de la façon suivante : ½ ( - 3 ) ½

(une barre verticale de la hauteur d' une ligne  située de chaque coté du nombre relatif , on dit aussi deux barres encadrant le nombre relatif ….)

                      ½ ( - 3 ) ½                         (la valeur absolue est   3 )

       remarque :pour donner la valeur absolue d’un nombre relatif  il n’y a pas de calcul à effectuer il suffit d’écrire:

                             ½ (+ Vabs) ½    =  Vabs     ; ½ ( -Vabs .) ½   = Vabs.

                    

 Pour obtenir la valeur absolue du nombre relatif, il faut  supprimer les parenthèses  et le signe + du nombre relatif positif  ou le signe  -  du nombre relatif négatif.

 

       Important :Les nombres non relatifs n’ont pas de valeur absolue; par exemple on ne peut donner la valeur absolue du nombre 3,éventuellement ,si l’énoncé le permet il faudra transformer  3 en nombre relatif    (+3)  ensuite il sera possible de prétendre que la valeur absolue de (+ 3) est  3.

 

ATTENTION ; ATTENTION : aux simplifications « abusives »

 

Exemple :

 3,2  est un nombre décimal  et non un nombre relatif ;

 + 3,2 est  l’ écriture simplifiée du nombre relatif positif      ( + 3,2 )

-  3,2 est  l’ écriture  simplifiée du nombre relatif négatif      ( - 3,2 )

 

Exemple : reconnaître  parmi les nombres suivants ceux qui sont positifs et ceux qui sont négatifs ; un seul n’est  pas « relatif » ; lequel ? 

( -5,3) ;  3 ; - 7 ; + 5 ; + 4,8 ; - 3,2 ; 8,9 ; ( +3,2) ; ( -5,3)

réponses :

les nombres relatifs positifs sont : + 5 ; + 4,8 ; 8,9 ; ( +3,2) ;

les nombres relatifs négatifs sont :     - 7 ;  - 3,2 ; ( -5,3)

le nombre qui n’est pas un relatif  positif  est :  3

 

tout au plus : on peut dire que « 3 » est un nombre arithmétique dit « positif »

 

Important  : un alignement  horizontal de chiffres  , seul , non précédé d’un signe + ou – ne peut pas être assimilé à un nombre « relatif positif » ; puis qu’un alignement horizontal de chiffres est déjà appelé « valeur absolue » du nombre relatif .

 

Remarque : le non respect de ces définitions posent des problèmes lorsque l’on veut ( et doit) transformer une expression algébrique en somme algébrique , en vu d’effectuer une suite  d’ opérations avec les nombres relatifs.

Bilan  :

 

Nombres relatifs	Nombre relatif positif	Nombre relatif négatif	Forme simplifiée	Valeur absolue
( + 3,7)	( + 3,7 )		+ 3,7	3,7
( - 3, 7 )		( - 3,7 )	- 3,7	3,7

 

 

Remarque :   On  ne peut pas  assimiler le nombre  « 3,7 » la forme simplifiée   du nombre relatif  positif : + 3,7

Dans les nombres relatifs  , l’alignement de chiffres  séparés ou non par un virgule est la valeur absolue de deux nombres relatif : positif et négatif .

 

B )  l’ Ensemble  «  Z  et  D^{+ ou -} ».

 

           Les nombres utilisés seront les nombres dits « décimaux relatifs »,ces nombres appartiennent à l’ensemble  des nombres décimaux relatifs positifs  ( D ⁺) ou nombres décimaux relatifs négatifs (D ^-).

 La représentation graphique des nombres décimaux relatifs est un ensemble de points alignés  situés sur une droite graduée

avec à gauche du zéro les nombres négatifs  avec 0^-;-1;-2;-3;.......par ordre décroissant ;on dit  jusqu’à « moins l’infini » (symbole: -

 à droite du zéro                les nombres relatifs positifs  (avec 0⁺; +1 ;+2 ;+3;.........), classés par ordre croissant. ,ce jusqu’à plus l’infini (+)

 

C ) Représentation graphique des nombres relatifs:  Voir Obj. REP 1

 

                  La  représentation graphique d’un nombre relatif est  « un  point   » sur une droite graduée ,(une droite graduée prendra le nom :d ’ AXE )

    

         D) Un nombre relatif possède son symétrique  par rapport à « 0 » :

 

Le symétrique de (+ 5)  est (–5)   ;  et le symétrique de  (-5) est (+ 5)

 

On retiendra que La somme de deux nombres relatifs symétriques est égale à « 0 »

 

 

TRAVAUX AUTO  FORMATIFS.

 

« CONTROLE »:

 

              1°) Combien de parties comporte un nombre relatif?  (précisez)

              2°)Quels symboles mathématiques utilise - t - on pour indiquer que l’on veut la valeur absolue du nombre relatif?

             

   « EVALUATION »

 

      1°)   Nommez les trois  parties principales de   (+3)

      2°)  Traduire  : |(+3) |

 

 

INTERDISCIPLINARITE