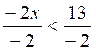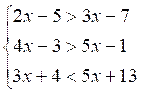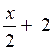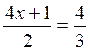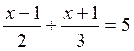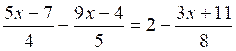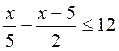|
|
|
Pré requis:
|
|
|
|
@ Formation : Niveau V (inter
actif) |
q |
|
|
ENVIRONNEMENT du
dossier:
|
|
>>>>Liste des cours |
Objectif suivant |
DOSSIER « ALGEBRE » : Le
premier degré.(niveau IV)
Dont : Résoudre un
problème du premier degré à une inconnue.
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
1°)Corrigé
sur les inéquations |
Travaux
|
|
Cours |
Corrigé cours |
Situations problèmes |
||
|
Les équations du premier degré |
|
|
|
||
|
Les inéquations du
premier degré |
|
|
|||
|
|
|
|
|||
|
|
|
|
|
||
|
|
Objectifs :
étude de
situations conduisant à des problèmes
du premier degré. Méthodes de résolution graphique
d’une inéquation à deux inconnues ou
système d’inéquation à deux inconnues et savoir réinvestir dans l’étude de
situations. |
|
|||
|
|
Liste des
chapitres : |
|
|||
|
|
|
|
|||
|
|
|
|
|
||
|
I ) Premier degré
à 1 inconnue : |
|
|
|
|
|
q |
|
|
|
|
|
2°) Résoudre une
inéquation du premier degré à une inconnue. |
q |
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
II ) Premier degré
à 2 inconnues : |
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
q |
|
|
|
|
|
4°) Inéquation du
premier degré à deux inconnues et
régionnement du plan |
q |
|
|
|
|
q |
|
|
|
|
|
6°)Programmation linéaire |
q |
|
|
|
|
|
|
||
|
Pré requis :
définitions Equations et inéquations
du premier degré. |
|
|
|
1°) Equation du premier degré à une inconnue |
A ) si
« ![]() » ¹
, l’équation «
» ¹
, l’équation « ![]() » admet une
solution unique :
» admet une
solution unique : ![]()
B ) Pour résoudre une équation du premier degré
à une inconnue, on regroupe , tous les termes contenant l’inconnue dans un
membre et tous les autres termes connus
dans l’autre membre.
Exemple :
![]()
Résolution
successive : ![]()
RAPPELS :
Avant
de passer à la troisième étape « résolution de l’équation » ;il est nécessaire de faire un rappel sur les propriétés des
égalités (@) :
Définition :
une équation est une égalité qui peut subir
toutes les transformations suivantes :
|
Exemple
1 |
Règle
1 |
|
Soit
l’égalité Ajoutons
5 unités à chaque membre : On
a , encore l’égalité : |
On peut
ajouter un même nombre aux deux membres d’une égalité sans altérer cette
égalité. |
|
Exemple
2 |
Règle
2 |
|
Soit
l’égalité Retranchons
3 unités à chaque membre : On
a , encore l’égalité : |
On peut
retrancher un même nombre aux deux membres d’une égalité sans altérer cette
égalité. |
|
Exemple
3 |
Règle
3 |
|
Soit
l’égalité 8 = 8 Multiplions
par 3 unités chaque membre : 8 × 3 = 8 × 3 On
a , encore l’égalité : 24 = 24 |
On peut
multiplier les deux membres d’une égalité par un même nombre sans altérer
cette égalité. |
|
Exemple
4 |
Règle
4 |
|
Soit
l’égalité Divisons par 2
unités chaque membre : On
a , encore l’égalité : |
On peut
diviser les deux membres d’une égalité par un même nombre sans altérer cette
égalité. |
|
Exemple
5 |
Règle
5 |
|
Soit
l’égalité On
peut retrancher D’autre
part , soit l’égalité : On
peut ajouter 3 unités de chaque côté de l’égalité, et l’on a : |
Si l’on
transporte un terme algébrique précédé du signe + ou - ,
d’un membre d’une égalité dans l’autre membre, ce terme garde sa valeur
absolue, mais change de signe. |
Toutes
les propriétés des égalités s’appliquent aux équations.
|
Exemple
6 |
Règle
6 |
|
Soit
l’équation Divisons
les deux membres par « |
Dans une
équation, pour chasser le coefficient de « x », il suffit de
diviser les deux membres par ce coefficient. |
|
Exemple
7 |
Règle
7 |
|
Soit
l’équation : On
a deux fractions qu’on peut réduire au plus
petit commun dénominateur. Celui - ci est Effectuons la transformation , on a : Multiplions
les deux membres par et la solution est : |
Lorsqu’
une équation présente des dénominateurs différents, on réduit tous les termes
au même dénominateur. On supprime ensuite ce dénominateur commun. Remarque : la
suppression des dénominateurs s’appelle « chasser les
dénominateurs ». |
|
2 ) Résoudre une inéquation du premier
degré à une inconnue. |
Définition : une inéquation est
une relation d’ordre mathématique qui comprend une inconnue en général notée
« x » : Elle comprend les sigles suivants :
|
|
£ |
signifie |
« est
plus petit ou égal à… » |
|
|
|
³ |
signifie |
« est
plus grand ou égal à… » |
|
|
|
> |
signifie |
« est
strictement plus grand que… » |
|
|
|
< |
signifie |
« est
strictement petit que… » |
|
Il faut lire
de gauche à droite… !!!!.
Elle
est du premier degré lorsque la puissance de « ![]() » ne dépasse pas
« 1 »
» ne dépasse pas
« 1 »
Remarque :ne pas
confondre : x 1 =
x alors que x 0 = 1
Résolution :
Résoudre
une inégalité, c’est déterminer pour quelles valeurs de « x » elle
est satisfaite.
On
dit aussi « que c’est trouver toutes les valeurs de l’inconnue pour que l’inéquation
soit vérifiée ». Ces valeurs sont les « solutions de
l’inéquation ».
Exemple :
|
|
|
|
|
|
|
|
Premier membre |
|
Deuxième membre |
|
►Si ![]() , alors ,
le premier membre vaut 4 * 0
- 1 = 0 - 1
= - 1 et le second membre vaut 0 + 2 = 2
, alors ,
le premier membre vaut 4 * 0
- 1 = 0 - 1
= - 1 et le second membre vaut 0 + 2 = 2
comme
- 1 > 2 est « faux » , alors 0 n’est pas solution de
l’inéquation
►
Si ![]() ; alors le premier membre
vaut 4 * 3 - 1 =
12 - 1 = 11 et le second membre vaut 3 +2 = 5
; alors le premier membre
vaut 4 * 3 - 1 =
12 - 1 = 11 et le second membre vaut 3 +2 = 5
comme
11 > 5 est « vrai », alors « 3 » est une solution de l’inéquation
.
On remarque
qu’il y a une infinité de solutions possibles. On parlera donc d’ensemble de
solutions.
Remarque : résoudre une égalité du
premier degré c’est chercher « une » solution ;
alors que résoudre une inégalité c’est chercher « les »
solutions qui vérifient….
Méthode
de résolution
L’ objectif : on veut isoler « x » dans un membre
( généralement dans le premier membre).
Procédure :
transformer l’inéquation avec l’aide des règles suivantes :
|
Règles
|
|
Exemple
|
|
N°1 : en ajoutant ou en
retranchant un même nombre aux deux
membres de l’inéquation. |
Si Si a < b
alors a - c < b -c |
|
|
N°2 :
en multipliant ou en divisant un même nombre positif non nul les
deux membres de l’inéquation. |
Si a > b
alors a * c >
b *c Si a > b
alors a / c > b /c |
a *
5 > b * 5 a / 5 > b / 5 |
|
N°3 : en multipliant ou en divisant un même nombre
négatif non nul les deux membres
de l’inéquation et en changeant le signe de l’inégalité. |
Si a > b
alors a * c < b *c Si a > b
alors a / c < b /c |
a * (-5) <
b * (-5) a / (-5) < b / (-5) |
Remarque :
5 > 3 est vrai si je multiplie
par (-1) les deux nombres : on obtient -5 > - 3 ce qui est faux , je dois changer le signe de la relation d’ordre pour
que cela soit vrai : - 5 < - 3
Remarque : Les théorèmes relatifs aux
inégalités permettent des transformations analogues à celles que nous employons pour les
« égalités »
Ainsi
,on peut, pour les inégalités comme pour les
égalités , faire passer un terme d’un membre dans l’autre en changeant
son signe, et procéder aux
simplifications visibles « a priori » que nous avons indiquées
pour les équations ,à savoir : suppression des termes
identiques dans les deux membres , suppression d’un facteur commun à
tous les termes (à condition que ce facteur soit positif ) , etc.
On pourra aussi
chasser les dénominateurs.
Les inégalités du premier degré à une inconnue se résolvent donc
par une démarche tout à fait semblable à celle que nous avons indiquée pour
les équations, et la règle de résolution
serait aisée à formuler .
Il
faut seulement avoir grand soin de changer le sens de l’égalité lorsqu’on
multiplie ou divise par un nombre négatif.
Si
on multiplie ou si on divise les deux
membres d’une inéquation par un même nombre :
- strictement positif : on conserve le
sens de l’inéquation.
- strictement négatif : on change le sens
de l’inéquation.
|
|
Exemple
n°1 : résoudre l’inéquation 4 x -
1 >
x + 2 1°)
On regroupe les « termes en
x » dans le premier membre en appliquant
la règle n°1 4 x - 1 - x >
x + 2 - x (on retranche « x ») on
réduit : 3 x - 1 > 2 2°)
on regroupe « les termes sans x » dans le second membre en
appliquant la règle 1 3 x - 1 +1 >
+ 2 + 1 (on ajoute « 1 ») on
réduit : 3 x > 3 3°) On isole « x » à l’aide de la
règle 2 (puisque « 3x » est positif) 3 x / 3
> 3 /3 (on
divise par 3 ) On
réduit : x > 1 4°)
conclusion : Les
solutions sont tous les nombres strictement
plus grand que 1 . On note également l’ensemble des solutions (
S ) sous la forme d’un intervalle .Dans ce cas cet intervalle est ] - 1 ; + ¥
[ Tel
que S = ] - 1 ;
+ ¥
[ « + ¥ » se lit « plus l’infini » , ce sont tous les nombres positifs très grands. On
pourrait utiliser la représentation graphique ( axe
gradué) pour montrer les solutions . |
|
|||
|
|
|
|
|||
|
|
Précisions sur la notation des intervalles de
nombres : |
|
|||
|
|
|||||
|
Intervalles |
Lire : |
Traduire : |
|||
|
[ 2 ;
5 ] |
:intervalle 2 ; 5 fermé, ce sont tous les nombres
« |
|
|||
|
|
: intervalle
2 fermé ; 5 ouvert, ce sont tous les nombres « |
|
|||
|
|
: intervalle
2 ; 5 ouvert, ce sont tous les nombres « |
|
|||
|
|
Ce sont tous les
nombres « |
|
|||
|
|
Ce sont tous les
nombres « |
|
|||
|
|
Ce sont tous les
nombres « |
|
|||
|
|
Ce sont tous les
nombres « |
|
|||
|
|
|||||
|
|
Soit , par exemple n°2 : Résoudre l’inégalité :
on fait passer les
termes renfermant les « x » dans le premier membre et les autres
dans le second membre, elle devient :
d’où
en divisant par
on doit
changer le signe « > » en « < » x <
|
|
|||
|
On
a changé le sens , puisque
–2 est négatif. |
On conserve le sens de l’inéquation si l’on multiplie ou si on divise
les deux membres d’une inéquation par un nombre strictement positif.
On
change le sens de l’inéquation si on multiplie ou si on divise les deux membres
d’une inéquation par un même nombre
strictement négatif.
Exemples :
a)
Résoudre : ![]()
on divise par « 4 » : ![]()
Conclusion L 3 façons ou formes peuvent être utilisées
pour conclure)
Première forme (l’inégalité): ![]()
Deuxième forme (l’intervalle) : ![]()
Troisième forme :
Par le représentation
graphique :
|
|
|
|
la partie hachurée représente les non solutions ; la
partie à gauche de « ![]() » représente l’ensemble des solutions
, valeurs que peut prendre «
» représente l’ensemble des solutions
, valeurs que peut prendre « ![]() ».
».
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b )Exemple : Résoudre : On
divise par « Conclusion : Première forme Deuxième forme : Troisième forme : représentation
graphique : |
|
|
|
|
|
|
|
la partie hachurée
représente les non solutions ; la partie à droite de « - 2,5 »
représente l’ensemble des solutions , valeurs que
peut prendre « |
|
Activités :
Donner
les solutions des inéquations suivantes sous forme d’intervalle :
|
|
|
|
|
|
|
|
|
|
|
3°) Résolution
d’un problème du premier degré à une inconnue |
La résolution d'un problème par l'algèbre peut se
décomposer en quatre parties:
1°) choix de la ou des inconnues
2°) mise en équation
3°) résolution des équations
4°) discussion du problème
Exemple
de problème :
|
Enoncé
|
|
|
On
veut partager une somme de 60 000 € entre trois héritiers, de manière
que le deuxième ait 5 000 € de plus que le premier, et le troisième
1 000 € de moins que le deuxième. Calculer la part de chacun. |
|
1°) Appelons « x » la part du premier.
2°)
On a :
Part
du premier : ![]() ;
;
Part
du deuxième : ![]()
Part
du troisième :
![]() ou
ou ![]()
Il
est évident qu’on obtient l’équation :
![]()
3°) on a à résoudre l’équation trouvée :
![]()
On
gardera tous les « ![]() » du même côté
de l’égalité, ce qui fera «
» du même côté
de l’égalité, ce qui fera « ![]() », et l’on fera
passer les nombres
», et l’on fera
passer les nombres ![]() et
et ![]() du côté opposé. D’après les règles
précédentes, on aura :
du côté opposé. D’après les règles
précédentes, on aura : ![]()
![]()
![]()
4°)
La part du 1er héritier sera de 17 000 €
Le 2e héritier aura : 17 000 + 5 000 =
22 000 €
Le 3e héritier aura
22 000 - 1000 = 21 000 €
Commentaire : le résultat
est positif et devaient l’être forcément.
Vérification : ![]()
Remarque :
ici , l’équation était « simple » , et ne
présentait aucun dénominateur à faire disparaître.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4°)
Résoudre un système d’inéquations du premier degré à une
inconnue. |
|
|
Résoudre un système d’inéquations : Résoudre un
système d’inéquations ( dit aussi inéquations simultanées)
à une inconnue, c’est trouver les valeurs de cette inconnue qui satisfont à la fois à toutes ces inéquations. Pour
résoudre un tel système , il
suffit de résoudre successivement toutes les inéquations données et de conserver les solutions communes. Pour cela,
si le résultat n’est pas immédiat, il peut être commode de ranger par ordre de grandeur croissante les valeurs limites
trouvées. On détermine ainsi un
certain nombre d’intervalles. On barre ceux dans lesquels l’inconnue ne doit pas se trouver. Les intervalles non barrés donnent les solutions
du système. Exemple :
résoudre le système : |
|
|
|
|
|
|
|
De la
première : 1ère
équation : le résultat donne : De la 2ème
équation : De la
troisième 3ème
équation Le résultat est
immédiat :
|
|
|
|
Voir la
solution graphique :
tracer 3 droites graduées |
|
|
|
|
|
|
|
|
|
|
|
|
A) Equation du premier degré à deux inconnues |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ecriture : l’équation du premier degré à 2 inconnues peut se mettre sous la forme
« a x + by + c = 0 »
Exemples : 3 x - 5 y + 4 = 0 ; 2x
+ y - 3 = 0
Dans
l’étude de système d’équations , l’équation se met
sous la forme : a x + by = c
Exemples :
3 x - 5 y + 4 = 0 s’écrira 3x
- 5 y = - 4
2x + y - 3 = 0 s’écrira 2x
+ y = + 3
Dans
un système à deux équations on retrouvera l’écriture : 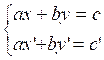
|
B)
SYSTÈME DE DEUX ÈQUATIONS
À DEUX
INCONNUES : |
Soit
le système 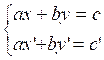
Résoudre
ce système, c’est trouver les solutions communes aux deux équations qui le
composent.
Pour
résoudre un système on peut utiliser
3 méthodes : 2 méthodes
par résolution algébrique et
une méthode par résolution graphique.
Résolution
algébrique : Pour ces deux méthodes , on forme à
partir du système donné, une équation contenant une seule inconnue. Il
faut donc faire disparaître ou « éliminer » l’autre inconnue.
|
|
|
|
|
|
|
|
|
|
|
|
Cette
méthode consiste à exprimer une inconnue « en fonction » de l’autre
dans une équation et à substituer l’expression trouvée (la valeur ainsi trouvée) dans l’autre équation.
Exemple :
Résoudre
le système ( I )
suivant :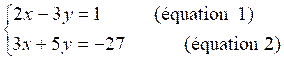
1°)
transformation de l’équation (1) :
2x - 3 y = 1 devient y = 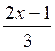 (3)
(3)
Toute solution du système (I) est solution du
système (II):
système ( II ) 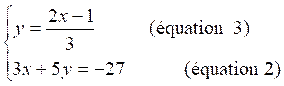
2°)
Remplacement de l’équation (3) dans
l’équation (2)
3 x + 5 (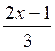 ) = - 27 ;
) = - 27 ;
après développement
on obtient 9x + 10 x - 5 = - 81
soit après regroupement : 19 x = - 76
ainsi : x = - 4
recherche de la valeur de « y » connaissant
celle de « x »
si y = 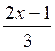 et x = -4 ; alors y =
et x = -4 ; alors y = 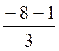 = - 3
= - 3
Conclusion : si le
système admet une solution, c‘est :
x = - 4 ; y = - 3
Vérifions
par le calcul qu’il
en est bien ainsi : (pour
x = - 4 ;et pour ; y= - 3)
Dans
l’ équation 2x
- 3y = 1 ; 2 × ( -4) - 3 ( -3 ) =
+1
Dans
l’équation 3x + 5 y = - 27
; 3 ( -4)
+ 5(-3) = - 27
Vérifions
par le tracé :
il faut tracer la droite ( D1 )
d’équation y1 = 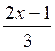 et la
et la
droite ( D2
)d’équation : y2 = 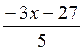 ; le point
d’intersection des deux droites est
; le point
d’intersection des deux droites est
solution
du système soit le point de coordonnés ( - 4 ; -
3 ) . A VERIFIER !!!!
|
|
|
|
|
|
|
|
|
|
|
|
Cette
méthode consiste à ajouter membre à membre les deux équations après
multiplication par un facteur adapté, de façon à éliminer l’une des deux
inconnues.
Exemple :
résoudre le système 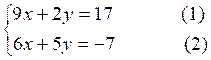
Les
coefficients de « y » sont +2 et +5. Nous pouvons les rendre
symétriques en multipliant les deux membres de la première équation par
« 5 » et ceux de la seconde par « -2 » ; Nous
obtenons :
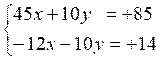
En
additionnant, on obtient : 33x = 99 ; soit x = 3
Remplaçons
« x » par « 3 » dans l’équation (1)
27 + 2y = 17
ou 2y = - 10 soit y = -5
On
vérifie que : x
= 3 ; et y = -5 est bien solution du système
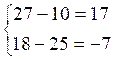
En
conclusion la méthode de l’addition consiste à multiplier les deux membres de
chaque équation par des « multiplicateurs » de façon que les
coefficients d’une inconnue deviennent symétriques. On élimine cette inconnue
par addition.
|
|
|
|
|
|
|
|
|
|
|
|
Chaque
équation du système est transformée
de manière à être interprétée comme une
équation de droite.
Résoudre
un système « par le graphique » revient à déterminer les coordonnées
du point d’intersection de deux droites.
Exemple1 :
résoudre graphiquement le système 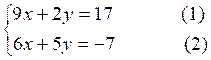
Exemple
2 : Résoudre graphiquement le système :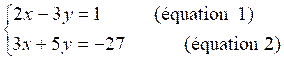
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Définition :lorsqu’un problème conduit à la résolution d’un système de
plusieurs équations du premier degré , on dit encore que c’est un problème du premier degré.
La
marche à suivre pour résoudre ces problèmes est analogue à celle utilisée pour
un problème à une inconnue, c’est à dire :
1°)
On choisit les inconnues ;
2°)On met le problème en équation.
3°)
On résout le système d’équations obtenu ;
4°)
On discute,
c’est à dire qu’on regarde si la solution obtenue satisfait aux différentes
conditions qui doivent vérifier les inconnues.
|
1°) Problème résolu. :à
deux inconnues |
@ |
|
|
|
|
|
|
|
|
|
|
|
|
Un
cycliste parcourt un trajet AB qui comporte uniquement des montées et des
descentes. Les vitesses moyennes sont de 10 km/h en montée et 30 km/h en
descente. Dans le sens A vers B il met 4
h 20 mn , dans le sens de B vers A il met 5h. On
demande la longueur des montées et des descentes dans le sens A vers B.
Résolution :
Soient
« x »la longueur des montées, et « y » celle des descentes
dans le sens A vers B, ces longueurs étant évaluées en kilomètres.
La
mise en équation est immédiate. On doit avoir :
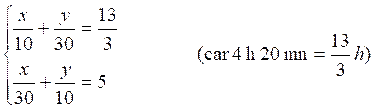
c’est à dire : 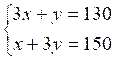
En
procédant par exemple par addition on obtient : 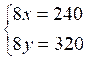
D’où :
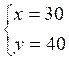
Discussion :pour les valeurs trouvées soient acceptables, il faut et il
suffit qu’elles soient positives. Ces conditions sont réalisées et les
distances cherchées sont 30 km et 40 km.
|
2°)
Problème résolu à trois inconnues. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Un
cycliste parcourt un trajet AB qui comporte des montées ,
des paliers et des descentes. Les vitesses
sont 10 km/h en montée ; 20 km/h en palier ; 30 km/h en descente.
Dans le sens AB il met 6 h 50mn ; dans le sens BA il met 7 h 30 mn. Le
trajet AB comportant 120 km, on demande la longueur des montées, des paliers , des descentes.
Résolution :
Désignons
par « x » la longueur totale des paliers, par « y » celles
des montées dans le sens A B, par « z » celle des descentes, ces
distances étant exprimées en km. Exprimons les temps en heures, donc les
vitesses en kilomètres - heure.
La distance AB est 120 km : x + y + z = 120
La
durée du trajet AB est 6 h 50 m n , soit 6 h ![]() ou
ou ![]() d ’heure :
d ’heure :
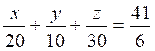
Dans
le sens BA , les montées deviennent descentes et les
descentes deviennent montées. La durée du trajet BA est
7 h ![]() , soit
, soit ![]() heures.
heures.
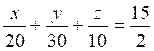
Nous
sommes conduits à résoudre le système suivant :
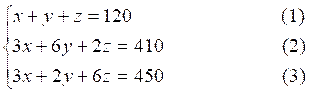
Pour
résoudre ce système, formons un système de 2 équations à 2 INCONNUES. Pour cela
nous éliminons « x » entre (2) et (3) : 4 y - 4z = - 40
Eliminons
« x » entre (1) et (3)
|
|
-3 x - 3 y - 3z = -
360 3x +
2y + 6 z = 450 |
|
|
|
0 x -
y +3z =
90 |
|
On
obtient :
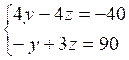 Þ
Þ 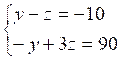 Þ
Þ
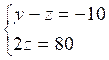
Donc :
z = 40 et y = 30 et en substituant dans
(1) : x = 50
On
pourra vérifier que cette solution convient au problème. IL y a donc dans le
sens AB ; 50 km de paliers ; 30 km de montées et 40 km de descentes.,
|
D )
Inéquation du premier degré à deux inconnues et
régionnement du plan : |
Ecriture : l’inéquation du premier degré à 2 inconnues peut se mettre sous la
forme
|
« a x + by + c > 0 » |
Lire : strictement supérieur à 0 |
|
« a x + by + c < 0 » |
Lire : strictement inférieur à 0 |
|
« a x + by + c "e 0 » |
Lire : strictement supérieur ou égal à 0 |
|
« a x + by + c "d 0 » |
Lire : strictement inférieur ou égal à 0 |
Exemples : 3 x - 5 y + 4 > 0 ; 2x
+ y - 3 < 0
Dans
l’étude d’une inéquation ou d’un système d’inéquations ,
on trouvera l’écriture sous la
forme :
a x + by "e c ou : a x + by "d c
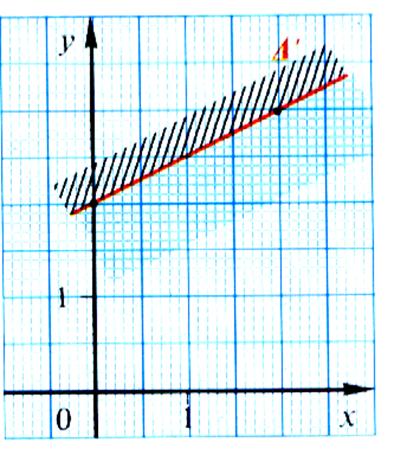
Exemple : résoudre
graphiquement : x - 2y + 4 >
0
Objectif :
on recherche tous les points dont les coordonnées vérifient l’inégalité.
|
On
transforme successivement pour obtenir
une inéquation de la forme : y
…. %Ï On transforme
l’inéquation : x - 2y + 4 > 0 - 2y > -x - 4 2y <
x + 4 y < %Ï On trace la droite d’équation : y = %Ï Recherche de la zone (1/2 plan qui
convient): On
essaye
l’origine ( 0 ; 0), remplaçons
ces valeurs dans l’équation : y < 0 < 0 +
2 cette
inégalité est vraie. conclusion :
tous les points du demi- plan qui contient l’origine vérifient l’inégalité. On
hachure le demi plan qui ne convient pas. (on peut colorier le demi -plan qui
convient) |
|
|
E) SYSTEMES D’INEQUATIONS du premier degré à deux
inconnues. |
|
|
|
|
|
|
|
|
|
|
|
|
Nous nous bornerons à une méthode graphique.
Celle -ci résulte immédiatement. Du théorème énoncé (cours :
définition)):
La droite (D) qui a pour
équation a x
+ by + c = 0 partage le plan en deux
régions.
Pour
tous les points de l’une on a : a x + by + c > 0
Et
pour tous les points de l’autre : a x + b y + c < 0
Le
théorème réciproque se démontre immédiatement par l’absurde. On en conclut que
les relations précédentes sont « caractéristiques » des points des
deux régions que détermine la droite « D ».
Exemple :
résoudre le système :
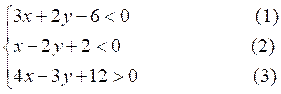
Etant
donnés deux axes de coordonnées Ox ; Oy ; nous allons déterminer dans quelle région du plan
se trouvent les points « M » dont les coordonnées satisfont à ces
trois inéquations.
Pour
cela nous construisons les droites qui ont respectivement pour équations :
3 x + 2y - 6
= 0 ( D)
x -
2y + 2 = 0 ( D’)
4x - 3y +12
= 0 ( D’’)
Pour
que l’inéquation (1) soit satisfaite il faut et il suffit que « M »
soit dans la région qui contient l’origine ( car pour
x = 0 ; y = 0 l’inéquation est satisfaite ).
Pour
que l’inéquation (2) soit satisfaite il faut et il suffit que « M »
soit dans la région qui ne contient par l’origine ( car
pour x= 0 ; y = 0 l’inéquation n’est
pas satisfaite).
Enfin
pour que l’inéquation (3) soit satisfaite il faut et il suffit que
« M » soit dans la région qui contient l’origine (
car pour x = 0 ; y = 0
l’inéquation est satisfaite).
TRACER :
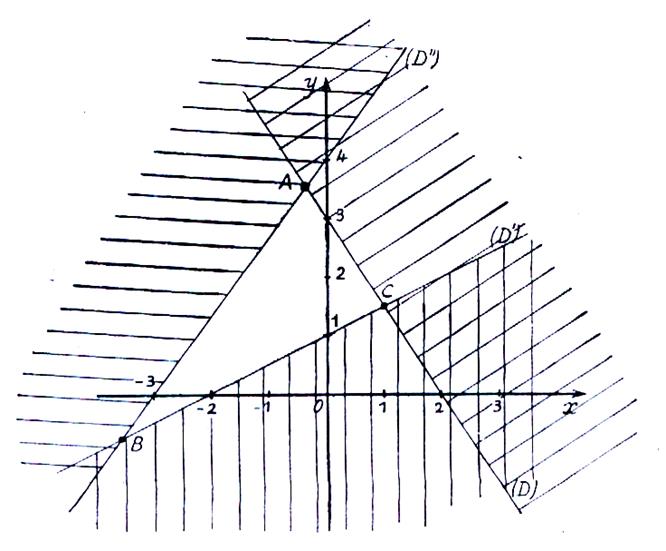
Finalement , on voit que M doit être à l’intérieur du
triangle ABC formé par les 3 droites ( D
) ; (D’) ; (D’’).
|
|
|
|
|
|
|
|
|
|
|
|
Résumé du cours :
A ) Equation du premier degré :
1°)
Equation du premier degré
à une inconnue :
a x = b , avec
« a » non nul , la solution est
x = ![]()
2°)
SYSTÈME DE DEUX ÈQUATIONS
À DEUX INCONNUES :
![]() Pour résoudre un système de deux équations à deux inconnues
on dispose de trois méthodes :
Pour résoudre un système de deux équations à deux inconnues
on dispose de trois méthodes :
2
méthodes « algébrique » : dites
l’une « par
substitution » , l’autre par
« combinaison ».
la troisième est
appelée : « méthode graphique »
B ) Inéquation du premier degré :
Premier
cas :
si a > 0 , on conserve le sens de
l’inégalité :
![]() Û
Û ![]() Û
Û ![]()
deuxième
cas :
si a < 0 , on change le sens de l’ inégalité
![]()
|
Inéquation
du premier degré à deux inconnues : |
Soit
l’équation ![]()
Par
transformation elle devient la droite
« D » d’équation 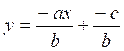 , cette droite
partage le plan en deux demi-plans de « frontière » « D »
tels que :
, cette droite
partage le plan en deux demi-plans de « frontière » « D »
tels que :
-
Pour tout point M ( x ;
y) de l’un , a x + by "e c ;
-
pour tout point M (x ; y ) de
l’autre a x + by "d c
Pour
sélectionner le demi-plan recherché, on
teste un point quelconque M ( xM ;yM ) du
plan n’appartenant pas à la droite.
Très
souvent ; par commodité,pour
éviter les calculs , on choisit
l’origine « O ».
Ainsi
on analyse le résultat :
0x + 0 y
( ?) "e c ou
0x + 0 y ( ?) "d
c
la solution est donnée au cas par cas !!!!!!
|
Système
d’inéquations du premier degré à une
inconnue : |
En
général, on résoudre « graphiquement » ce genre de système.
Résoudre
graphiquement un système d’inéquation,
c’est rechercher la partie du plan commune aux demi- plans représentant chacune
des inéquations du système.
|
|
TRAVAUX AUTO - FORMATIFS |
|
|
|
|
|
|
|
(Travaux servant de préparation et de
support à un devoir sur feuille) CONTROLE : 1°) citer les 7 règles permettant de résoudre les équations du premier
degré à une inconnue. 2°) Donner la procédure de résolution d’un problème (par l’algèbre): (Citer les 4 étapes chronologiques de
la résolution d’un problème d’algèbre : Premier degré : EQUATION. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Résoudre : |
Résolution |
|
1-a |
|
|
|
1-b |
|
|
|
1-c |
|
|
|
1-d |
|
|
|
1- e |
|
|
![]()
Premier
degré : INEQUATION.
|
|
Résoudre : |
Résolution |
|
1-a |
5x - 7 "e 1 |
|
|
1-b |
-2x + 2 < 5,7 |
|
|
1-c |
8 ( 6x + 3) > 2x |
|
|
1-d |
|
|
Réponses @:
x "d ; x
"e
1,5 ; x > ![]() ; x >
; x > ![]()
Série 1 : (traités dans le cours)
|
Enoncé
du problème N°1 |
|
|
On veut
partager une somme de 60 000 € entre trois héritiers, de manière que le
deuxième ait 5 000 € de plus que le premier, et le troisième 1 000
€ de moins que le deuxième. Calculer la part de chacun. |
|
|
Enoncé
du problème N°2 |
|
|
Une
marchande apporte au marché un panier de pommes ; elle vend d’abord le Combien
avait-elle de pommes ? |
|
|
Enoncé
du problème N°3 |
|
|
Un jardin
rectangulaire de 50 mètres de long est plus grand de 257 mètres carrés qu’un
autre de même forme, d’une longueur de 42 mètres et dont la largeur surpasse
celle du premier de 1, 50 mètre. Calculer la largeur du premier terrain. |
|
|
Enoncé du
problème N°4 |
|
|
Un père
a 38 ans, son fils a 14 ans . On demande dans
combien d’années le père aura juste 3 fois l’âge de son fils. |
|
Série 2.
|
1°) Un
fermier porte au marché un certain nombre d'œufs , qu'il
compte vendre 100 centimes pièce ; il en casse 6 , mais il trouve à vendre
les autres 150 centimes pièce et
rapporte ainsi chez lui 10 francs de plus qu'il ne comptait en partant.
Combien avait-il d'œufs? |
|
Pb N°2 : Un
marchand de vin désire obtenir 100 litres de vin lui revenant à 5 francs le
litre en mélangeant du vin qui lui coûte
3,50 francs le litre avec du vin qui lui coûte 9,50 francs le litre.
Combien doit-il prendre de litres de vin de chaque espèce? |
|
Pb N°3
: Un voleur s'est emparé d'une bicyclette et s'enfuit sur une route avec une
vitesse de 20 km à l'heure ; on s'en aperçoit 3 minutes après son départ et
un bicycliste s'élance à sa poursuite avec une vitesse de 22 km à l'heure .Au
bout de combien de temps le rattrapera-t-il ? (les vitesses sont des vitesses
moyennes) |
|
Pb N°4: Un père
a 40 ans et son fils en a 16 ; quand l'âge du père sera-t-il triple de celui
du fils ? |
Système
d’équations :
Pour un
concert de jazz, les places valent 3 € et 13 € .
Une association
a acheté 32 places pour un montant total de 272 €.
Combien
de places de chaque sorte l’association a - t- elle
acheté ?
Résoudre
le système d’inéquations suivant :
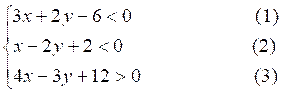
Voir
cas par cas !!!!dans les info +++
EVALUATION:
Corrigé :
Activités sur les inéquations:
Donner les solutions des inéquations suivantes sous forme
d’intervalle :
|
5x + 2 > - x - 4 |
3x + 8 > 5 |
- 4 x + 2 > 0 |
7x - 4 < 18 |
|
x > -1 l’intervalle de « x » solution de cette inéquation est ] - 1 ; + ¥[ |
x > - 1 l’intervalle de « x » solution de cette inéquation est ] - 1 ; + ¥[ |
x < 0,5 l’intervalle de « x » solution de cette inéquation est ] - ¥ ;
0,5 [ |
x <
22/7 l’intervalle de « x » solution de cette inéquation est ] - ¥ ; 22 / 7 [ |