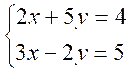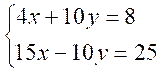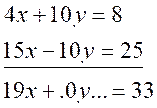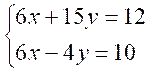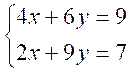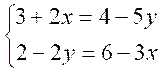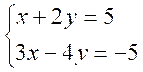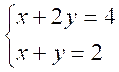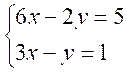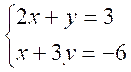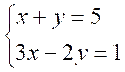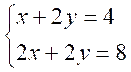Pré requis:

ENVIRONNEMENT du dossier:

Objectif précédent :

Objectif suivant :

les résolutions des systèmes deux équations …..

Liste de cours sur les résolutions d’un système d’équations à deux inconnues..

DOSSIER : Résolution d’un SYSTEME de deux EQUATIONS du PREMIER DEGRE A DEUX INCONNUES par addition (dit aussi par COMBINAISON )

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

SYSTEME DE DEUX EQUATIONS A DEUX INCONNUES.

Deuxième méthode : Méthode de substitution.

Il est parfois avantageux , pour la résolution des systèmes d’équations , d’utiliser une autre méthode dite d’élimination par addition ou soustraction , dont quelques exemples nous montrerons le mécanisme.

Exemple 1

Résoudre le système :

Nous nous proposons d’éliminer »y ».

Si les coefficients de cette inconnue « y » étaient égaux en valeur absolue, on conçoit qu’en additionnant ou retranchant membre à membre les deux équations du système selon que ces coefficient seraient de signes contraires ou de même signe , on obtiendrait une équation ne renfermant plus de « y » , c’est à dire une équation du premier degré à une seule inconnue « x » que l’on saurait résoudre. La méthode que nous choisissons consiste précisément à multiplier les deux membres de chaque équation par des multiplicateur convenablement choisis pour que les coefficients de l’une des inconnues deviennent égaux en valeur absolue.

Premier cas : on élimine « y »

Il suffit, par exemple, de multiplier dans notre système les deux membres de la première équation par 2 et les deux membres de la seconde par 5 , on obtient le système équivalent :

en additionnant membre à membre ces deux nouvelles équations on obtient :

cette dernière équation ne renferme pas « y », on dit que l’inconnue « y » a été éliminée.

On en déduit : x =

Deuxième cas : on élimine « x ».

Prenons maintenant les multiplicateurs 3 pour la première équation et 2 pour la seconde , on obtient par une démarche analogue :

et , en retranchant membre à membre la dernière de ces équations de la précédente , on élimine « x » , et on obtient : 19 y = 2

d’où y =

on en déduit que x =

D’ où nous obtenons pour solution le couple de valeurs ( ; )

Exemple 2

Résoudre le système :

On multipliera la deuxième équation par –2 pour éliminer « x »

On calculera le .PPCM de 6 et 9 ( soit 18) si l’on veut éliminer « y »

la solution est x= et y =

PROCEDURE PERMETTANT DE RESOUDRE UN SYSTEME DE DEUX EQUATIONS DU PREMIER DEGRE A DEUX INCONNUES.

Pour résoudre un système de deux équations du premier degré à deux inconnues il faut :

1°)multiplier les deux membres de chaque équation par des multiplicateurs convenablement choisis de manière que les coefficients de l’une des inconnues , deviennent égaux en valeur absolue ;

2°) On additionne ou retranche membre à membre les deux nouvelles équations , selon que les coefficients de « x » ou « y » sont de signes contraires ou de même signe , on obtient ainsi une équation du premier degré à une inconnue , qu’il est aisé de résoudre .

3°)Pour obtenir « y » ou « x » , on opère sur les coefficient de « x » ou « y » , comme on vient de le faire pour les coefficients de « y » ou « x »

les multiplicateurs s’obtiennent en prenant les quotients du p.p.c.m. des coefficient de l’inconnue à éliminer par ces coefficients.

TRAVAUX AUTO FORMATIFS.

CONTROLE :

Donner la procédure permettant de résoudre un système de deux équations à deux inconnues « x » et « y » par la méthode de combinaison.

EVALUATION

Résoudre le système
Résoudre le système
Résoudre le système
Résoudre le système
Soit le système : rechercher la solution par représentation graphique.

INTERDISCIPLINARITE