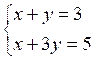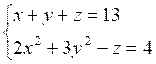|
Savoir transformer des équations de la forme « a x + by +c =
0 » |
|
|
Inéquation du
premier degré à deux inconnues |
|
|
Les Segments et
droites graduées |
|
|
Les intervalles |
|
|
Les demi droites |
ENVIRONNEMENT du
dossier:
|
Objectif précédent : |
Objectif
suivant : 1°)Les différents
moyens de résolution du système . 2°) lecture :
système d’inéquation du premier degré à une inconnue 4°) Systèmes et « fonctions affines et situations
problèmes » |
1°) Voir liste sur le repérage. 2°) Voir liste de travaux basiques en algèbre. 3°)liste des cours de base
sur le système d’équations du ….. et : |
Présentation des ( 3 + 1) ;
4 méthodes de résolution des SYSTEMES d’ EQUATIONS du
premier degré à deux inconnues
« x » et « y »:
I)
DEFINITIONS.
-
a) SYSTEME DE DEUX EQUATIONS A DEUX
INCONNUES.
- b)
Systèmes équivalents.
- c)
« Résolution » ou « recherche de Solutions du
système » ou « racines »
II)
LES
METHODES de résolutions...
|
A ) Par substitution |
|
|
B ) Par combinaison. |
|
|
C ) Par résolution graphique |
|
|
D) Par le calcul matriciel |
dont : recherche d'un "point
commun" à deux droites.
|
COURS |
|
I ) DEFINITIONS.
-
a) SYSTEME DE DEUX EQUATIONS A DEUX
INCONNUES.
|
Un système de deux équations à deux
inconnues : Peut toujours se ramener à la forme
générale : a ; b ;c ; a’ ; b’ ;c’ sont des nombres
réels, « x » et « y » sont les
inconnues. Résoudre un tel système ,
c’est rechercher les valeurs de « x » et de « y » qui
vérifient simultanément les deux équations.et
« x » et « y » sont les solutions ou
« racines » du système. |
- b)
Systèmes équivalents.
On dit que
deux systèmes sont équivalents lorsqu’ils admettent les mêmes solutions
, c’est à dire lorsque toute solution du premier est solution du second
et que toute solution du second est solution du premier.
Remarque : la méthode suivi pour
résoudre une équation du premier degré à une inconnue revient
au fond à remplacer cette équation par une équation équivalente plus
simple ; de même pour résoudre un système d’équations du premier degré à
plusieurs inconnues, on cherche à le remplacer par un système équivalent
plus simple.
- c)
« Résolution » ou « recherche de Solutions du
système » ou « racines »
On appelle « solution du
système » les nombres qui vérifient
à la fois toutes les équations du
système.
|
Par
exemple, le système :
admet
la solution x = 2 ; y =1 il suffit de
vérifier ! ! ! !
que 2 + 1 = 3 ; et que 2
+ 3 fois1 =5 |
|
Autre
exemple : Le
système :
admet
la solution : x
=1 ;y =2 ; z = 10 |
-
d) Résolution d’un système du premier
degré à deux inconnues :
Soit le système 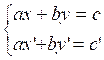
Pour
résoudre un système on peut utiliser
3 méthodes : 2 méthodes
par résolution algébrique et
une méthode par résolution graphique.
II ) LES 3
METHODES DE RESOLUTION d’un système……..
|
A) Par substitution |
Cette
méthode consiste à exprimer une inconnue « en fonction » de l’autre
dans une équation et à substituer l’expression trouvée dans l’autre équation.
|
B) Par combinaison. |
Cette
méthode consiste à ajouter membre à membre les deux équations après
multiplication par un facteur adapté, de façon à éliminer l’une des deux
inconnues.
Remarque
sur le choix d’une des deux méthodes :
Les
méthodes par substitutions et par addition s’appliquent dans le cas d’un
système quelconque d’équations du premier degré, quel que soit le nombre des
équations et le nombres des inconnues.
Il
existe toutefois entre ces deux méthodes
une différence essentielle.
On
démontrera comme dans le cas d’un système à deux inconnues lorsqu’on procède
par substitution on obtient un système équivalent ; il est
donc inutile de vérifier.
Au
contraire, lorsqu’on procède par addition, l’équivalence du système
proposé et du système obtenu n’ayant pas été démontrée ,
on devra vérifier.
|
C) Résolution graphique |
Chaque
équation du système est transformée
de manière à être interprétée comme une
équation de droite.
Résoudre
un système « par le graphique » revient à déterminer les coordonnées
du point d’intersection de deux droites.
Combien y - a - t- il de
méthodes de résolution d'un système d'équations du premier degré à deux inconnues ?
INTERDISCIPLINARITE : Etudes de graphiques ![]()