|
|
|
ENVIRONNEMENT
du dossier:
|
Objectif
précédent : |
Objectif
suivant : |
||||
|
|
|||||
|
|
DOSSIER : LE CUBE : calculs du volume et Aire |
|
|||
|
|
|
|
|||
|
|
I
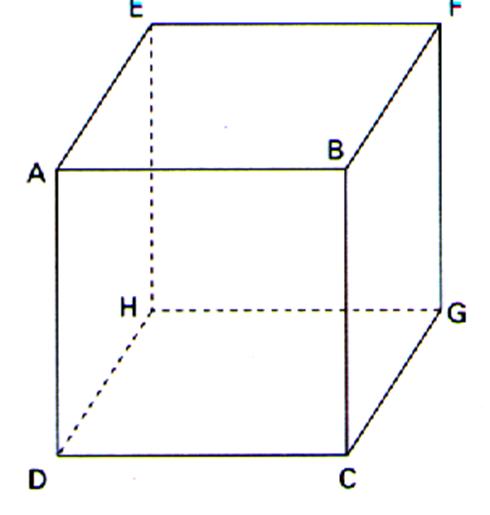
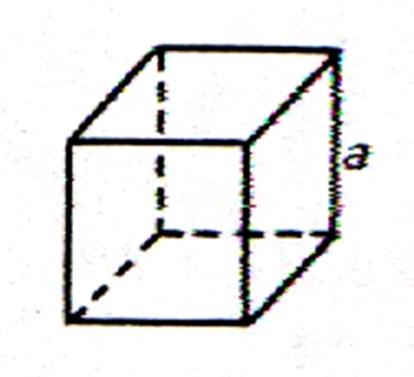
) Représentation d’un cube en perspective. |
|
|||
|
|
II
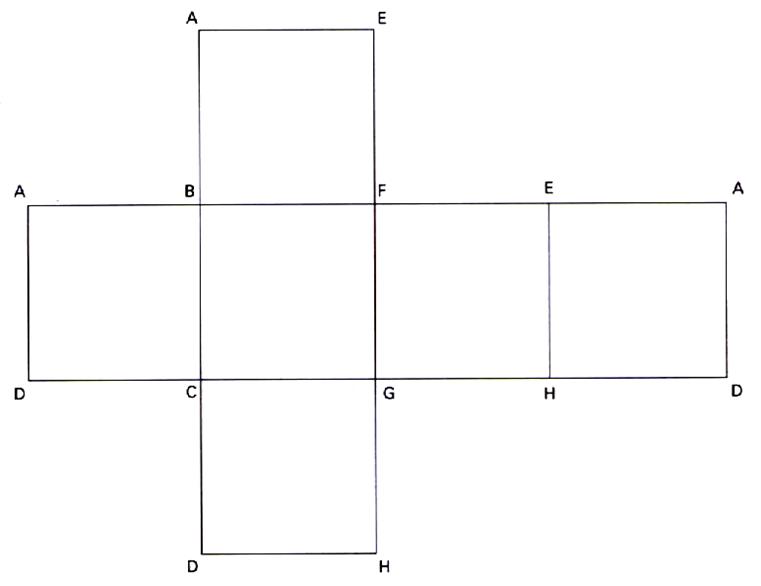
) Développement du cube . et calculs des aires . |
|
|||
|
|
III
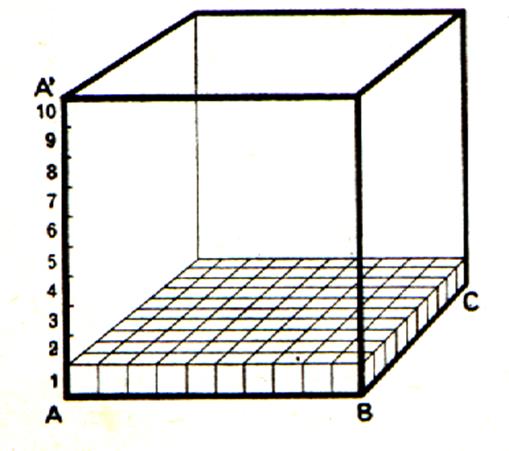
) VOLUME : |
|
|||
|
|
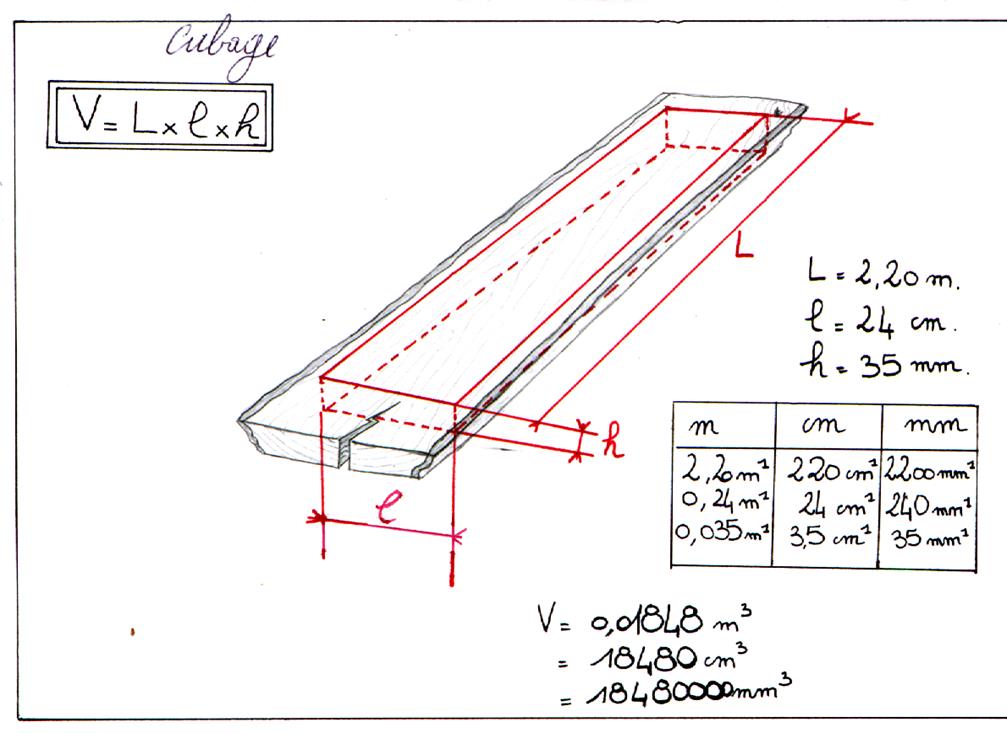
IV ) CUBAGE |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
TEST |
COURS |
|
|
||||
|
|
|
|
Travaux niv
VI et V: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Photo :warme. DINANT
_Belgique_2000 |
|
||
|
|
INFO COURS
|
|
|
|
Tel
qu’il est dessiné le cube est posé sur
sa base DHGC ; son autre base est AEFB :
Les faces latérales : sont ABDC (vue de face ) Les vues de coté sont celle : De gauche : EADH De droite BFGC Et d’arrière : EFGH ou ( FEHG) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I ) Calcul de l’aire de la surface latérale :
l’aire de la surface latérale est égale à 4 fois le « carré » de
son arête. Formule :
4 fois l’aire d’un carré = 4 a2 ( « a » étant la longueur d’une arête) Application : Un cube à Résolution : A = 4 a2 soit : 4 II ) Aire de la surface totale : l’aire de la
surface totale est égale à 6 fois le
« carré »
de son arête. Formule :
6 fois l’aire d’un carré = 6 a2 ( « a » étant la longueur d’une arête) Application : Un cube à Résolution : A = 6 a2 soit : 6 |
|
|
|
|
|
|
|
III
) VOLUME : |
|
|
|
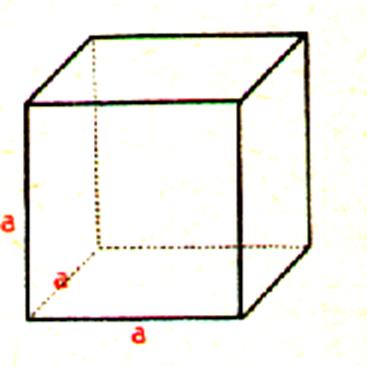
Le
volume d’un cube est égal au produit
de 3 facteurs égaux à
son arête ; en d’autres termes , il est
égal à la 3 e puissance
de son arête : |
|
|
|
On dit aussi : |
|
|
|
Le volume d’un cube s’obtient en multipliant le nombre qui mesure
l’aire de l’une des quelconque de ses faces par le nombre qui mesure le coté de ce cube .
|
|
|
|
Ou encore : le volume d’un cube est égal au cube du nombre qui
mesure son coté . |
|
|
|
|
|
|
|
Application : Calculer le volume d’un cube de
6 dm d’arête égale : Résolution : V = a 6 NIVEAU plus : 1 ) Pour obtenir la longueur de l’arête d’un
cube , si l’on connaît la surface d’une face
, il faut faire la racine carrée
( SOS
Cours ) Exemple
la surface d’une face d’un cube à une aire de
144 dm2 ; quelle est la longueur de son arête ? On fera :
a = 2 ) Pour obtenir la longueur de l’arête d’un
cube il faut faire la racine cubique du volume. ( SOS Cours ) Exemple
le volume d’un cube est de 216 dm3 ; quelle est la longueur
de son arête ? On fera :
a = |
|
|
|
|
|
|
|
TRAVAUX
AUTO FORMATIFS |
|
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
CONTROLE : Calculs : 1 )A
quoi est égale l’aire de la surface latérale d’un cube (donner une
formule) ? 2 ) A
quoi est égale l’aire de la surface totale
d’un cube ? 3) A quoi est égal le volume d’un cube (donner une formule ? 4 )
Donner la formule permettant de calculer le volume d’un cube . EVALUATION Exercices : 1 ) Un
cube à 2 ) Un cube à 3 )
Calculer le volume d’un cube de 6 dm
d’arête égale : 4 ) Compléter
le tableau
5)
INTERDISCIPLINARITE 1 ) Un tas
de briques à la forme d’une cube de 2 ) Une citerne d’eau de forme cubique mesure Quelle est sa contenance en hectolitres ? Le niveau actuel de l’eau s’élève au 2/3 de la hauteur totale de la citerne
, quelle est la valeur de ce
contenu à raison de 1,15 € le litre ? 3 ) Un
terrassier creuse une fosse cubique de Sachant qu’on donne au terrassier 350 € par mètre cube creusé et 250 € par voyage , à combien revient ce travail. ? 4 ) On
a ficelé en croix une boite de forme cubique avec une ficelle de a)
Quelle est la longueur de l’arête de cette
boîte ? b)
On arrange dans cette boite des petits cubes de
|
|
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|