Pré requis:
Savoir utiliser le tableau de conversion des unité s de surface.
Le cube comme unité de mesure
Le tableau de conversion
ENVIRONNEMENT du dossier:
Index : vers l’accueil « warmaths »		Présentation 1°)Le tableau de conversion des capacités 2°) Les unités de volumes.			Présentation : tout sur les volumes		Info +++++ : ► Cours niveau VI et V ► travaux interdisciplinaires
DOSSIER : LES TABLEAUX de CONVERSIONS de mesures de Volumes et de capacités
TEST	COURS		Devoir Contrôle	Devoir évaluation * N°2 : Devoir Fiche n° 184. Exo :Série 1 Exo : série 2		Interdisciplinarité : FCHES …… Le volume			Corrigé Contrôle	Corrigé évaluation
COURS LES UNITES DE VOLUMES et de Capacités SYSTEME METRIQUE : Le « mètre cube » (noté : m^3 ) . ses Multiples et sous-multiples.

CUBE :
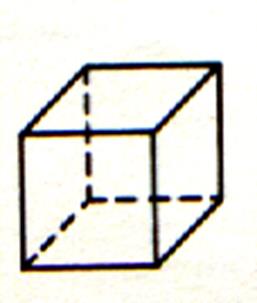
On appelle « cube » un volume ayant la forme d’un dé à jouer , c’est à dire terminé par six faces carrées égales entre elles ; tous les côtés du cube ont donc la même longueur.

Unités de volume :

On prend pour unités de volume les cubes construits sur les différentes unités de longueur. L’unité fondamentales est le mètre cube ou cube construit sur le mètre qu’on désignait par le signe m.c. est que l’on désigne maintenant par m³ .(m.c.= m³)

Ses multiples et sous multiples sont :

Myriamètre cube ( Mm.c. = M m³) ; kilomètre cube (Km.c.= K m³) ; hectomètre cube (Hm.c.= H m³) ;Décamètre cube(Dm.c.=Da m³) ; mètre cube (m.c.= m³) ; décimètre cube (dm.c.=d m³) ; centimètre cube (cm.c.= c m³) ; millimètre cube(mm.c.= m m³)

Comme dans les « aires » , nous avons des unités de différents ordres , et il est facile de faire voir qu’une unité d’un ordre quelconque vaut 1000 unités de l’ordre immédiatement inférieur .

Montrons , par exemple , que le mètre cube vaut 1000 décimètres cubes .

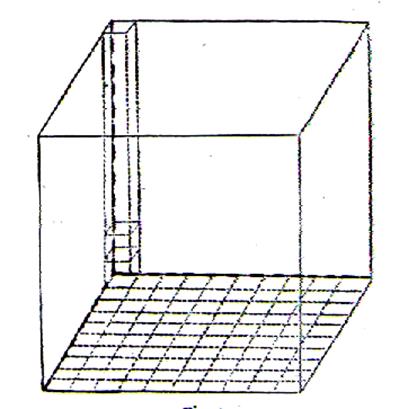
Prenons un carré de 1mètre de côté ; nous savons qu’il contient 100 décimètres carrés. Plaçons sur chacun d’eux un cube de un décimètre cube.

Nous formons ainsi une tranche ayant 1 mètre carré de base et 1 décimètre de hauteur et comprenant 100 décimètres cubes. En superposant dix tranches semblables , nous obtenons un cube ayant 1 mètre carré de base et 1 mètre de hauteur ; ce sera donc le mètre cube . Or , il se compose de dix tranches contenant chacune 100 décimètres cubes ; il contient donc 1000 décimètres cubes.

Nous pouvons donc regarder les différentes unités de volume comme formant deux séries , à partir de l’unité fondamentale ou mètre cube : l’une ascendante et comprenant des unités de mille en mille fois plus fortes , l’autre descendante et comprenant des unités de mille en mille fois plus faible.

MESURER UN VOLUME.

Mesurer un volume , c’est rechercher combien il contient d’unités de chaque ordre. Puisqu’il peut y avoir jusqu’à 999 unités de chaque ordre , le volume sera représenté par un nombre entier ou décimal , en ayant soit d’affecter 3chiffres à chaque ordre d’unités. Supposons , par exemple , qu’on ait trouvé qu’un volume contient 93 décamètres cubes 673 mètres cubes 36 décimètres cubes. Si nous prenons le mètre cube pour unité principale , le volume sera représenté par le nombre décimal 93673,036 m^{3 .}. D’ailleurs nous changerons facilement d’unité en multipliant ou divisant par 1000 , selon que nous prendrons une unité mille fois plus petite ou mille fois plus grande.

Supposons qu’un volume soit exprimé par le nombre 5075,3632 m³ , en prenant le mètre cube pour unité principale. On pourra dire que le volume contient : 5075 mètres cubes 3632 dix- millièmes. Si l’on veut énoncer les nombres des unités des différents ordres que contient le volume , on dira : 5 décamètres cubes 75 mètres cubes 363 décimètres cubes et 200 centimètres cubes. Si l’on prenait le centimètre cube comme unité principale ,le volume serait exprimé par le nombre :5075363200 cm³

Pour évaluer le volume d’une chose (tas de sable, meule de paille, contenance d’un bassin, d’un gazomètre...) on le compare au volume de cubes qui auraient pour arête une unité de longueur m, dm, cm, mm. On appelle ces cubes, selon leur arête, mètre cube (m^3), « Décimètre cube » (dm^3), « centimètre cube » (cm^3), « millimètre cube » (mm^3). On n’utilise pas d’unités multiples du mètre cube. Une unité cube vaut i 000 unités cubes immédiatement inférieures.

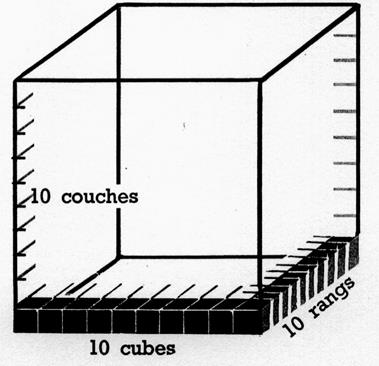
on peut voir, selon la figure, que le fond du cube porte 10 ´ 10 = 100 cubes de l’ordre immédiatement inférieur et que le cube enferme 10 couches semblables dans sa hauteur soit 100 ´ 10 = 1 000 cubes ayant pour arête l’unité de longueur immédiatement inférieure à celle qui est l’arête du cube observé.

On retiendra : 1 m^3 = 1000 d m^3 ; 1 dm^3= 1000 cm^3; 1 cm^3= 1000 m m^3 ( @ info + sur le tableau ) Exemple : Les différentes unités se lisent et s’écrivent par tranches de 3 chiffres : 8,543 267 950 m^3, c’est égal à : 8 m^3+ 543 dm^3+267 cm^3+950 mm^3

voir l’usage du tableau ci dessous :

Multiples du m^3

unité

Sous multiples du m^3

Il faut 3 chiffres par colonnes principales.

km^3

hm^3

dam^3

m^3

dm^3

cm^3

mm^3

8

5

4

3

2

6

7

9

5

0

Le tableau des unités de volumes utilise la numération en "base 1000" Alors que pour la surface on compte en "base 100" et la longueur on compte en "base 10" LES TABLEAUX DE CONVERSION DE VOLUME ET DE CAPACITE (voir le tableau) Sur le tableau des volumes on a superposé le tableau des "capacités"; pour cela on a superposé à partir de la correspondance : A savoir : 1 litre est égal à 1 dm^3d'eau à 4° centigrades On place le « l » et l ' on a réparti d'un coté (à gauche ) les multiples , de l ' autre ( à droite )les sous multiples.

km^3

hm^3

dam^3

m^3

dm^3

cm^3

mm^3

kl

hl

dal

l

dl

cl

ml

Autre tableau , plus détaillé , faisant apparaître la colonne réservée à la virgule.

km^3

hm^3

dam^3

m^3

dm^3

cm^3

mm^3

III ) Procédure permettant de transformer l ' unité de volume en multiples ou sous multiples à partir d'une grandeur donnée.

Exemple de conversion 32,24 dam³= ? ……..dm³

Pour remplir le tableau en vue de faire une conversion il faut suivre l'ordre suivant:

1°) placer la virgule du nombre donné sur le trait vertical "droit" de l'unité donnée.(da m³ , )

km^3

hm^3

dam^3

,

m^3

dm^3

cm^3

mm^3

2°) placer les chiffres du nombre dans en respectant l ' ordre donné :

km^3	hm^3		dam^3			,	m^3			dm^3			cm^3		mm^3
		0	0	3	2		2	4	0	0	0	0	0	0

la "grandeur" est placée dans le tableau ,la conversion peut se faire simplement:

3°) déplacer le virgule ; la mettre sur le trait vertical "droit" de l' unité "demandée " (d m³ , )

km^3	hm^3		dam^3			m^3			dm^3			,	cm^3		mm^3
		0	0	3	2	2	4	0	0	0	0		0	0

4° ) reporter le résultat , (lu sur le tableau )

0 32 240 000 , 0 soit 32 240 000 dm³

remarque : la virgule est dite flottante ;elle se trouve toujours sur le trait vertical "limite droite" de l 'unité concernée

Activités :

Placer dans le tableau ci -dessous les volumes suivants :

km^3

hm^3

dam^3

m^3

dm^3

cm^3

mm^3

1 765 , 798 m³ ; 5,3 m³ ; 78 507 dm³ ; 2854 cm³ ; 5 832 mm³

Solutions :

km^3	hm^3	dam^3		m^3			, ,	dm^3			,	cm^3			,	mm^3			,
			1	7	6	5		7	9	8
					5	3
					7	8		5	0	7
										2		8	5	4
														5		8	3	2

Autres exemples de conversions :

Activités : Convertir :

1 765 , 798 m³ en ………………………………dm³

; 5,3 m³ = ………………………..dm³

78 507 dm³ = ……………………m ³

2854 cm³ = ……………………m³

5 832 mm³ = …………………….cm³

Solutions : on reprend le tableau ci - dessus :

On complète de zéro ; on retire la virgule ; la déplacer dans la colonne de droite de l'unité demandée.

km^3	hm^3	dam^3			m^3			,,	dm^3			,,	cm^3			,	mm^3
		0	0	1	7	6	5		7	9	8		0	0	0		0	0	0
				0	0	5	3		0	0	0		0	0	0		0	0	0
					0	7	8		5	0	7		0	0	0		0	0	0
					0	0	0		0	0	2		8	5	4		0	0	0
						0	0		0	0	0		0	0	5		8	3	2

On relève dans le tableau :

1 765 , 798 m³ = 1 765 798 dm³ ;

5,3 m³ = 53 000 dm³

78 507 dm³ = 78, 507 m ³

2854 cm³ = 0, 002 854 m³

5 832 mm³ = 5 , 832 cm³

Suite : Convertir successivement : ( il suffit pour trouver les conversions successives de déplacer la virgule et de relever le résultat .

1 765 , 798 m³ en ………………………………dm³

1 765 , 798 m³ en ………………………………dam³

; 5,3 m³ = ………………………..dm³ = ……………………cm³ ;

78 507 dm³ = ……………………m ³ = ……………………cm³;

2854 cm³ =………………m³ =……………….dm³ = …………….mm³.;

5 832 mm³ = …………………….cm³ =…………………………….dm³

Relation entre les unités de volumes et les puissances de dix .

Applications au système métrique :
Unités de volume	Symboles	Valeur en mètre	Puissances de 10
Kilomètre cube	km	(1 000 m)	1 km = (1 10) m = (1 10) m = (1 10) m valeur décimale = 1 000 000 000 m = 10 ^9 m
Hectomètre cube	hm	(100 m)	1 hm = (1 10 ) m= 10 ^6 m
Décamètre cube	dam	(10) m	1 dam=(1 10 )m= 10 ^3 m
Mètre cube	m	(1 m)	1 m= (1 10 ) m= 1
Décimètre cube	dm	(0,1 m )	1dm= (1 10 ) m = 10 ^-3 m( = 0,001 m)
Centimètre cube	cm	(0,01 m )	1 cm = (1 10 ) m = 10 ^-6 m( = 0,000 001 m)
Millimètre cube	mm	(0, 001 m)	1 mm =( 1 10 ) m = 10 ^-9 m
Micron cube	(mu)m	(0 , 000 001 m)	1 mu = (1 10 ) m = 10 ^-18m

CONTROLE :

I ) Quelles sont les unités principales de mesure de volumes et de capacité?

II) A quel volume correspond un litre ?

III) Construire le tableau de conversion des unités de volumes et de capacité .

EVALUATION

Convertir dans l ' unité demandée:

270 dl

=