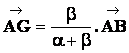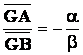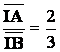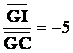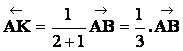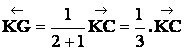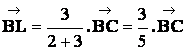Barycentre et lieu géométrique

	En cours de rédaction.




	On introduit ici un nouvel outil, particulièrement performant : le barycentre d'un système de points pondérés du plan ou de l'espace. Outre sa puissance pour résoudre des problèmes de mathématiques, le barycentre a de nombreuses applications, par exemple dans le domaine des statistiques (notion de moyenne pondérée) ou en physique. D'ailleurs, quand s'est posée la question de savoir si le calcul vectoriel pouvait s'étendre à l'espace, ce sont des physiciens comme Gibbs ou Heaviside qui ont apporté une partie des réponses.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité :

Voir exemple « concret » d’application

Corrigé Contrôle

Corrigé évaluation

COURS

Le barycentre est un point (dans le plan ou dans l'espace) que l'on détermine grâce à d'autres points connus. Ces points peuvent être pondérés, ce qui veut dire qu'ils sont affectés d'une valeur qui est prise en compte dans la détermination du barycentre. Le barycentre a plusieurs applications, comme notamment la recherche du centre de gravité d'un solide.
Le barycentre est un point mathématique (géométrie analytique) construit à partir d'un ensemble d'autres. Il correspond en statistiques à la notion de moyenne (ou espérance), en physique (cinématique, mécanique du point) à la notion de centre d'inertie (ou centre de masse) ou de centre de gravité, et en mécanique du solide à la notion de moment (moment d'inertie, moment cinétique), en analyse spatiale au point (Graphie) moyen ou point central
COURS : Barycentre de deux points. G barycentre de {(A , α) (B , β)} existe si et seulement si : α + β ≠ 0 Pour placer le barycentre G de {(A , α) (B , β)} , on utilise la formule : Par propriété d’homogénéité du barycentre, pour tout réel k non nul, si G est barycentre de {(A , α) (B , β)} , alors G est barycentre de {(A , kα) (B , kβ)} . La réciproque de la propriété d’associativité permet de remplacer un point pondéré d’un système par les points dont il est lui-même barycentre. Cette propriété s’applique notamment pour remplacer (A , k) par {(A ,a) (A , b)} avec a + b = k et k ≠ 0 . G isobarycentre des points A , B et C signifie que : G barycentre de {(A , k) (B , k) (C , k)} , avec k ≠ 0 L’isobarycentre de deux points est le milieu du segment formé par ces deux points. Le barycentre de deux points appartient à la droite formée par ces deux points.
Pour construire le barycentre de trois points, il est pratique de recourir à un barycentre partiel. De cette manière, placer un barycentre de trois points revient à placer deux barycentres de deux points. Pour déterminer le barycentre partiel à utiliser, il est recommandé de sélectionner un couple de points faisant apparaître un isobarycentre (en veillant à ce que la somme des coefficients soit non nulle, pour que le barycentre partiel existe).
Cours (Suite 1) :
On donne des points fixes « A , B , C , D,.. » et des nombres algébriques : ; ; ; ;…. On écrit l’opération + + + +… qui combine la multiplication d’un vecteur par un scalaire avec la somme géométrique , Si en particulier , dans le cas où : « + + + + …0 » Il existe un point « G » unique tel que : ( + + + + …) = + + + +… ( 1 ) et que l’on appelle « barycentre » des points « A,B,C,D,… »affectés des coefficients ; ; ; ;…. Le point « O » est un point arbitraire et en prenant « G » en « O » la relation (1) s’écrit aussi : + + + + …..= En particulier , si l’on a : + = et « + 0 » le point « G » est le point du segment « AB » tel que : On pourra alors , en opérant de proche en proche, déterminer « G » tel que : + + = et « + + 0 »
Problème 1 : Déterminer le point « G » tel que : + + = et avec = 3 ; = -2 ; = 5 . ; « A » , « B » , « C » sont donnés.
Solution : + = Prenons un point « I » quelconque de « AB » et écrivons : = 3 ( + ) - 2 ( + ) = 3 - 2 + 3 - 2 = + 3 - 2 Choisissons le point « I » tel que + 3 - 2 = ; c’est le point qui divise « AB » en segments soustractifs tels que : La condition de l’énoncé : + = s’écrit + = Ce qui montre que « G » est sur la droite « CI » et tel que :
Problème 2 : Déterminer le point « G » tel que : + + = et avec = 5 ; = 7 ; = - 7 . ; « A » , « B » , « C » sont donnés.
Solution : indication Suivre la méthode du « Pb1 » en déterminant sur « BC » le point « I » tel que : 5 + 3 =

Problème 3 : Traiter le cas général de la détermination de « G » tel que : + + = ; « A » , « B » , « C » sont donnés et « + + 0 » Nota : on pourra généraliser pour quatre points « ABCD » ou cinq point « ABCDE ».
Cours (suite 2 )
			Info sur le calcul de l’aire d’un triangle quelconque .
Parmi les théorème de géométrie élémentaire , il est souvent utile de considérer celui qui donne le carré d’un côté en fonction des deux autres côtés et de la projection de l’un de ces côtés sur l’autre.

Quel que soit le cas de figure , on a : = + Ce théorème se traduit dans le cours par la relation : « a ² = b ² + c ² – 2 b c cos A. »
Ce théorème permet, étant donné des points fixes « ABCD.. »de déterminer le lieu des points « M » tels que : + + + + … = k ; ; ; ; ;… étant des coefficients algébriques et « k » une constante , donnés. « k » est de signe quelconque , mais doit être homogène au carré d’une longueur ( homogénéité)

Problème 4 :
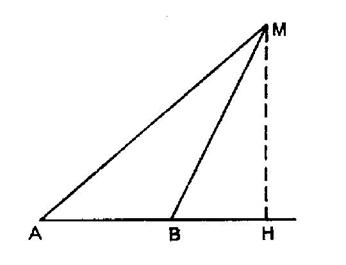
« A » et « B » étant deux points fixes donnés , lieu des points « M » tels que : 3 + 2 = m ² ; « m » étant une longueur donnée.
Solution : « G » étant un point quelconque de « AB » , d’après le théorème rappelé au « cours suite 2 »
		= + - 2 . = + - 2 .
« H » étant la projection de « M » sur « AB ». On en déduit : 3 + 2 = 5 + 3 + 2 - 2 ( 3 + 2 ) On détermine « G » ( Barycentre de « A » et « B » de coefficients « 3 » et « 2 » ) par la condition : 3 + 2 = 0 et le point « M » doit satisfaire à : 5 = m ²- 3 - 2 . Tous les termes du second membre sont connus et , si ce second membre est positif, on a : = constante. Le milieu de « M » dans le plan est le cercle de centre « G » et de rayon : Dans l’espace , le lieu « M » serait une sphère de centre « G ».
Problème 5 :
Lieu des points « M » tels que : 7+ 3 = 5 a ² « A » et « B » étant fixes et « a » désignant la longueur « AB ». Calculer les longueurs « GA » et « GB » sachant que : et GA – GB = a (achever comme au problème 4 )
Problème 6 :
Lieu des points 3- = 4 a ² « a » étant la mesure du segment fixe « AB » .
Cours ( suite 3)
Il peut y avoir plusieurs points fixes. ON procédera de proche en proche comme ci-dessus. Mais il y aura lieu de voir si la somme des coefficients + + + + … est différente de zéro ou au contraire nulle.

Problème 7 :
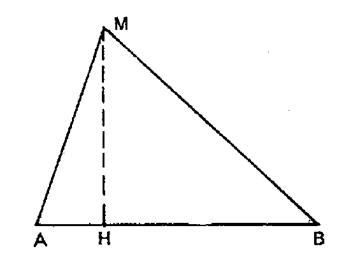
On donne trois points « ABC » non alignés. Lieu des points « M » tels que : + + = k ² , « k » est une longueur donnée.
Solution .
Soit « G₁ » , un point de « AB » ; « H » étant la projection de « M » sur « AB » , on écrit :
	= + - 2 . = + - 2 .
On en déduit par addition (membre à membre ) : + = 2 + +- 2 (+) En prenant le point « G » , au milieu de « AB » , (+) est nul et il reste : 2 + = k² - ( F ) On est ramené à un problème du type traité aux problèmes « 4 » et « 5 ». « G » étant un point de la droite G ₁ C et « K » la projection de « M » sur cette droite :
		= + - 2 . = + - 2 .
D’où : 2 + = 3 + 2 + - 2 ( 2 + ) Et en prenant « G » tel que « + 2 + = 0 » , c'est-à-dire « G » confondu avec le point de concours des médianes du triangle « ABC » et utilisant la relation « F » Il reste : 3 = k ² - 2 - et sous réserve que le second membre soit positif , le lieu du point « M » est un cercle ( dans le plan) ou une sphère ( dans l’espace) de centre « G »
Problème 8 :
On donne trois points « ABC » non alignés. Lieu des points « M » tels que : 2 + 3 - = 0
Vers la solution : procéder avec rigueur comme ci-dessus ( pb 7 ) en déterminant d’abord le point « G₁ » de « AB » tel que : 2 + 3 = 0 , puis le point « G » de CG₁ tel que 5 - = 0
Problème 9 :
On donne trois points « ABC » non alignés. Lieu des points « M » tels que : 5 + 7 + = k ² , « k » est une longueur donnée.
	Dans l’hypothèse où la somme des coefficients de , , etc ; est nulle, la solution se présente comme ce qui suit… ,

Problème 10 :
On donne trois points « ABC » non alignés. Lieu des points « M » tels que : + 2 - 3 = k ² , « k » est une longueur donnée.
Solution :
Soit « G » un point de « AB » ; « H » étant la projection de « M » sur « AB » , des calculs analogues à ceux des problèmes précédents donnent : de + 2 = 3 + + 2 - 2 ( + 2 ) Choisissons le point « G » tel que : + 2 = 0 La relation de l’énoncé s’écrit alors : 3 + + 2 - 3 = k ou - = ( k - - 2 ) Et nous apprend que le lieu du point « M » est , dans le plan , une droite , dans l’espace un plan ,perpendiculaire à « CG » en un point parfaitement déterminé. ( voir « médiane »)

Problème 11 :
On donne trois points « ABC » non alignés. Lieu des points « M » tels que : 5+ 3 - 8 = 0

Cours ( suite 4)
Signalons que les questions de cette nature se résolvent plus rapidement si l’on a préalablement étudié les propriétés du produit scalaire de deux vecteurs et établi à cette occasion la relation de « Leibniz » + + + + … = ( ++ + ….) + + + …………… « G » étant le point tel que : + + +……= et « + + +……0 » Signalons également que les lieux géométriques étudiés dans les problèmes ci-dessus apparaissent dans de multiples questions et notamment dans le cas de combinaisons diverses des puissances d’un point par rapport à deux cercles ou à deux sphères.

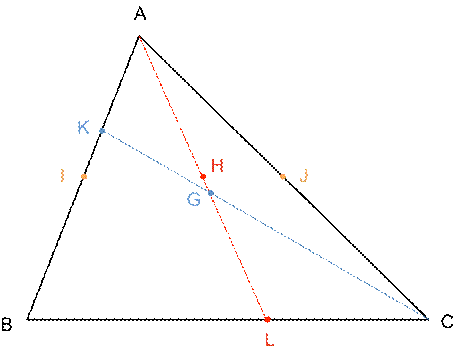
Problème 12: A , B et C sont trois points non alignés du plan. G est le barycentre des points pondérés (A , 8) (B , 4) et (C , 6) . H est le barycentre des points pondérés (A , 10) (B , 4) et (C , 6) . Le point I est le milieu du segment [AB] . Le point J est le milieu du segment [AC] . 1. Construire la figure. 2. Montrer que les points H, I et J sont alignés. 3. En déduire le point d’intersection des droites (IJ) et (AG) .
CORRIGE: Pour placer les barycentres G et H , on peut utiliser la propriété des barycentres partiels (également appelée propriété d’associativité) afin de faciliter la construction. • Placer le point G G est le barycentre des points pondérés (A , 8) (B , 4) et (C , 6) . On appelle K le barycentre des points pondérés (A , 8) et (B , 4) , qui existe car 8 + 4 ≠ 0 . Par associativité du barycentre, G est alors barycentre des points (K , 8 + 4) et (C , 6) . On peut donc placer le point K puis placer le point G . Placer le point K K barycentre des points (A , 8) (B , 4) ⇔ K barycentre des points (A , 2) (B , 1) , par homogénéité du barycentre. D’où : Placer le point G Finalement, G est barycentre des points (K , 12) (C , 6) , ou encore (K , 2) (C , 1) par homogénéité. D’où : • Placer le point H H est le barycentre des points pondérés (A , 10) (B , 4) et (C , 6) . On appelle L le barycentre des points pondérés (B , 4) et (C , 6) , qui existe car 4 + 6 ≠ 0 . Par associativité du barycentre, H est alors barycentre des points (A , 10) et (L , 4 + 6) . On peut donc placer le point L puis placer le point H . Placer le point L L barycentre des points (B , 4) (C , 6) ⇔ L barycentre des points (B , 2) (C , 3) , par homogénéité du barycentre. D’où : Placer le point H Finalement, H est barycentre des points (A , 10) (L , 10) : H est donc le milieu du segment [AL] . 2. Pour démontrer que les points H , I et J sont alignés, on peut montrer que H est barycentre des points I et J . On sait que H est barycentre des points (A , 10) (B , 4) (C , 6) . Pour tout couple de réels (a , b) tels que a + b ≠ 0 : aAA→ + bAA→ = 0→ Par réciproque de la propriété d’associativité du barycentre, on a donc : H barycentre des points (A , 6) (A , 4) (B , 4) (C , 6) , car A est barycentre des points (A , 6) (A , 4) . Or : • I milieu de [AB] ⇔ I barycentre des points (A , 4) (B , 4) • J milieu de [AC] ⇔ J barycentre des points (A , 6) (C , 6) Par associativité du barycentre, on en déduit que : H est le barycentre des points (I , 8) (J , 12) . Or le barycentre de deux points appartient à la droite formée par ces deux points. Le point H appartient donc à la droite (IJ) . Les points H;I ; J sont donc alignés. 3. On vient de montrer que le point H appartient à la droite (IJ) . Il semble que le point H appartienne également à la droite (AG) , ce que l’on va tenter de démontrer. On sait que H est le barycentre des points (A , 10) (B , 4) (C , 6) . Par réciproque de la propriété d’associativité du barycentre, on a donc, de la même manière que précédemment : H barycentre des points (A , 2) (A , 8) (B , 4) (C , 6) , car A est barycentre des points (A , 2) (A , 8) . Or, on sait que G est la barycentre des points (A , 8) (B , 4) (C , 6) . Par associativité du barycentre, on en déduit que : H est le barycentre des points (A , 2) (G , 18) . Or le barycentre de deux points appartient à la droite formée par ces deux points. Le point H appartient donc effectivement à la droite (AG) . Finalement, le point H appartient aux deux droites non parallèles (IJ) et (AG) . Le point “H” est donc le point d’intersection des droites ( I J ) et ( A G ) Le point H est donc le point d’intersection des droites (IJ) et (AG) .

TRAVAUX AUTO FORMATIFS.

CONTROLE


EVALUATION.
Refaire les problèmes……… ;;;;