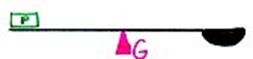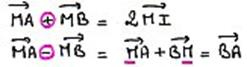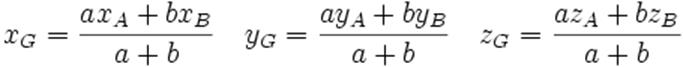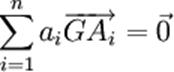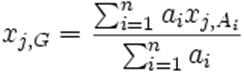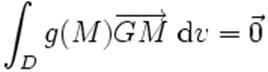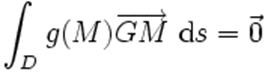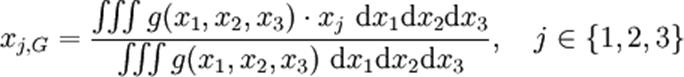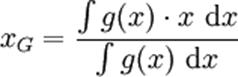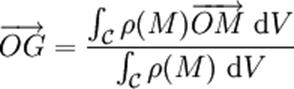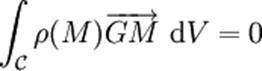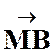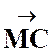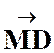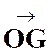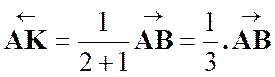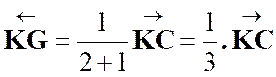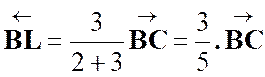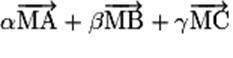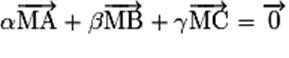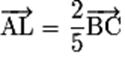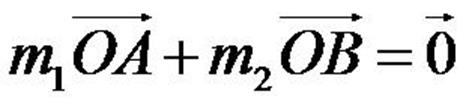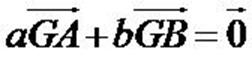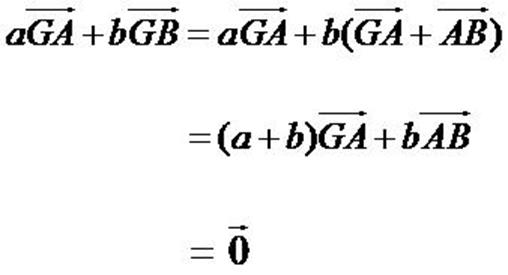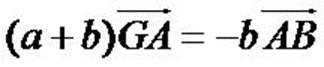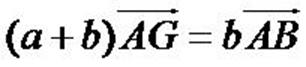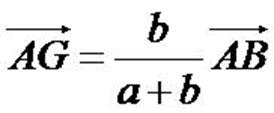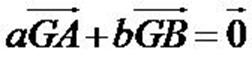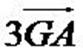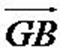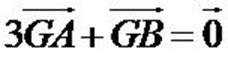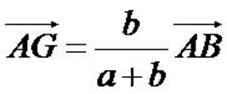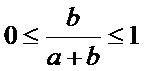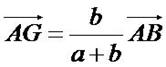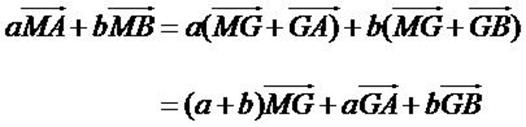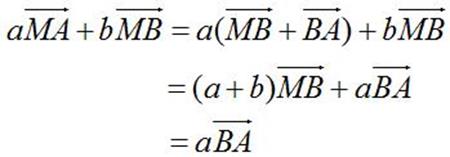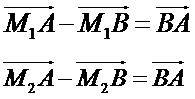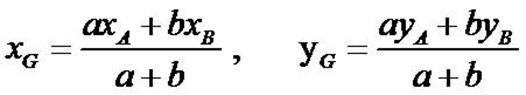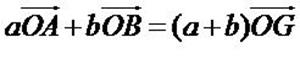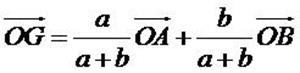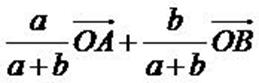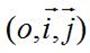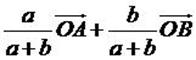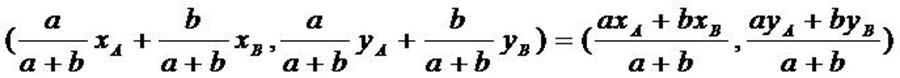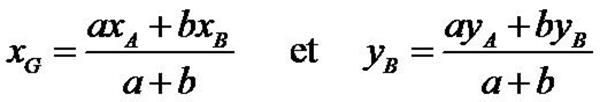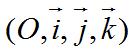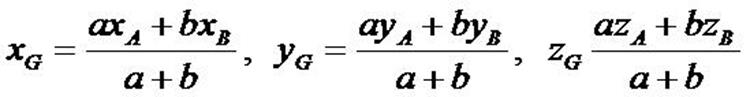|
|
Le barycentre
est un point (dans le plan ou dans l'espace) que l'on détermine grâce à
d'autres points connus. Ces points peuvent être pondérés, ce qui veut dire
qu'ils sont affectés d'une valeur qui est prise en compte dans la
détermination du barycentre. Le barycentre a plusieurs applications, comme
notamment la recherche du centre de gravité d'un solide.
|
|
|
|
Le chapitre des barycentres allie
géométrie vectorielle et calculs. Il y a peu de cours, par contre beaucoup de
méthodes sont à apprendre.
Qu'est ce
que c'est, et à quoi ca sert ?
Le barycentre est un point, un
endroit spécial. Si on parlait du barycentre d'un objet, ce serait le
"centre" de cet objet, c'est à dire le point d'équilibre de
l'objet. En physique, ce point sera utilisé pour étudier l'objet.
Pourquoi parle-t'on de points "pondérés"?
- Imaginez votre double décimètre. Si vous le posez à plat sur une pointe de
métal, vous devrez positionner la pointe de métal (G) au centre de la règle
pour qu'elle se tienne en équilibre : normal, votre double décimètre est
identique à chaque extrémité, chaque point est affecté du même poids, le
barycentre est alors l'"isobarycentre" ( iso
veut dire égal).
 -
Imaginez maintenant une louche: elle est bien plus lourde du coté bombé que
du coté du manche. Si vous la mettez sur une pointe
de métal (G), en positionnant la pointe au milieu de la longeur
de la louche, celle ci va pencher du coté le plus lourd. Pour compenser cela et trouver
l'équilibre, on va poser sur le manche un poids supplémentaire P. Le
centre de la louche sera alors le barycentre du coté bombé affecté du poids
"1" , et du manche affecté du poids P. -
Imaginez maintenant une louche: elle est bien plus lourde du coté bombé que
du coté du manche. Si vous la mettez sur une pointe
de métal (G), en positionnant la pointe au milieu de la longeur
de la louche, celle ci va pencher du coté le plus lourd. Pour compenser cela et trouver
l'équilibre, on va poser sur le manche un poids supplémentaire P. Le
centre de la louche sera alors le barycentre du coté bombé affecté du poids
"1" , et du manche affecté du poids P.
  -
Imaginez enfin que non, finalement, on ne met pas de poids sur le manche pour
compenser. Alors pour rétablir l'équilibre, il faudra trouver la position
de G la plus adaptée, et donc la rapprocher du coté lourd. -
Imaginez enfin que non, finalement, on ne met pas de poids sur le manche pour
compenser. Alors pour rétablir l'équilibre, il faudra trouver la position
de G la plus adaptée, et donc la rapprocher du coté lourd.

La
plupart des objets de notre vie sont asymétriques. Pour pouvoir étudier les
forces qui s'y exercent, leur mouvement ou tout
autre chose en physique, il faut "réduire" cet objet à un seul
point. C'est le barycentre qui sera choisi, et on l'appellera en physique, le
centre de gravité.
Ce qu'il faut savoir :
- la définition du barycentre,
- la propriété du barycentre,
- les petites propriétés,
- l'association de barycentre.
Ce qu"il
faut savoir faire:
- Construire le barycentre de 2 points, de 3 points,
- Montrer qu'un point est le barycentre de 2 ou 3 points,
- Montrer que 3 points sont alignés,
- Trouver des ensembles de points.
Rappels préliminaire nécessaires :
- La relation de Chasles: 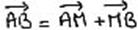
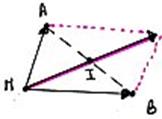
- La règle du parallélogramme, avec I le milieu de AB : 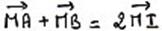
- A retenir pour les résolutions d'exercices :
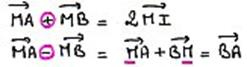 
Définition fondamentale : G est le Bar (A,a)
(B,b) alors 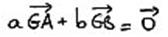
Construction d'un barycentre :
 Sans les coordonnées : Sans les coordonnées :
De la définition, grace à la relation de Chasles, on obtient la formule
permettant de construire G connaissant A et B :

Certains profs admettent
l'utilisation directe de la formule, d'autres veulent que vous la retrouviez
à chaque fois. Regardez dans les exos corrigés comment votre prof procède et
faites de la même façon.
Pour retrouver ces formules:
Partez de la définition. Gardez GA puisque AG doit apparaitre
dans la formule finale, mais faites Chasles sur GB pour le faire
disparaître. Pointez sur le seul point qui reste, A. Vous obtenez aGA + b(GA + AB) = 0. Développez, transformez les GA en AG, isolez-le, et c'est fini.
Avec 3 points la formule devient :
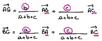
 Avec coordonnées : Avec coordonnées :

Formules à adapter avec 3 points.
Montrer qu'un point est le
barycentre de 2 points, ou 3 points:
Le but est donc d'utiliser les
données du problème pour arriver à une formule du meme
type que la définition du barycentre: 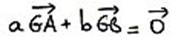
Exemple : AC = 3 CB, exprimer A comme le
bary de B et C:
On doit donc trouver un formule du genre aAB + bAC = 0.
On ne touche pas au vecteur AC, on rapatrie CB à gauche du =, et comme CB doit disparaitre,
on fait Chasles en pointant sur A:
AC -3 (CA+AB) =0 d'ou AC - 3CA - 3AB =0 d'ou 4AC - 3AB = 0. A est donc le
Bary de (B,-3) (C,4).
Dans l'article suivant, nous
étudierons les méthodes concernant les barycentres partiels ( ou barycentres associés ) ainsi que les exercices
types pour trouver des ensembles de points.
|
|
|
|
Info Internet :
|
|
|
|
Le barycentre est un point mathématique (géométrie
analytique) construit à partir d'un ensemble d'autres. Il correspond
·
en
statistiques à la notion de moyenne (ou espérance),
·
en
physique (cinématique, mécanique du point) à la notion de centre d'inertie (L'inertie d'un corps découle de la
nécessité d'exercer une force sur celui-ci pour modifier sa vitesse
(vectorielle). Ainsi, un corps immobile ou en mouvement rectiligne uniforme
(se...) (ou centre de masse (La masse est une propriété fondamentale de la matière qui se
manifeste à la fois par l'inertie des corps et leur interaction
gravitationnelle.)) ou de centre de gravité (La gravitation est une des quatre
interactions fondamentales de la physique.),
·
et en
mécanique (Dans le langage courant,
la mécanique est le domaine des machines, moteurs, véhicules, organes
(engrenages, poulies, courroies, vilebrequins, arbres de transmission,
pistons, ...), bref, de tout ce qui produit ou transmet un...) du
solide à la notion de moment (moment d'inertie, moment cinétique),
·
en
analyse spatiale au point (Graphie)
moyen ou point central
|
|
|
|
En physique (La physique (du grec φυσικη) est
étymologiquement la science de la nature. Son champ d'application actuel est
néanmoins plus restreint : la physique...)
Le barycentre (Le
barycentre est un point mathématique (géométrie analytique) construit à
partir d'un ensemble d'autres. Il correspond) de barus (poids) et centre est initialement le
centre des poids (Le poids d'un corps nu ou force de
pesanteur est la force exercée sur un corps (de masse m) immobile dans le
référentiel terrestre (c’est-à-dire, lié à l'objet solide Terre en rotation),
par...). C'est donc une notion physique et mécanique. Le
premier à avoir étudié le barycentre en tant que centre des poids (ce qu'on
appelle de nos jours (Le jour ou la journée est l'intervalle
qui sépare le lever du coucher du Soleil ; c'est la période entre deux
nuits, pendant laquelle les rayons du Soleil éclairent le ciel. Son...)
le centre de gravité) est le mathématicien et physicien Archimède. Il est un
des premiers à comprendre et expliciter le principe des moments, le principe
des leviers et le principe du barycentre. Il écrit dans son traité Sur le
centre de gravité de surface plane (La plane
est un outil pour le travail du bois. Elle est composée d'une lame semblable
à celle d'un couteau, munie de deux poignées, à chaque extrémité de la lame.
Elle permet le dégrossissage et le creusage de formes courbes, galbées et
même...):
" Tout corps pesant a un
centre de gravité bien défini en lequel tout le poids du corps peut être
considéré comme concentré. "
Son principe des moments et des
leviers lui permet de construire assez simplement le barycentre O de
deux points de masses m1 et
m2 différentes.

Pour que la balance soit en
équilibre, il faut que les moments 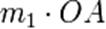 et et
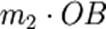 soient égaux. Si par exemple la masse m1 est 4 fois plus importante que
la masse m2, il faudra que
la longueur (La longueur
d’un objet représente la distance entre deux de ses extrémités, les plus
éloignées possibles. Lorsque l’objet est filiforme ou en forme de lacet, sa
longueur est souvent celle de...) OA soit 4 fois
plus petite que la longueur OB. Cette condition se traduit de nos
jours par l'égalité vectorielle soient égaux. Si par exemple la masse m1 est 4 fois plus importante que
la masse m2, il faudra que
la longueur (La longueur
d’un objet représente la distance entre deux de ses extrémités, les plus
éloignées possibles. Lorsque l’objet est filiforme ou en forme de lacet, sa
longueur est souvent celle de...) OA soit 4 fois
plus petite que la longueur OB. Cette condition se traduit de nos
jours par l'égalité vectorielle
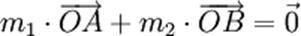
C'est le premier à avoir cherché
des centres de gravité de surface comme des demi disques,
des paraboles. Il procède par approximations successives et a pu prouver que
la recherche (La recherche scientifique désigne en
premier lieu l’ensemble des actions entreprises en vue de produire et de
développer les connaissances scientifiques. Par extension métonymique, la
recherche scientifique...) d'un centre de gravité
utilise des méthodes analogues à celle du calcul d'aire. Son travail est
prolongé par celui de Paul Guldin (1635/1640) dans
son traité Centrobaryca et celui de Leibniz
à qui l'on doit la fonction vectorielle de Leibniz.
La notion de centre d'inertie G
pour un système non solide est une notion dégagée par Christiaan Huygens
(1654), lors de l'établissement de sa théorie (Le mot théorie vient du mot grec theorein, qui signifie
« contempler, observer, examiner ». Dans le langage courant, une
théorie est une idée ou une connaissance spéculative, souvent basée sur
l’observation ou l’expérience,...) des
chocs : même s'il sait que P = P0, il n'est pas évident pour
lui que G ira à vitesse (La vitesse est une grandeur physique qui permet d'évaluer
l'évolution d'une quantité en fonction du temps.)
constante. En particulier au moment de la percussion, où des forces
quasi-infinies entrent en jeu, avec éventuellement bris de la cible, G n'en
continue pas moins imperturbé son mouvement :
cela paraît mirifique à Huygens, qui ne connaît pas encore le calcul différentiel (Un différentiel est un système mécanique
qui a pour fonction de distribuer une vitesse de rotation de façon adaptative
aux besoins d'un ensemble mécanique.). C'est alors qu'il
énonce le principe de mécanique :
" Le barycentre d'un
système matériel se meut comme si toute la masse du système y était
transportée, les forces extérieures du système agissant toutes sur ce
barycentre. "
On peut remarquer le glissement
subtil entre barycentre, centre des poids (= centre de gravité) comme le
voyait Archimède et barycentre, centre des masses (= centre d'inertie).
Autres champs d'application
Le barycentre, créé dans le cadre
de la physique et de la mécanique, s'est vite révélé très utile dans bien
d'autres domaines.
En géométrie (Selon
la définition donnée par Euclide dans ses Éléments, la géométrie serait la
science mathématique des figures dans le plan et des volumes (les corps, au
sens classique) dans l’espace. Cette acceptation, valable durant
l'Antiquité...), il permet de repérer des points par rapport à
d'autres points : ce sont les coordonnées barycentriques. C'est l'outil (Un outil est un objet finalisé utilisé
par un être vivant dans le but d'augmenter son efficacité naturelle dans
l'action. Cette augmentation se traduit par la simplification des actions
entreprises, par une plus...) privilégié pour démontrer
des alignements et des concours. On peut dire que la géométrie
vectorielle (Cet article traite des
opérations portant sur les vecteurs en géométrie euclidienne.)
est la géométrie des vecteurs et des combinaisons linéaires alors que la géométrie
affine (La géométrie affine est la
géométrie des espaces affines : il s'agit grossièrement d'ensembles de
points définis par des propriétés spécifiques permettant de parler
d'alignement, de parallélisme,...) est celle des points
et des barycentres.
En statistique (La
statistique (par opposition à une statistique) est l'ensemble des instruments
et de recherches mathématiques permettant de déterminer les caractéristiques
d'un ensemble de données (généralement vaste). Les statistiques (au pluriel)
sont le...), il permet le calcul et la représentation des
moyennes pondérées. En probabilité (Probabilité vient du latin probare (prouver, ou tester).
Le mot probable signifie « qui peut se produire » dans le cas de
futures éventualités, ou « certainement vrai »,...),
on le retrouve dans l'espérance mathématique (L'espérance mathématique est une valeur
numérique permettant de mesurer le degré d'équité d'un jeu de hasard. Elle
est égale à la somme des gains (et des pertes) pondérés par la...).
En logistique (La logistique est une activité de services qui a pour
objet de gérer les flux de matières en mettant à disposition et en gérant des
ressources correspondant aux besoins, aux...),
c'est un outil puissant de décision.
En chimie (La chimie est la science qui étudie la composition et les
réactions de la matière.), il permet de calculer
la polarité d'une molécule.
|
|
|
|
|
|
|
|

e
barycentre
est un point mathématique (géométrie analytique) construit à partir d'un
ensemble d'autres. Il correspond
·
en statistiques à la notion de moyenne (ou
espérance),
·
en physique (cinématique, mécanique du point) à la
notion de centre d'inertie (L'inertie d'un corps découle de la nécessité
d'exercer une force sur celui-ci pour modifier sa vitesse (vectorielle).
Ainsi, un corps immobile ou en mouvement rectiligne uniforme (se...)
(ou centre de masse (La masse est une propriété fondamentale de la
matière qui se manifeste à la fois par l'inertie des corps et leur
interaction gravitationnelle.)) ou de centre de gravité (La
gravitation est une des quatre interactions fondamentales de la physique.),
·
et en mécanique (Dans le langage courant, la mécanique est le domaine des machines,
moteurs, véhicules, organes (engrenages, poulies, courroies, vilebrequins,
arbres de transmission, pistons, ...), bref, de tout ce qui produit ou
transmet un...) du solide à la notion de moment (moment
d'inertie, moment cinétique),
·
en analyse spatiale au point (Graphie) moyen ou point central.
On
utilise également ce concept pour la construction de courbes de Bézier.
Un peu d'histoire
En
physique (La physique
(du grec φυσικη) est étymologiquement la
science de la nature. Son champ d'application actuel est néanmoins plus
restreint : la physique...)
Le
barycentre (Le barycentre est un point mathématique (géométrie
analytique) construit à partir d'un ensemble d'autres. Il correspond)
de barus (poids) et centre est
initialement le centre des poids (Le poids d'un corps nu ou force de pesanteur est la
force exercée sur un corps (de masse m) immobile dans le référentiel
terrestre (c’est-à-dire, lié à l'objet solide Terre en rotation), par...).
C'est donc une notion physique et mécanique. Le premier à avoir étudié le
barycentre en tant que centre des poids (ce qu'on appelle de nos jours (Le jour ou la journée est l'intervalle qui sépare
le lever du coucher du Soleil ; c'est la période entre deux nuits,
pendant laquelle les rayons du Soleil éclairent le ciel. Son...)
le centre de gravité) est le mathématicien et physicien Archimède. Il est un
des premiers à comprendre et expliciter le principe des moments, le principe des
leviers et le principe du barycentre. Il écrit dans son traité Sur le
centre de gravité de surface plane (La plane est un outil pour le travail du bois. Elle est
composée d'une lame semblable à celle d'un couteau, munie de deux poignées, à
chaque extrémité de la lame. Elle permet le dégrossissage et le creusage de
formes courbes, galbées et même...):
" Tout
corps pesant a un centre de gravité bien défini en lequel tout le poids du
corps peut être considéré comme concentré. "
Son
principe des moments et des leviers lui permet de construire assez simplement
le barycentre O de deux points de masses m1
et m2 différentes.

Pour
que la balance soit en équilibre, il faut que les moments 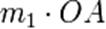 et et
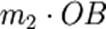 soient
égaux. Si par exemple la masse m1
est 4 fois plus importante que la masse m2,
il faudra que la longueur (La longueur d’un objet représente la distance entre deux de ses
extrémités, les plus éloignées possibles. Lorsque l’objet est filiforme ou en
forme de lacet, sa longueur est souvent celle de...) OA
soit 4 fois plus petite que la longueur OB. Cette condition se traduit
de nos jours par l'égalité vectorielle soient
égaux. Si par exemple la masse m1
est 4 fois plus importante que la masse m2,
il faudra que la longueur (La longueur d’un objet représente la distance entre deux de ses
extrémités, les plus éloignées possibles. Lorsque l’objet est filiforme ou en
forme de lacet, sa longueur est souvent celle de...) OA
soit 4 fois plus petite que la longueur OB. Cette condition se traduit
de nos jours par l'égalité vectorielle
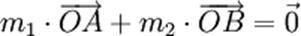
C'est
le premier à avoir cherché des centres de gravité de surface comme des
demi-disques, des paraboles. Il procède par approximations successives et a
pu prouver que la recherche (La recherche scientifique désigne en premier lieu l’ensemble des
actions entreprises en vue de produire et de développer les connaissances
scientifiques. Par extension métonymique, la recherche scientifique...)
d'un centre de gravité utilise des méthodes analogues à celle du calcul
d'aire. Son travail est prolongé par celui de Paul Guldin
(1635/1640) dans son traité Centrobaryca et
celui de Leibniz à qui l'on doit la fonction vectorielle de Leibniz.
La
notion de centre d'inertie G pour un système non solide est une notion
dégagée par Christiaan Huygens (1654), lors de l'établissement de sa théorie (Le mot théorie vient du mot grec theorein, qui signifie
« contempler, observer, examiner ». Dans le langage courant, une
théorie est une idée ou une connaissance spéculative, souvent basée sur
l’observation ou l’expérience,...) des chocs : même
s'il sait que P = P0, il n'est pas évident pour lui que G ira à vitesse (La vitesse est une grandeur physique qui permet d'évaluer l'évolution
d'une quantité en fonction du temps.) constante. En
particulier au moment de la percussion, où des forces quasi-infinies entrent en
jeu, avec éventuellement bris de la cible, G n'en continue pas moins imperturbé son mouvement : cela paraît mirifique
à Huygens, qui ne connaît pas encore le calcul différentiel
(Un différentiel est un système mécanique qui a pour fonction de distribuer
une vitesse de rotation de façon adaptative aux besoins d'un ensemble
mécanique.). C'est alors qu'il énonce le principe de
mécanique :
" Le
barycentre d'un système matériel se meut comme si toute la masse du système y
était transportée, les forces extérieures du système agissant toutes sur ce
barycentre. "
On
peut remarquer le glissement subtil entre barycentre, centre des poids (=
centre de gravité) comme le voyait Archimède et barycentre, centre des masses
(= centre d'inertie).
Autres champs d'application
Le
barycentre, créé dans le cadre de la physique et de la mécanique, s'est vite
révélé très utile dans bien d'autres domaines.
En
géométrie (Selon la définition donnée par Euclide dans ses
Éléments, la géométrie serait la science mathématique des figures dans le
plan et des volumes (les corps, au sens classique) dans l’espace. Cette
acceptation, valable durant l'Antiquité...), il permet de
repérer des points par rapport à d'autres points : ce sont les
coordonnées barycentriques. C'est l'outil (Un outil est un objet finalisé utilisé par un être vivant dans le but
d'augmenter son efficacité naturelle dans l'action. Cette augmentation se
traduit par la simplification des actions entreprises, par une plus...)
privilégié pour démontrer des alignements et des concours. On peut dire que
la géométrie vectorielle
(Cet article traite des opérations portant sur les vecteurs en géométrie
euclidienne.) est la géométrie des vecteurs et des
combinaisons linéaires alors que la géométrie affine
(La géométrie affine est la géométrie des espaces affines : il s'agit
grossièrement d'ensembles de points définis par des propriétés spécifiques
permettant de parler d'alignement, de parallélisme,...)
est celle des points et des barycentres.
En
statistique (La statistique (par opposition à une statistique)
est l'ensemble des instruments et de recherches mathématiques permettant de
déterminer les caractéristiques d'un ensemble de données (généralement
vaste). Les statistiques (au pluriel) sont le...), il permet le
calcul et la représentation des moyennes pondérées. En probabilité
(Probabilité vient du latin probare (prouver, ou tester). Le mot probable
signifie « qui peut se produire » dans le cas de futures
éventualités, ou « certainement vrai »,...),
on le retrouve dans l'espérance mathématique
(L'espérance mathématique est une valeur numérique permettant de mesurer le degré
d'équité d'un jeu de hasard. Elle est égale à la somme des gains (et des
pertes) pondérés par la...).
En
logistique (La logistique est une activité de services qui a pour objet de gérer
les flux de matières en mettant à disposition et en gérant des ressources
correspondant aux besoins, aux...), c'est un outil
puissant de décision.
En
chimie (La chimie est la science qui étudie la composition et les réactions de
la matière.), il permet de calculer la polarité d'une
molécule.
Développement mathématique (Les
mathématiques désignent la science du vrai et du faux en général.
C'est-à-dire qu'elle ne s'attache pas à dire ce qui est vrai ou faux dans
l'absolu mais relativement à des...)
Les
mathématiques généralisent la construction d'Archimède du point d'équilibre
de deux points affectés de deux masses positives progressivement à des
ensembles plus complexes. Les coefficients peuvent être négatifs : Le
barycentre des points A et B affectés des masses a et b (a + b non nul) est
l'unique point G tel que
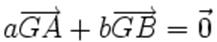 . .
Les
coordonnées de G sont alors
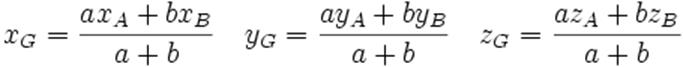
Le
nombre
(Un nombre est un concept caractérisant une unité, une collection d'unités ou
une fraction d'unité.) de points peut passer à
trois points, quatre points et se généraliser à n points. Si la somme
des masses ai est non
nulle, le barycentre du système 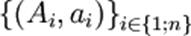 est
le point G tel que est
le point G tel que
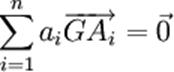 . .
Les
coordonnées sont données (Dans les technologies de l'information
(TI), une donnée est une description élémentaire, souvent codée, d'une chose,
d'une transaction d'affaire, d'un événement, etc.)
par les formules, pour j variant de 1 à la dimension (Dans le sens commun, la
notion de dimension renvoie à la taille ; les dimensions d'une pièce
sont sa longueur, sa largeur et sa profondeur/son épaisseur, ou bien son
diamètre si...) de l'espace
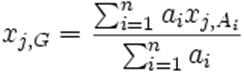
C'est
sous cette forme qu'il devient un outil puissant en géométrie affine
(En mathématiques, affine peut correspondre à :).
Le
nombre de points peut même devenir infini, permettant de trouver le
barycentre d'une courbe (En géométrie, le mot courbe, ou ligne
courbe désigne certains sous-ensembles du plan, de l'espace usuels. Par
exemple, les droites, les segments, les lignes polygonales et les cercles
sont des courbes.) ou d'une surface.
Si
l'ensemble (En théorie des ensembles, un ensemble, désigne intuitivement une
collection d’objets (que l'on appelle éléments de l'ensemble), « une
multitude qui peut être comprise comme un...) constitue
un domaine D continu, à chaque point M du domaine on affecte
une densité
(La densité est un nombre sans dimension, égal au rapport d'une masse d'une
substance homogène à la masse du même volume d'eau pure à la température de
3,98 °C.) g(M) où g est une
fonction continue (un champ (Un champ correspond à une notion d'espace
défini:) scalaire). Le barycentre est alors le point G
tel que
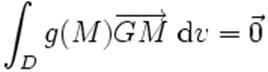 dans l'espace ou dans l'espace ou 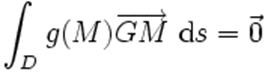 dans
le plan . dans
le plan .
Si
les points M ont pour coordonnées (x1;x2,x3) la fonction de densité
s'écrit g(x1,x2,x3)
et les coordonnées de G s'écrivent
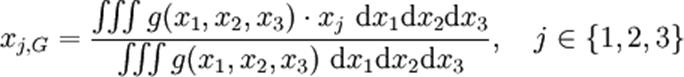
Si
l'on se ramène à une dimension, ou bien si l'on considère chaque coordonnée
séparément, on retrouve la formule de la moyenne (Il y a plusieurs façon de calculer une moyenne d'un
ensemble de nombres. Celle qu'il convient de retenir dépend de la grandeur
physique que représentent ces nombres. Lorsque, dans...)
pondérée :
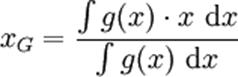
Développements physiques
Centre d'inertie
En
mécanique, le centre d'inertie d'un corps correspond au barycentre des
particules qui composent le corps en question ; chaque particule étant
pondérée par sa masse propre. C'est donc le point par rapport auquel la masse
est uniformément répartie.
Dans
le cas d'un corps continu  ,
on emploie comme fonction de pondération la masse
volumique (Pour toute
substance homogène, le rapport de la masse m correspondant à un volume V de
cette substance est indépendante de la quantité choisie : c'est une...)
ρ du corps. Dans ce cas, la position du centre d'inertie G est défini par la
relation suivante (O étant un point
quelconque de l'espace) : ,
on emploie comme fonction de pondération la masse
volumique (Pour toute
substance homogène, le rapport de la masse m correspondant à un volume V de
cette substance est indépendante de la quantité choisie : c'est une...)
ρ du corps. Dans ce cas, la position du centre d'inertie G est défini par la
relation suivante (O étant un point
quelconque de l'espace) :
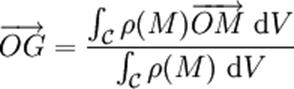 ou ou 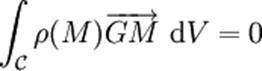
Le
centre d'inertie ne dépend donc que de la masse volumique et de la forme du
corps. C'est une caractéristique intrinsèque.
Une
propriété étonnante du centre d'inertie est
|
|
|
|
Rappel
de cours:
» G barycentre de {(A , α) (B , β)} existe si et seulement si : α + β
≠ 0
» 1. Pour construire le barycentre de trois points, il est
pratique de recourir à un barycentre partiel. De cette manière, placer un
barycentre de trois points revient à placer deux barycentres de deux points.
Pour déterminer le barycentre partiel à utiliser, il est recommandé de
sélectionner un couple de points faisant apparaître un isobarycentre (en
veillant à ce que la somme des coefficients soit non nulle, pour que le
barycentre partiel existe).
» 1. Pour placer le barycentre G de {(A ,
α) (B , β)} , on utilise la formule : AG→ =
AB→
» 1. Par propriété d’homogénéité du barycentre, pour tout réel
k non nul, si G est barycentre de {(A , α) (B , β)} , alors G est barycentre de {(A , kα) (B , kβ)} .
» 2. La réciproque de la propriété d’associativité permet de
remplacer un point pondéré d’un système par les points dont il est lui-même
barycentre. Cette propriété s’applique notamment pour remplacer (A , k) par
{(A ,a) (A , b)} avec a + b = k et k ≠ 0 .
» 2. G isobarycentre des points A , B et C signifie que :
G barycentre de {(A , k) (B , k) (C , k)} , avec k ≠ 0
L’isobarycentre de deux points est le milieu du segment formé par ces deux
points.
» 2. Le barycentre de deux points appartient à la droite formée par
ces deux points.
|
|
|
|
|
|
|
|
On donne
des points fixes « A , B , C , D,.. » et
des nombres algébriques :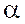 ; ;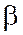 ; ;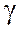 ; ;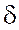 ;…. On écrit
l’opération ;…. On écrit
l’opération
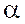  + + 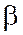 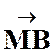 + + 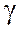 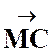 + + 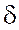 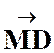 +… qui combine la multiplication d’un vecteur par un
scalaire avec la somme géométrique , +… qui combine la multiplication d’un vecteur par un
scalaire avec la somme géométrique ,
Si en particulier , dans le cas où : « 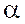 + + 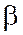 + + 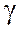 + +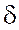 + … + …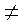 0 » 0 »
Il existe
un point « G » unique tel
que :
(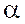 + + 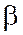 + + 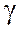 + +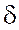 + …) + …) 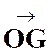 = = 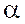 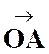 + + 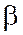 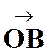 + + 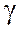 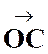 + + 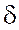 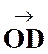 +… ( 1 ) et que l’on appelle
« barycentre » des points
« A,B,C,D,… »affectés des coefficients +… ( 1 ) et que l’on appelle
« barycentre » des points
« A,B,C,D,… »affectés des coefficients 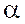 ; ;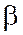 ; ;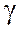 ; ;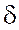 ;…. ;….
Le point
« O » est un point arbitraire et en prenant « G » en
« O » la relation (1) s’écrit aussi :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A , B et C sont trois points non alignés du plan.
G est le barycentre des points pondérés (A , 8) (B , 4) et (C , 6) .
H est le barycentre des points pondérés (A , 10) (B , 4) et (C , 6) .
Le point I est le milieu du segment [AB] .
Le point J est le milieu du segment [AC] .
1. Construire la figure.
2. Montrer que les points H, I et J sont alignés.
3. En déduire le point d’intersection des droites (IJ) et (AG) .
|
|
|
|
Corrige :
Pour placer les barycentres G et
H , on peut utiliser la propriété des barycentres partiels (également appelée
propriété d’associativité) afin de faciliter la construction.
• Placer le point G
G est le barycentre des points pondérés (A , 8) (B , 4) et (C , 6) .
On appelle K le barycentre des points pondérés (A , 8) et (B , 4) , qui
existe car 8 + 4 ≠ 0 .
Par associativité du barycentre, G est alors barycentre des points (K , 8 +
4) et (C , 6) .
On peut donc placer le point K puis placer le point G .
Placer le point K
K barycentre des points (A , 8) (B , 4) ⇔ K
barycentre des points (A , 2) (B , 1) , par homogénéité du barycentre.
D’où : 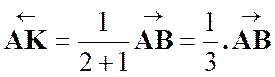
Placer le point G
Finalement, G est barycentre des points (K , 12) (C
, 6) , ou encore (K , 2) (C , 1) par homogénéité.
D’où : 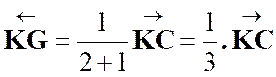
• Placer le point H
H est le barycentre des points pondérés (A , 10) (B , 4) et (C , 6) .
On appelle L le barycentre des points pondérés (B , 4) et (C , 6) , qui
existe car 4 + 6 ≠ 0 .
Par associativité du barycentre, H est alors barycentre des points (A , 10)
et (L , 4 + 6) .
On peut donc placer le point L puis placer le point H .
Placer le point L
L barycentre des points (B , 4) (C , 6) ⇔ L
barycentre des points (B , 2) (C , 3) , par homogénéité du barycentre.
D’où : 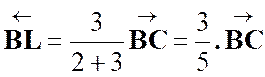
Placer le point H
Finalement, H est barycentre des points (A , 10) (L , 10) : H est donc
le milieu du segment [AL] .
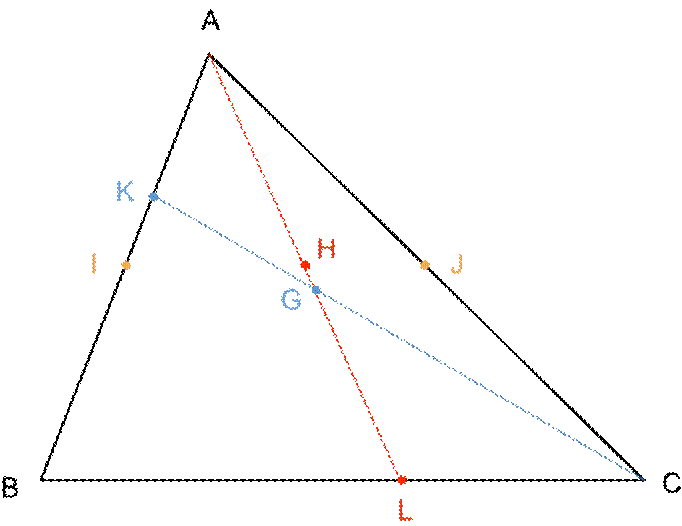
2. Pour démontrer que les points H , I et J sont alignés, on peut
montrer que H est barycentre des points I et J .
On sait que H est barycentre des points (A , 10) (B , 4) (C , 6) .
Pour tout couple de réels (a , b) tels que a + b ≠ 0 : aAA→ + bAA→ = 0→
Par réciproque de la propriété d’associativité du barycentre, on a
donc :
H barycentre des points (A , 6) (A , 4) (B , 4) (C , 6) , car A est
barycentre des points (A , 6) (A , 4) .
Or :
• I milieu de [AB] ⇔ I
barycentre des points (A , 4) (B , 4)
• J milieu de [AC] ⇔ J
barycentre des points (A , 6) (C , 6)
Par associativité du barycentre, on en déduit que : H est le barycentre
des points (I , 8) (J , 12) .
Or le barycentre de deux points appartient à la droite formée par ces deux
points.
Le point H appartient donc à la droite (IJ) .
Les
points H , I et J sont donc alignés.
3. On vient de montrer que le point H appartient à la droite (IJ) .
Il semble que le point H appartienne également à la droite (AG) , ce que l’on
va tenter de démontrer.
On sait que H est le barycentre des points (A , 10) (B , 4) (C , 6) .
Par réciproque de la propriété d’associativité du barycentre, on a donc, de
la même manière que précédemment :
H barycentre des points (A , 2) (A , 8) (B , 4) (C , 6) , car A est
barycentre des points (A , 2) (A , 8) .
Or, on sait que G est la barycentre des points (A , 8) (B , 4) (C , 6) .
Par associativité du barycentre, on en déduit que : H est le barycentre
des points (A , 2) (G , 18) .
Or le barycentre de deux points appartient à la droite formée par ces deux
points.
Le point H appartient donc effectivement à la droite (AG) .
Finalement, le point H appartient aux deux droites non parallèles (IJ) et
(AG) .
Le
point H est donc le point d’intersection des droites (IJ) et (AG) .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
On
introduit ici un nouvel outil, particulièrement performant : le
barycentre d'un système de points pondérés du plan ou de l'espace.
Outre sa puissance pour résoudre des problèmes de mathématiques, le barycentre
a de nombreuses applications, par exemple dans le domaine des statistiques
(notion de moyenne pondérée) ou en physique. D'ailleurs, quand s'est posée la
question de savoir si le calcul vectoriel pouvait s'étendre à l'espace, ce
sont des physiciens comme Gibbs ou Heaviside qui ont apporté une partie des
réponses.
1. Que faut-il
savoir sur le calcul vectoriel dans l'espace ?
On
retrouve dans l'espace les mêmes règles de calcul vectoriel que dans le plan
(vecteurs colinéaires, relation de Chasles ).
La seule nouveauté est la notion de vecteurs coplanaires.
Trois vecteurs de l'espace sont coplanaires si et seulement si l'un d'entre
eux peut s'exprimer comme combinaison linéaire des deux autres, c'est-à-dire
que les vecteurs 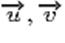 et et
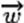 sont coplanaires si et seulement
si il existe deux réels a et b tels que sont coplanaires si et seulement
si il existe deux réels a et b tels que 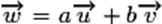 . .
Test n°1
2. Comment définir
le barycentre d'un système de points pondérés du plan ou de l'espace ?
• On commence
par définir le barycentre d'un système de deux points pondérés.
Si A et B sont deux points distincts, a et b deux réels dont la
somme n'est pas nulle, il existe alors un unique point G tel que 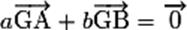 . .
Ce point s'appelle le barycentre des
points A et B affectés des coefficients respectifs a et b.
• Dans
le cas où les coefficients sont non nuls et égaux, le point G est appelé isobarycentre de A et de B. On remarque que l'isobarycentre
de A et de B n'est autre que le milieu du segment [AB].
• La
notion de barycentre, définie ci-dessus pour deux points, se généralise à un
nombre quelconque de points. Ainsi, si A, B et C sont trois points distincts,
et a , b et c trois réels dont
la somme n'est pas nulle, il existe un unique point G tel que 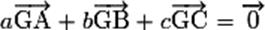 . Ce point est le barycentre des
points A, B et C affectés des coefficients respectifs a ,
b et c. . Ce point est le barycentre des
points A, B et C affectés des coefficients respectifs a ,
b et c.
Remarque
Si les points
A, B et C ne sont pas alignés, l'isobarycentre de A, B et C est le centre de
gravité du triangle ABC.
Test n°2Test n°3
3. Quelles sont les
principales utilisations du barycentre en géométrie ?
On
retiendra quatre utilisations essentielles du barycentre
en géométrie :
– pour montrer que trois points sont alignés, on fait apparaître l'un d'entre
eux comme le barycentre des deux autres ;
– pour montrer que quatre points sont coplanaires, on fait apparaître l'un
d'entre eux comme le barycentre des trois autres ;
– pour montrer que des droites sont concourantes, on montre que ces droites
passent par des barycentres partiels obtenus en regroupant de différentes
manières les mêmes points pondérés. Le point de concours des droites est
alors le barycentre des points pondérés considérés ;
– on utilise enfin le barycentre pour réduire une somme vectorielle de la
forme 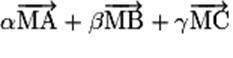 lorsque lorsque 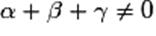 ,
par exemple dans les recherches d'ensembles de points. ,
par exemple dans les recherches d'ensembles de points.
4. Quelles
propriétés du barycentre faut-il connaître ?
Il y a
deux propriétés essentielles du barycentre à retenir.
• Homogénéité.
Si G est le barycentre de 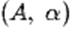 et et 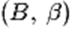 ,
alors G est aussi le barycentre de ,
alors G est aussi le barycentre de 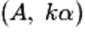 et
de et
de 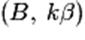 ,
pour tout réel k non nul. ,
pour tout réel k non nul.
• Associativité.
Pour trouver le barycentre G de n points, on peut remplacer plusieurs
d'entre eux par leur barycentre partiel affecté de la somme de leurs coefficients.
Cette propriété fournit une méthode de construction du barycentre d'un
système de trois points pondérés ou plus. On les regroupe deux par deux de
manière à se ramener à la construction du barycentre de deux points pondérés.
Test n°4Test n°5
5. Quels sont les
questions à se poser avant de chercher un barycentre ?
• Le barycentre existe-t-il toujours ?
Non, le barycentre d'un système de points pondérés n'existe pas toujours. Il
est indispensable que la somme des coefficients
soit non nulle.
Il faudra donc être très vigilant dans deux cas :
– lorsque les coefficients sont donnés sous forme paramétrée. Ainsi le
système de points pondérés (A, 6 + m) et (B, m) admet un
barycentre si et seulement si 6 + 2m est non nul, c'est-à-dire si et
seulement si 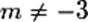 ; ;
– lorsqu'on applique la propriété d'associativité du barycentre. Ainsi, si G
est le barycentre de (A, 5), (B, 3) et (C, −3), G est
aussi le barycentre de (I, 8) et (C, −3) où I est le
barycentre de (A, 5) et (B, 3) ; mais il est impossible de
remplacer (B, 3) et (C, −3) par leur barycentre partiel
puisque la somme des coefficients est nulle ; donc le système
(B, 3) et (C, −3) n'admet pas de barycentre.
• Peut-on interpréter une égalité vectorielle en termes de
barycentre ?
On sait traduire le fait qu'un point G est le barycentre d'un système de
points pondérés par une égalité vectorielle. Réciproquement, est-il possible,
lorsqu'on connaît une égalité vectorielle, d'interpréter celle-ci en termes
de barycentre ?
La réponse est oui si l'égalité vectorielle peut être ramenée à la
forme : 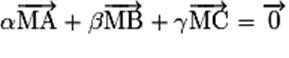 avec avec 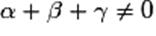 . .
Par exemple, si on connaît la relation 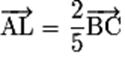 , on peut se ramener à , on peut se ramener à 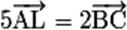 ,
puis à ,
puis à 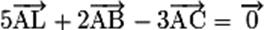 . Comme la somme des coefficients
est non nulle (elle vaut 4), cette égalité vectorielle traduit le fait que le
point A est le barycentre des points pondérés (L, 5), (B, 2) et
(C, 3). . Comme la somme des coefficients
est non nulle (elle vaut 4), cette égalité vectorielle traduit le fait que le
point A est le barycentre des points pondérés (L, 5), (B, 2) et
(C, 3).
On remarquera que cette interprétation n'est pas unique. Il est en effet
possible de faire des modifications du même type pour obtenir B, C ou L comme
barycentre des trois autres points.
• Comment caractériser les points d'une droite à l'aide des
barycentres ?
On connaît déjà la caractérisation vectorielle d'une droite : la droite
passant par A et de vecteur directeur 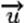 est l'ensemble des points M pour
lesquels il existe un réel k tel que est l'ensemble des points M pour
lesquels il existe un réel k tel que 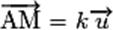 .
S'y ajoute la caractérisation barycentrique d'une droite : la droite (AB)
est l'ensemble des barycentres des points pondérés .
S'y ajoute la caractérisation barycentrique d'une droite : la droite (AB)
est l'ensemble des barycentres des points pondérés 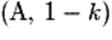 et et 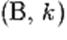 ,
où ,
où 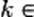 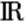 . .
À
retenir
• Le
barycentre d'un système de points pondérés n'existe que si la somme des
coefficients est non nulle.
• Le barycentre
d'un système de points pondérés n'est pas modifié si on multiplie tous les
coefficients par un même nombre non nul ; ou si on remplace certains
points par leur barycentre partiel, lorsqu'il existe, affecté de la somme des
coefficients de ces points.
• On
peut interpréter un certain nombre de notions de géométrie en termes de
barycentre : le milieu d'un segment est l'isobarycentre des extrémités
de ce segment ; le centre de gravité d'un triangle est l'isobarycentre
des sommets du triangle ; le centre d'un parallélogramme est
l'isobarycentre des sommets du parallélogramme.
•
Quatre points A, B, C et D sont coplanaires si et seulement si les vecteurs 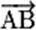 , ,
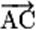 et et
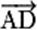 sont
coplanaires. sont
coplanaires.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Un peu d’histoire
Le barycentre qui vient du grec barus (lourd,
pesant ) et de centre, est initialement le centre
des poids. Il s’agit donc à l’origine d’une notion physique et mécanique.
Le premier à avoir étudié le barycentre en tant que centre des poids, que
l’on appelle aujourd’hui centre de gravité, est le mathématicien et physicien
Archimède au IIIème siècle avant Jésus-Christ.
Il a écrit dans son traité sur le centre de gravité des surfaces
planes :
« Tout corps pesant a un centre de gravité bien défini en lequel tout le
poids du corps peut être considéré comme concentré. »
Son principe des moments et des leviers lui a permis de construire assez
simplement le barycentre O de deux points de masses m1 et m2 différentes.

Pour que l’équilibre soit atteint, il faut que les moments m1OA et m2OB
soient égaux. Cette condition se traduit par l’égalité vectorielle :
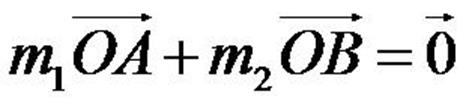
Point pondéré, point massif
Définition
Un point pondéré est un couple (A, a) où A est un point du plan ou de
l’espace et a est un nombre réel quelconque.
Un point pondéré est aussi appelé point massif ou point coefficient.
Le nombre réel a est appelé masse ou poids ou
coefficient du point A.
Barycentre de deux points
Théorème et Définition
Soient
(A, a) et (B, b) deux points pondérés tels que 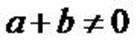 . .
Alors, il existe un unique point du plan noté G tel que
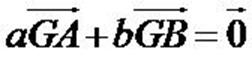
Ce point G est appelé barycentre des points pondérés (A ,
a) et (B , b).
On dit aussi que G est le barycentre des points A et B affectés des
coefficients a et b.
Existence et unicité du
barycentre
Démonstration
On
cherche un point G vérifiant
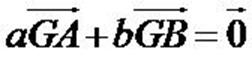
D’après la relation de Chasles, on a
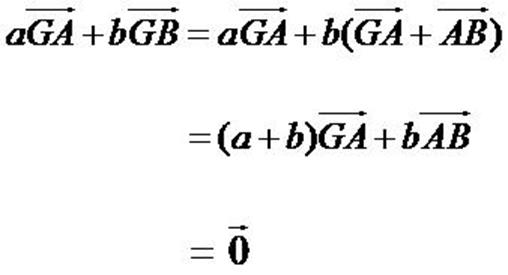
On en déduit
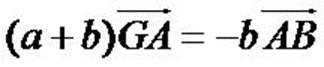
c’est-à-dire
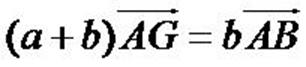
et
puisque 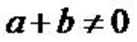
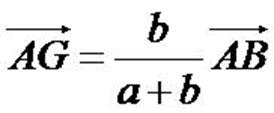
Il
existe donc un unique point G vérifiant
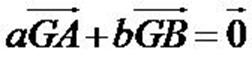

Point G
Sur la
figure les vecteurs  et et 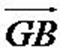 sont
opposés. On a donc sont
opposés. On a donc 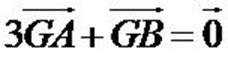
ce qui signifie que G est le barycentre des points pondérés (A, 3) et (B,1) car 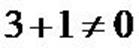

Remarques
1) Si a+b=0 on ne peut pas définir le barycentre de (A, a) et
(B, b).
2) Si 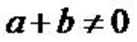 ,
le barycentre de (A, a) et (A, b) est le point A lui-même. ,
le barycentre de (A, a) et (A, b) est le point A lui-même.
Isobarycentre
Définition de l’isobarycentre
Pour tout nombre réel a non nul, le barycentre de (A, a )
et (B, a) est appelé isobarycentre de A et B.
Propriété
L’isobarycentre
de A et de B est milieu du segment [A B].
Démonstration
Si G est l’isobarycentre de (A, a) et de (B, a) avec 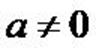 ,
alors on a ,
alors on a 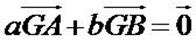
c’est-à-dire 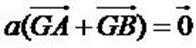
Puisque 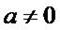 ,
on en déduit ,
on en déduit 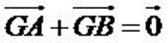
et donc 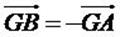
ce qui montre que G est le milieu du segment [AB].
Remarque
Le préfixe iso signifie égal.
L’isobarycentre de deux points est le barycentre de ces points affectés
de masses égales.
Homogénéité du barycentre
Propriété
On ne change le barycentre de deux points massifs en multipliant ou en
divisant les coefficients par un même nombre non nul.
Démonstration
Soient A et B deux points et a et b deux nombres réels tel que
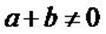 . .
Soit k un nombre réel non nul et soit G le barycentre de (A, ka) et (B, kb).
Alors on a 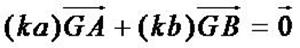
si et seulement si 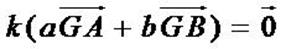
et puisque 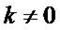 , cela équivaut à
, cela équivaut à 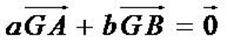
ce qui montre que G est le barycentre de (A, a) et de (B, b).
Propriétés du barycentre
Exemple
Le
barycentre de (A, 2) et (B, 3) est aussi celui de (A, 1) et (B, 3/2), celui
de (A, 2/3) et (B, 1), celui de (A, 4) et (B, 6),…
►Propriétés du barycentre
• Si A
et B sont deux points distincts tout barycentre G de (A, a) et (B, b) avec 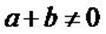 appartient
à la droite (AB). appartient
à la droite (AB).
• De plus, si a et b sont de même signe , le
barycentre G appartient au segment [AB]
Démonstration
• On a vu que si G est le barycentre de (A, a) et (B, b) avec 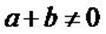 , ,
alors on a 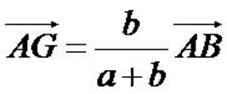
donc les vecteurs 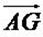 et et 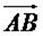 sont
colinéaires et les points A, B et G sont alignés. sont
colinéaires et les points A, B et G sont alignés.
• Si a et b sont de même signe, on peut se ramener en utilisant l’homogénéité
du barycentre au cas où a et b sont tous les deux positifs.
Supposons donc a et b positifs
On a alors 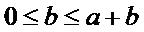
et comme 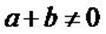 , ,
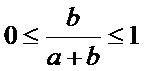
L’égalité 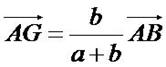 et
les inégalités et
les inégalités 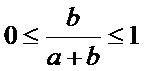
entraînent que le point G appartient au segment [AB].
Propriété de réduction
Soient (A, a) et (B, b) deux points pondérés
tels que 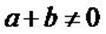 et
soit G leur barycentre. et
soit G leur barycentre.
Alors, pour tout point M du plan ou de
l’espace, on a 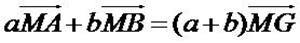
Démonstration
Pour tout point M, on a, d’après la relation de Chasles :
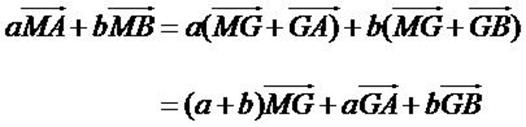
Or G est le barycentre de (A, a) et (B, b) donc 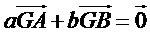
d’où 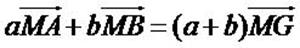
Exemple
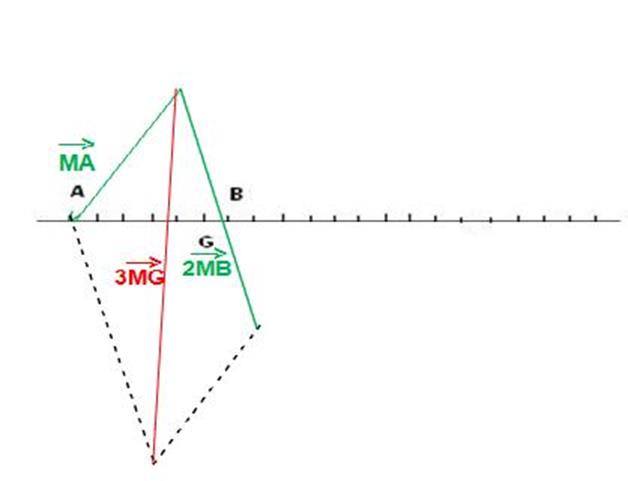
G est le barycentre de (A, 1) et (b, 2 ) car
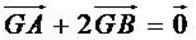
Et on a 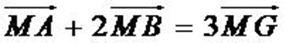
Remarques
1 ) Il s’agit d’une propriété importante du barycentre qui
permet de remplacer une somme vectorielle par un seul vecteur.
2 ) Si a+b
=0, alors (A, a) et (B, b) n’ont pas de barycentre ; dans ce cas on a
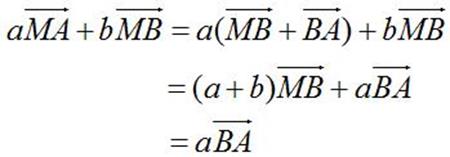
Lorsque a+b = 0, le vecteur  est donc indépendant du point M choisi.
est donc indépendant du point M choisi.
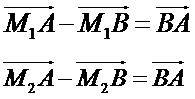
Coordonnées
du barycentre dans un repère
► Dans le plan
Soit 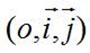 un
repère du plan. un
repère du plan.
Soient A et B deux points du plan de coordonnées respectives
(xA, yA) et (xB , yB) dans le repère 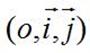 . .
.
Alors, le barycentre G de (A, a) et (B, b) avec a+b
≠ 0 a pour coordonnées
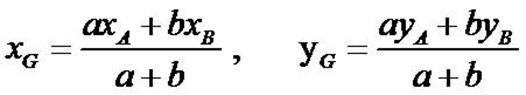
Démonstration
En utilisant la propriété de réduction en prenant M=0, on a
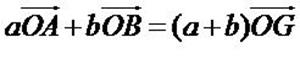
d’où
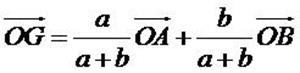
Les vecteurs 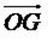 et et 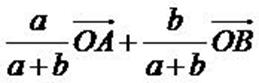 étant égaux, ils ont les mêmes coordonnées dans le repère
étant égaux, ils ont les mêmes coordonnées dans le repère 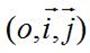 . .
Démonstration
Le vecteur 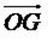 a pour coordonnées
a pour coordonnées 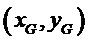 et
le vecteur et
le vecteur 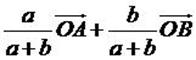 a pour coordonnées
a pour coordonnées
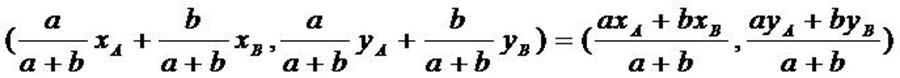
d’où les coordonnées de G
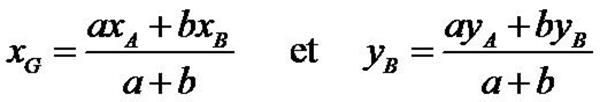
Coordonnées du barycentre dans un repère
►Dans l’espace
Soit 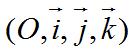 un
repère de l’espace. Soient A et B deux points de un
repère de l’espace. Soient A et B deux points de
l’espace de
coordonnées respectives (xA, yA,
zA) et (xB, yB, zB) dans le
repère 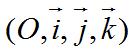 . .
Alors, le barycentre G
de (A, a) et de (B, b) avec a+b ≠ 0 a pour
coordonnées
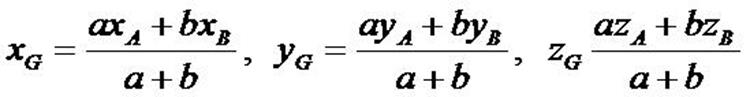
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX
AUTO FORMATIFS.
|
|
|
|
|
|
|
|
CONTROLE
|
|
|
|
|
|
|
|
|
|
|
|
EVALUATION.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|