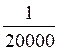Niveau 5 et niveau 4

DOSSIER : FONCTIONS LINEAIRES / Objectif cours

Pré requis :

1. Proportionnalité ( vu en primaire)	¥
2. Problèmes de proportionnalité de lla vie quotidienne	FL12
3. Fiches de travaux interdisciplinaire en arithmétique

Outils mathématique à maîtriser :

Calcul algébrique :	:SOS cours ¥
Fraction équivalente et produit en croix et règle de trois	:SOS cours ¥

INDEX :

Objectif précédent : 1°) Résumé de cours sur la fonction linéaire 2°) Cours sur la proportionnalité et l’application linéaire .

Objectif suivant : 1°) la fonction affine (présentation)

Tableau ¥

	DOSSIER : INTERDISCIPLINARITES Applications de la fonction linéaire. L’ OUTIL MATHEMATIQUE de la fonction linéaire est de la forme : y = a x ou y = m x La variable « x » est multipliée par le coefficient « k » ou « a » ou « m » s’écrit : ou  ; par convention le signe « multiplier » n’est pas représenté entre deux lettres : ou s’ écrira ou
Activités :
v Par matière		v Sujets

1°) PAR MATIERE :

	Variable « x »	coefficient (k) ou (a)	= kx ( ou ax)
Matières
Sciences :Géographie	SOS cours l’échelle
Echelle :	Distance réelle	échelle de la carte	distance lue sur la carte
Dessin industriel	D (en km)	k ou (é)	d = k D (d en km)
Sciences Physique	SOS cours le mouvement informe
(préparation concours :cours sur les vitesses)	« t » durée du parcours en	Vitesse moyenne	Distance parcourue
« cinématique »	temps en (h)	V en km ^1.h^-1 ;ou V en km / h	D = V t (D en km)
Economie	SOS cours les intérêts simples.
Comptabilité	Capital placé : C (en F)	Taux de placement t % = (t /100) = (t :100)	intérêt rapporté en1an : i = (t : 100) C
Sciences physique:
SOS cours : densité et masse volumique
Masse	Volume d’un objet V (en cm^3)	Masse volumique : d (g1.cm^-3)	Masse de l’objet : M = dV (M en g)
SOS cours : Poids et masse
P : poids	m : masse	g = 9,81	P = m g
Hydraulique	SOS cours
	Durée de l’écoulement temps en secondes	Débit moyen : d (en m^3 s^-1)	Volume écoulé : V = d t (V en m^3)
Commerce	SOS cours
	Quantité acheté : Unité	Prix à l’unité : Pu (en €)	Prix payé : P = UPu (P en € )
Electricité :	SOS cours
Puissance	P = U I
Différence de potentiel : U	Résistance électrique : R (en ohm )	Intensité électrique : I (en ampère)	U = RI (U en volt)

Mécanique :	SOS cours	Les unités de poids	Les unités de masse
Poids (en newton) : P	Masse (en kg) : M	accélération gravitationnelle: g = 9,81 N / kg ou 9,81 N.kg ^-1	Poids : P = Mg ( P en N)
Pression (rapport du poids par la surface )
Vous pouvez compléter cette liste :

APPLICATION aux calculs : Voir sciences

2°) DEVOIR : situations problèmes , Trouver les équations des droites . (Donner la signification de y et x , le l’unité attribuée )

Domaine automobile
1 )Le prix à payer est directement proportionnel à la quantité de carburant : Pour du fuel 1,50 € /litre	y = 4,50 x "y" prix à payer , "x" le prix au litre
2 ) Un automobile estime la consommation de son véhicule à 8,2 L aux 100 km. Quelle peut être sa consommation pour : 50 km ; 150 km ; 200 km ;500 km ; « x » km	Y = 8,2 x Y consommation , x le nombre de km parcourus

3 ) Composant d’un alliage : Le duralumin contient 95 % d’aluminium , 4 % de cuivre , 0,5 % de manganèse et 0,5% de magnésium. Quelle est la masse de chacun des composants contenue dans une masse de 650 g de duralumin ?

Masse de Aluminium : 617,5 g. Masse de Cuivre 26 g. Masse de Manganèse : 3,25 g. Masse de Magnésium : 3,25 g

4 )On recouvre une plaque de 1 m² destinée à fabriquer des circuits imprimés d’une couche de cuivre de 35 microns .La masse volumique du cuivre est de 8,92 g . cm^-3

Calculer la masse de cuivre utilisée.

5 ) Un garagiste accorde une remise suivant le tableau :

Prix (€) x : 40 ;50 ; 80 ;250 ;430

Remise (€ ) y : 4 ; 5 ; 8 ; 25 ; 43

a) peut-on mettre sous la forme y =ax la relation qui exprime la remise et le prix ?

b) tracer la droite représentant la fonction

x ax ( x étant positif)

6 ) La vitesse de coupe d’une fraise est donnée par le tableau suivant :

Vitesse de rotation en tours . min^-1

( N) :250 ; 375 ; 500 ;125

Vitesse de coupe en m.min^-1 (v)

11 ; 16,5 ; 22 ; 5,5

a) peut –on mettre sous la forme y = an la relation qui lie la vitesse de coupe à la vitesse de rotation ?

représenter graphiquement la fonction nv pour n positif .

7 ) La différence de potentiel V aux bornes d’un résistor et l’intensité I du courant qui le traverse sont données par le tableau :

V (volts) : 7,5 ; 10 ; 17,5 ; 30 ; 37,5

I (ampères) : 1,5 ;2 ;3,5 ; 6 ; 7,5

Peut-on mettre sous la forme V = a I la relation qui lie la différence de potentiel à l’intensité du courant ?

Représenter graphiquement la fonction IV pour I positif .

8 ) Un ressort a 10 cm de longueur . Quand on y suspend des poids , les allongement sont donnés dans le tableau ci-dessous :

Poids (N) : 10 ; 20 ;30 ;40 ;50 60

Allongement (mm) : 20 ; 40 ;60 ; 80 ; 100 ; 120

a) Peut-on mettre sous la forme y = ax la relation qui exprime l’allongement du ressort et le poids « x » ? Tracer le graphique de la fonction obtenue.

b) Trouver graphiquement l’allongement pour les poids suivants : 15N ; 32,5N ;52 N ; 65 N

Indiquer la longueur du ressort dans chacun de ces cas .

c) trouver graphiquement le poids qui correspond à un allongement du ressort de 36 mm , 72 mm , 110 mm , 125 mm .

Vérifier par le calcul les résultats trouvés .

9 ) La relation A(t) = l₀at représente l’allongement d’une tige à la température t à partir de la longueur l₀ à la température 0°.

L’allongement d’un rail mesurant 18 m à 0° est 6,5 mm à la température de 30° C.

a) Calculer le coefficient de dilatation « a » de ce rail .

b) Représenter graphiquement la fonction : t l₀at

c) Déterminer graphiquement l’allongement du rail à 12°C , à 26°C. Vérifier par le calcul.

d) Déterminer graphiquement et par le calcul l’élévation de température qui produit un allongement de 1,1 mm ; de 4 mm.

.

10 ) Une carte géographique est à l’échelle

On désigne par « D » les distances réelles exprimées en mètres et par « d » les distances correspondantes mesurées sur la carte en mètres.

a) Ecrire la relation liant « D » à « d ».

b) La fonction d D est-elle linéaire ?

Donner sa représentation graphique lorsque « d » varie de 0 à 1 .

11 ) Un capital « x » (en € est placé pendant un an au taux d’intérêt 5,4 % ( 100 € rapportent 5,4 € en un an ) .

On rappelle que i = C tn ; «  n » est la durée du placement exprimée en années

a) Calculer l’intérêt produit si x = 10 000 €

Exprimer l’intérêt produit « y » en fonction de « x ».représenter graphiquement la fonction xy.

(Echelles : Ox : 1 cm pour 1 000 € ; Oy =1 cm pour 100 € )

12 ) Une banque attribue 10% d’intérêt .

a) Quel est le montant de l’intérêt perçu au bout d’un an si je place 1 500 € ?

b) Donner la formule qui permet de calculer l’intérêt annuel I en fonction du capital C.

Déterminer la fonction linéaire associée à cette situation.

13 ) Considérons un robinet dont le débit est de 20 litres par minute.

a) Compléter le tableau :

Temps t (min) 1 ; 2 ; 5 ; 8 ; 10 ;12

Quantité d ‘eau « q » (l) 20 ; x ;y ; z ;t ;v

On passe du temps « t » (min) à la quantité « q » (litres) par la fonction linéaire t20t.

Tracer la représentation graphique de cette fonction lorsque « t » varie de 0 à 20 .

(Echelles : sur Ox , 1 cm = 2 min ; sur Oy , 1 cm = 40 litres)

Des connaissances e n sciences sont nécessaires pour comprendre le travail demandé ; (à vous de vous informer :

14°) Calculer la mesure de la d.d.p. aux bornes d’un résistor dans les cas suivants :

calibre	Echelle	lecture	d.d.p
3 V	[ 0 ; 30 [	22 divisions
10 V	[ 0 ; 100 ]	57 divisions
300 V	[ 0 ; 30 [	25 divisions

15°) Quelle est l’intensité du courant traversant le circuit ?

Calibre	Echelle	lecture
1 A	( 0 ; 100 )	83 divisions
0,1 A	( 0 ; 100)	57 divisions

16°) Une voiture consomme 18,4 litres d’essence pour effectuer le trajet Paris - Caen ( 230 km) .Quelle sera sa consommation pour effectuer le trajet Paris - Cherbourg long de 340 km ?

Que devons nous admettre pour résoudre le problème ?

17°) La masse et le volume d’un corps sont deux grandeurs directement proportionnelles .Le coefficient de proportionnalité s’appelle la « masse volumique » du corps.

a) Calculer le volume d’un corps de masse 52 kg dont la masse volumique est de 23 kg /dm³

b) Calculer la masse d’un corps de volume 3,5 dm³ dont la masse volumique est de 7,8 kg / dm³.

18 ) La longueur du cercle est donnée en fonction du diamètre ; compléter le tableau suivant :

D	5	10	12	25	28,2
L

Les deux grandeurs sont-elles proportionnelles ?

19 ) Un cycliste parcourt 12km en 45mn .Un autre 17km en 50mn .Les distances parcourues sont-elles directement proportionnelles aux durées du parcours ?

20 ) Construire un triangle ABC dans lequel BC = 50mm , l’angle B =40° et l’angle C =50°

Mesurer les cotés et les angles. Les mesures des cotés sont-elles proportionnelles aux mesures des angles opposés ?

21 ) Même question pour un triangle ABC tel que l’angle A = 60° , l’angle B = 30° ,AB = 70 mm

22 ) Une voiture se déplace à la vitesse constante de 80 km.h^-1 .La distance parcourue est-elle proportionnelle à la durée du parcours ?

>>>>>>>>>>>>>>Représentations graphiques

>>>>>>>>>>>>>>>>Autres problèmes et exercices