Pré requis:

	CORRIGE	Niveau : Classe de collège : 5^ème
	Retour vers les fiches à travailler…
		Voir programme de collège 5^ème
Objectifs les égalités : vocabulaire 1EG1
égalités les égalités : vocabulaire 2 EG2
Expression algébrique (niveau 2)

ENVIRONNEMENT du dossier :

INDEX : warmaths

Objectif précédent : 1°) Développer …… 2°) Première approche : niveau V

Objectif suivant : « factoriser » Développer (suite )

· Liste des cours d’algèbre.

DOSSIER : DISTRIBUTIVITE « développer»- FACTORISER

.

Fiche 1 –Distributivité de la multiplication sur l’addition ou sur la soustraction.

Fiche 2 - Exercices et une situation problème….

Fiche 3 - Développement d’un produit.

Fiche 4 – Calcul mental.

Fiche 5 - Exemple d’utilisation de la « distributivité ».

Fiche 6 - FACTORISATION.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

(Voir objectif : identités remarquables )

Voir + : PUISSANCE « 3 » ; d’une addition ou d’une soustraction.

Fiche 1 –Distributivité de la multiplication sur l’addition ou sur la soustraction.

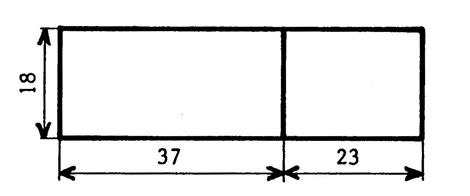
Le dessin ci-contre représente deux parcelles de jardin rectangulaires de même largeur. Les dimensions indiquées sont en mètres. On obtient une nouvelle parcelle en réunissant les deux parcelles données . On demande : Vous devez calculer la mesure de l’aire en « m² » de cette nouvelle parcelle et cela de deux façons.

1^ère façon : Vous multipliez la mesure de la largeur du nouveau jardin par la mesure de sa longueur :

Activité : ……

Sol.1

2^ème façon : Vous additionnez la mesure des deux aires de chacune des parcelles données.

Sol .2

Vous remarquez évidemment que vous obtenez le même nombre dans les deux cas .

En utilisant uniquement les nombres « 18 » , « 37 » et « 23 » vous pouvez alors écrire l’égalité :

Vous allez remplacer, dans l’égalité que vous venez d’écrire , les nombres « 18 » , « 37 » et « 23 » respectivement par trois nombres de votre choix : « ….. » ; « …… » ; «  ……. ».

Ecrivez et calculez le premier membre :

Ecrivez et calculez le second membre :

Si vous ne vous êtes pas trompé , vous devez retrouver le même nombre dans les deux cas. Vous pouvez alors écrire la nouvelle égalité où figurent les nombres que vous avez choisis.

Vous pouvez essayer avec n’importe quels nombres, l’égalité sera toujours vraie. Soit « k » , « a » , « b » représentant des nombres quelconques, vous pouvez alors remplacer vos nombres respectivement par « k » , « a » , « b » , vous obtenez :

Ce que l’on vient de faire pour l’addition est encore vrai pour la soustraction. On dira alors :

On retiendra :

La multiplication est distributive sur l’addition signifie : « k » , « a » , « b » représentant des nombres quelconques , k( a + b ) = k a + kb

La multiplication est distributive sur la soustraction signifie : « k » , « a » , « b » représentant des nombres quelconques ,( avec « a b ») k( a + b ) = k a + kb

La condition ( avec « a b »)pour être sûr d’avoir un résultat positif.

Remarque : la multiplication étant commutative, on peut écrire aussi :on peut écrire aussi : « m » , « n » ,  « p » représentant des nombres quelconques , ( m + n ) p = ……………………..mp + np Et quand «  m n » : ( m – n ) p = ……………………. m p - np

Fiche 2 : Exercices :

Activité…… On vous demande de calculer de deux façons différentes « A » donné ci-dessous. 1°) En faisant les calculs indiques ( colonne de gauche ) 2°) En utilisant la distributivité de la multiplication sur l’addition (colonne de droite). A = ( 2,4 + 0,09 + 1,42 ) 1,25

1°) méthode : A = ………………………………. A = …………………………………..

2^ème méthode : A = .….……….+ ..….……….+…….………. A = ………+ ….… + ………= ………………..

Activité…… On vous demande de calculer de deux façons différentes « B » donné ci-dessous. 1°) En faisant les calculs indiques ( colonne de gauche ) 2°) En utilisant la distributivité de la multiplication sur l’addition (colonne de droite). B= ( 7,35 - 4,5 ) 0,4

1°) méthode : B = 7,35 0,4 - 4,5 0,4 .= 2,94 – 1,8 B = …1,94 …

2^ème ) méthode : B = 2,85 …0,4 ……………………………. B = …1,14 ..

Activité …….. (situation problème)

On expédie par la poste « 30 » colis identiques. Sur chaque colis , on colle un timbre de « 20 € », un timbre à « 5 € » , un timbre à « 2 € ». Vous allez calculer , de deux façons différentes , le prix total des timbres. Info : Commencez par écrire la suite de calculs à effectuer puis effectuer ces calculs.

1^ère Façon : 30 20 + 30 5 + 30 2 = 600 + 150 + 60 = 810 2^ème Façon : 30 ( 20 + 5 + 2 ) = 30 27 = 810

Fiche 3 : Développement d’un produit.

Ecrivez la formule de la distributivité de la multiplication sur l’addition. : « k » , « a » , « b » représentant des nombres quelconques,  k ( a + b ) = k a + k b

Vocabulaire :

«  a + b » est une somme . c’est la somme dont les termes sont «a » et « b »

«  k ( a + b ) » est un produit. C’est le produit dont les facteurs sont « k » « a » , « b » . «k a » est un produit . C’est le produit de «  k » et de « a ». De même « kb » est un produit . «  k a + k b » est une somme .C’est la somme dont les termes sont « ka » et «  kb ».

Quand on remplace «  k ( a + b) » par «  ka + kb », on transforme ainsi un produit en une somme. On dit alors que l’on « développe le produit ».

Exemples :

7 ( x + y ) = 7 x + 7 y

9 ( f – 3 ) = 9 f - 27

( 3 t – 8 ) 4 z = 12 tz – 32 z

Activités :

Développez les produits suivants . ( On suppose que les soustractions sont possibles ) Effectuez les opérations qui sont possibles et utilisez les conventions d’écriture.

Corrigé

Corrigé.

6 ( c + d ) =

6c + 6d

3 ( x – z +7 ) =

3 x – 3z +21

4 ( x – 5 ) =

4 x - 20

( f + g – h ) 5 =

5 f + 5 g – 5 h

x ( 8 + y ) =

8 x + xy

6 ( xy + y – 7 ) =

6 xy + 6 y - 42

5 ( m – p ) =

5 m – 5 p

tu ( v + hr – 9 ) =

tuv + tuhr – 9 tu

( 7 a – 5 b ) c =

7 ac – 5 bc

2 x ( 3 y – 3 z + 5t ) =

6xy – 6xz+ 10 xt

Attention :

Transformez en simplifiant :

V = 4 ( 2 a + 3 b )

= 8 a + 12 b

Quelle (s) propriété(s) avez-vous utilisées pour transformer « V »

La distributivité de la multiplication sur l’addition…

T = 5 ( 2 a 3 b ) =

= 30 a b

Quelle (s) propriété(s) avez-vous utilisées pour transformer « T »

Fiche 4 – Calcul mental. ( info +++ toutes les activités sur le calcul mental )

Vous allez expliquer par écrit ce que vous pouvez faire mentalement.

Info ?

1°) Multipliez par un nombre de 1 chiffre.

74 2 = ( 70 + 4 ) 2 = 70 2 + 4 2 = 140 + 8 = 148

Faites de même pour : 47 3 =

· 47 3 = 40 3 + 7 3 = 120 + 21 = 141

· 543 3 = ( 500 + 40 + 3) 3 = 1500 + 120 + 9 = 1629

2°) Multipliez par « 9 » , « 19 » , « 29 »,……..

27 9 = 27 ( 10 – 1 )= 27 10 – 27 1 = 270 – 27 = 243

Activités :

53 9 =

53 10 - 53 1 = 530 – 53 = 477

43 19 =

43 20 - 43 1 = 860 – 43 = 817

26 29 =

26 30 - 26 1 = 780 – 26 = 754

3°) Multipliez par « 11 » , « 21 » , « 31 »,……..

45 21 = 45 ( 20 + 1 ) = 45 20 + 45 1 = 900 + 45 = 945

Activité……

17 11 =

17 10 + 17 = 187

29 21 =

29 20 + 29 =

54 31 =

54 30 + 54 =

Fiche 5 : Exemple d’utilisation de la « distributivité ».

Problème : Le produit de deux entiers est « 1598 ». Si l’on ajoute « 23 » au premier facteur, le produit devient « 2380 ». Quels sont ces nombres ?

Nota : Il est commode de désigner, les nombres cherchés par des lettres. Appelons «  » le premier entier et «  » le second.

· Traduisons l’énoncé en langage mathématique :

- « Premier terme : T 1 » : le produit des deux entiers est « 1598 » ; - se traduit par «  x y = 1598 » ( égalité « EG1 » )

- « deuxième terme : T2 » : on ajoute « 23 » au premier facteur «  » , le produit devient « 2380 » ; - se traduit par : ( + 23) y = 2380 ( égalité « EG2 » )

Nous allons maintenant faire quelques transformations : Grâce à la « distributivité », le premier membre de ( EG2 ) peut s’écrire : ( + 23) y = ( y + 23 y ) En remplaçant le premier membre de (EG2) par ce que vous venez de trouver , vous obtenez : (EG3 ) ( ) = 2380 Vous pouvez modifier le premier membre de ( EG3 ) en remplaçant «  » par «  1598 » ( voir EG1) Soit ( ) = 2380 Vous en déduisez alors que ( ) = 2380 – 1598 ; c'est-à-dire «  23 y = 782 » d’où «  y = 782 / 23 » soit « y = 34 » En remplaçant dans ( EG1) «  x y = 1598 » , « y » par ce que vous venez de trouver (34) , on obtient « 34 x = 1598 » C'est-à-dire : « x = 1598 34 » d’où « x = 47 »

Vérification : « 47 34 = 1598 » ; ( 47 + 23 ) 34 = 70 34 = 2380

Les entiers cherchés sont dans l’ordre : 47 et 34

Activité :

Le produit de deux entiers est « 899 » . Si l’on retranche « 15 » au premier facteur, le produit devient « 434 ». Quels sont ces nombres. ?

Fiche 6 - FACTORISATION. ( voir la fiche sur : la factorisation et factoriser)

« k » , « a » , « b », « m »,  « n » , « p » représentant des nombres quelconques, vous avez vu dans la « fiche 1 » que :

k ( a + b ) = ka + kb

( m + p ) n = mn + pn

( si «  a b )

k ( a - b ) = ka - kb

( m - p ) n = mn - np

( si «  m p )

· Intervertissons les deux membres de ces égalités ( au lieu de « B = A » , écrivez « A = B » )

ka + kb = k ( a + b )

mn + pn = ( m + p ) n

( si «  a b )

ka - kb = k ( a - b )

mn – np = ( m - p ) n

( si «  m p )

· En vous inspirant de ces égalités , complétez les équations ci-dessous , ( on suppose les soustractions possibles )

4 f + 4 e = 4 ( f + e )

6a – 6 b = 6 ( a- b )

I k + j k = ( l + j) k

5 r – t r = ( 5 – t ) r

6 + 3 t = 3 ( 2 + t )

7 h – 7 = 7 ( h – 1 )

«  x y + x z = x ( y + z) »

«  u w + v w = ( u + v ) w »

On dit que l’on a mis « x » en « facteur commun » ; ou que l’on a « w » comme facteur commun.

C’est ainsi que l’on a transformé une somme ( dont les termes sont des produits de facteurs) en un produit .( dont l’un des facteurs est une somme de termes).

L’opération correspondante s’appelle la « factorisation »

Attention : « a » et « b » représentant des nombres quelconques ; Il ne faut pas confondre :

3a + 3 b = 3 ( a + b )

et « 3a 3 b = 9 ab »

Ne pas confondre la somme

Avec le produit !!!

Activité …….

On veut calculer « A = 4724 64 + 276 64 ». En remarquant que « 64 » figure dans chaque terme de cette somme , on vous demande de trouver la méthode la plus rapide pour effectuer ce calcul. ( Détaillez les calculs ).

A = 64 ( 4724 + 276 ) = 64 5 000 = 320 000

Activité ……. Calculez de même : B = 4,76 37 – 4,76 12 = 4,76 ( 37 -12 ) = 4,76 ( 25 ) = 4,76 ( 100 ) / 4 = 476 / 4 = 119

Activité …….

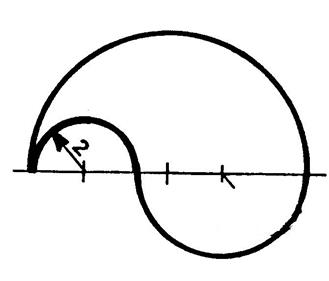
La figure ci-contre est constituée par « 3 » demi-cercles. On vous demande de calculer sa longueur « L » . ( prendre l’unité le « cm »). · Rayon du petit cercle : 2 cm . Longueur du petit demi- cercle : (( = · Rayon du cercle moyen : 3 cm . Longueur du demi- cercle moyen : (( = · Rayon du grand cercle : 5 cm . Longueur du grand cercle moyen : (( =

Longueur totale : L = =

Valeur approchée de « L » à « 0,1 cm prés » ( prendre ; «  L = 10 fois 3,14 = 31,4 »

Activité : Réduction de somme.

Activité Exemple 1 : Quand on remplace Longueur du demi- cercle moyen : on dit que l’on « réduit la somme ».

Dans la pratique , on passe directement de à 0n effectue mentalement la factorisation :

F

Activité : exemple 2 ..

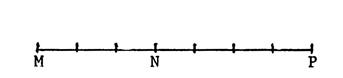
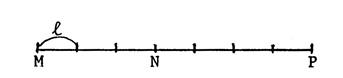
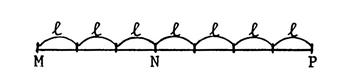
Le segment ci-contre a été par partagé en segments de même longueur « l  »

Figure 1

Figure 2

Figure 3

En vous aidant de la « figure 3 », complétez les égalités :

MP = 7 l

MN = 3 l

NP = 4 l

NP = MP – MN = 7 l - 3 l = 4 l

Activité : exemple 3 .. Réduisez :

( masse )

Monnaie

( Volume)

10 kg + 4 kg = ( 10 + 4 ) kg = 14 kg

9 € + 5 € + 3 € = ( 9 + 5 + 3 ) € = 17 €

15 m^3 – 7 m^3 = ( 15 –7 ) m^3 = 8 m^3

Remarque : « a » et « b » représentent des nombres quelconques , peut-on réduire : 7 a + 3 b ? …………………( oui : si « a » = « b »)

D’une manière générale : «  » représentant un nombre ou une grandeur quelconque. Réduisez :

TRAVAUX AUTO FORMATIFS :

CONTROLE:

1° ) Que signifie: Développer ?

2° ) Donner la condition minimum permettant de faire un développement.

3° ) Donner le modèle mathématique représentant ce minimum.

4 ° )Donner le modèle mathématique sur le développement de ( a + b ) ( c + d )

EVALUATION :

I ) Développer les expressions suivantes :
Série 1	résultat
9 ( 3 + 5 ) = (pour cet exercice uniquement ne pas effectuer les calculs!!)
3 ( x + 2 ) =
3 ( x – 2 ) =
3 ( 4 -2x ) =
4 (3x - 5 ) =
Série 2
3 x ( x + 2 ) =
3 x ( x – 2 ) =
Série 3
3 x ( 2 x + 2 ) =
3 x ( 4 x – 2 ) =
x (2y - 5x ) =
Série 4
2 ( 1 +2x )
a( 2 + b )
a(1-d)
3b(2 +1 )
3 ( x -y )
b (a^2 + c )
a (a b + c^2f)
2 xy ( x - 2y)
( x+1) [(x-3) + ( x-2 )]

II ) Développer les expressions suivantes et réduire et ordonner quand cela est possible : Nota pour « réduire » il faut avoir fait « factoriser »,il vous faudra reprendre ce travail qu’après avoir traité cet objectif !

Série 2	développer	Réduire	Ordonner
( x +1 ) ( x -2 ) =
x +5 ) ( 3x -2 ) =
( -4x +3 ) ( 5 x - 6 ) =

Série 3	développer	Réduire	Ordonner
( x +5 ) ( x + 5 ) =
( x -5 ) ( x - 5 ) =
( x +5 ) ( x - 5 ) =

Série 4	développer	Réduire	Ordonner
( 2x +3 )^2 =	Voir les I.R.
( -3x +1 ) ^2 =	Voir les I.R.

Série 5	développer	Réduire	Ordonner
( a + b )^2 =	Voir les I.R.
( a - b )^2 =	Voir les I.R.
( a + b ) ( a - b ) =	Voir les I.R.

Développer , réduire , ordonner

A = (x +5 ) ( 2 x – 1 ) – 3 (2x – 5 )

INTERDISCIPLINARITE

Géométrie

Calculer l'aire d'une surface	Longueur	largeur
Rectangle	L = x +a	l = x - b