Pré requis:
ENVIRONNEMENT du dossier:
|
Objectif précédent : 2.
Les
prismes |
Objectif suivant |
||||
|
|
|||||
|
|
DOSSIER : Liste des solides de révolutions : leur représentation en
perspective et les générations |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
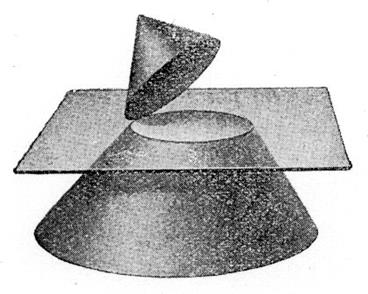
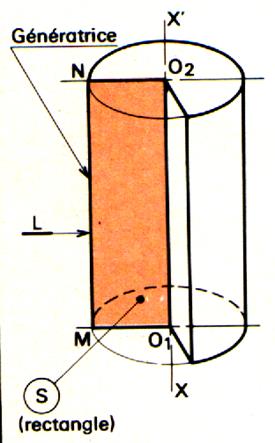
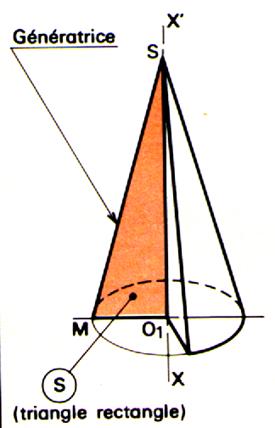
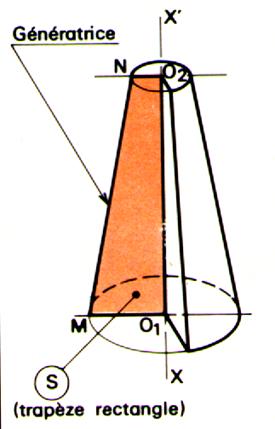
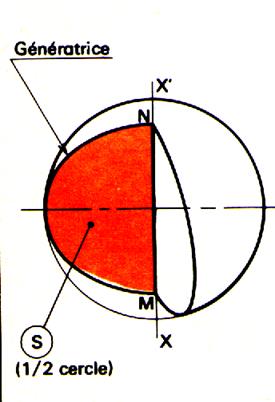
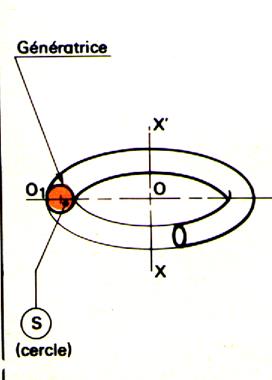
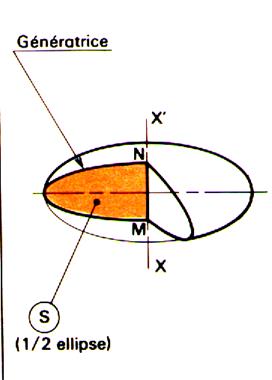
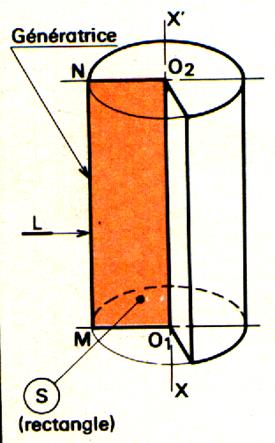
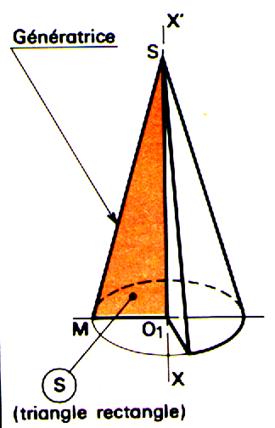
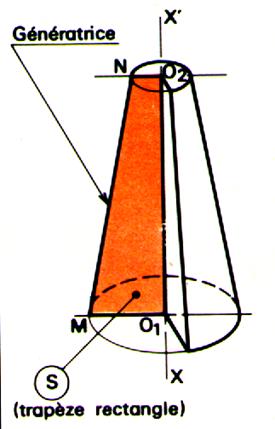
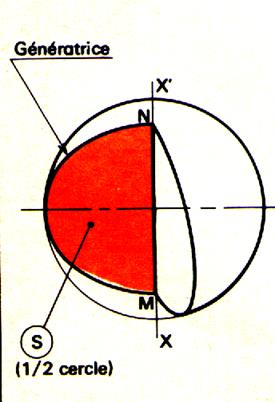
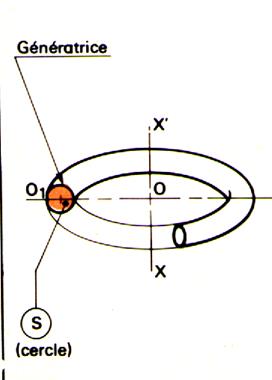
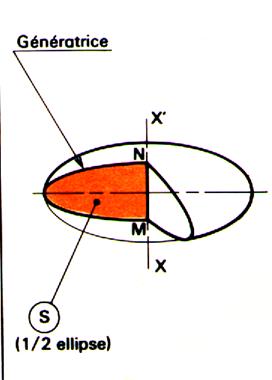
Définition « solide de révolution ». Un solide de révolution est engendré par une
surface « S » limitée par une ligne « L » , tournant
autour d’un axe xx’ de son plan et ne coupant pas « L ». Remarques : « S » engendre un volume et est appelée
« surface génératrice » « L » engendre une surface et est
appelée « génératrice » Tout point de la génératrice « L »
décrit un plan perpendiculaire à l’axe , une circonférence ayant son centre
sur l’axe xx’. Par conséquent, l’intersection d’une surface de
révolution par un plan perpendiculaire à l’axe est un cercle ou couronne dont
le centre est sur l’axe. Les principaux solides de révolution sont : |
|
|||
|
|
|
|
|||
|
TEST |
COURS |
Interdisciplinarité |
|
Informations COURS
Représentation en perspective des solides de
révolution sont :
|
|
|
|
|
|
|
|
|
|
|
|
|
Volumes particuliers : |
||
|
|
|
|
Définition « solide de révolution ».
Un solide de révolution est engendré par une
surface « S » limitée par une ligne « L »
, tournant autour d’un axe xx’ de son plan et ne coupant pas
« L ».
Remarques :
« S » engendre un volume et est appelée
« surface génératrice »
« L » engendre une surface et est appelée
« génératrice »
Tout point de la génératrice « L » décrit
un plan perpendiculaire à l’axe , une circonférence
ayant son centre sur l’axe xx’.
Par conséquent, l’intersection d’une surface de
révolution par un plan perpendiculaire à l’axe est un cercle ou couronne dont
le centre est sur l’axe.
Les principaux solides de révolution sont :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS. |
|
|
|
1° )Donner la définition
d’un solide de révolution. 2° ) Qu’appelle-t-on
« surface génératrice » ? 3° ) Qu’appelle-t-on
« génératrice » ? 4° )Citez les 6
principaux solides de révolution . 5°) que décrit chaque point d’une
génératrice ? 6°) quelle est la forme de la surface qui coupe
perpendiculairement à l’axe la surface de révolution ? |
|
|
|
|
|
|
|
|
|
Nommer les solides de révolution :
|
? |
||
|
|
|
|
|
? |
? |
|
|
|
|
|