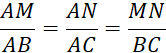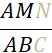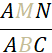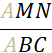|
DOC : Formation Individualisée |
DOC : Elève. |
|
DOSSIER N°
GEOMETRIE PLANE (partie 2) |
Information
« TRAVAUX » |
|
OBJECTIFS : - Savoir ……………………… |
I ) Pré requis:
|
i9 |
:i |
|
|
i9 |
:i |
II )
ENVIRONNEMENT du dossier :
Module « THALES »
GEOMETRIE PLANE: LA
RECIPROQUE DE THALES. ( au collège)
Chapitres :
|
i9 |
1°) Réciproque du théorème de
Thalès. |
:i |
|
i9 |
2°) Double application du théorème de Thalès. |
:i |
|
|
|
|
|
|
Cliquez ici :
Des problèmes et situations problèmes sur Thalès…….. |
|
IV) INFORMATIONS
« formation leçon » :
|
Travaux auto - formation. |
|
|||||
|
Corrigé |
||||||
V ) DEVOIRS
( écrits):
|
Devoir diagnostique L
tests. |
|
|
Devoir
Auto - formatif (intégré
au cours) |
|
|
Devoir Formatif « Contrôle :
savoir » ; (remédiation) |
|
|
|
|
|
Devoir sommatif. |
|
|
Devoir
certificatif : (remédiation) |
|
*
remédiation : ces documents peuvent être réutilisés (
tout ou partie) pour conclure une formation .
|
Leçon |
Titre |
|
|
|
|
1°) Réciproque du théorème de
Thalès. |
|
|||||||||
|
|
|
|
|||||||||
|
|
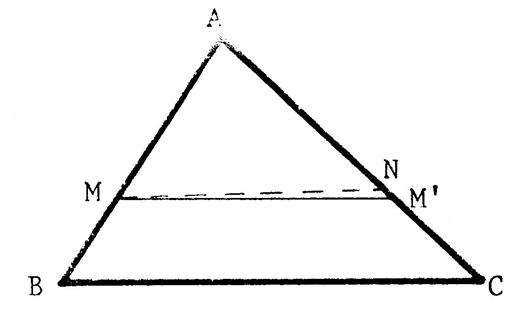
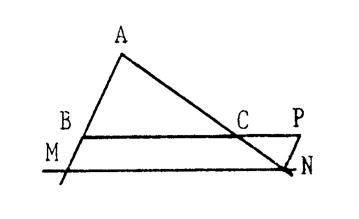
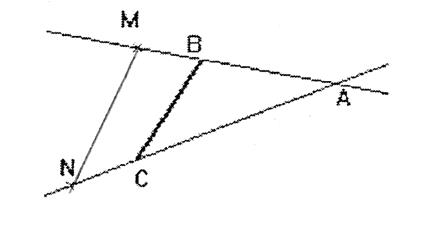
On vous donne un triangle « ABC » et deux points
« M » et « N ». « M » est sur [AB]
et « N » sur le
segment [AC] , tels que Démontrons que ( MN) est parallèle à ( BC ) Traçons par « M » la parallèle à ( BC). Elle coupe ( AC) en « M’ ». Grâce au théorème de Thalès , on peut
écrire : Or par hypothèse et par suite « AN = A M’ », et comme « N » et « M’ » sont situés sur [ AC] alors « N= M ' » Donc les droites ( MN) et ( M M’ ) sont confondues donc ( MN) est parallèle à
( BC ) |
|
|
||||||||
|
|
Remarque 1 : On pourrait faire la même démonstration
dans les deux autres cas de figure. |
|
|||||||||
|
|
Remarque 2 : |
|
|||||||||
|
|
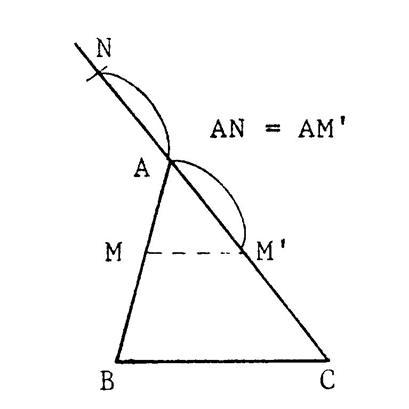
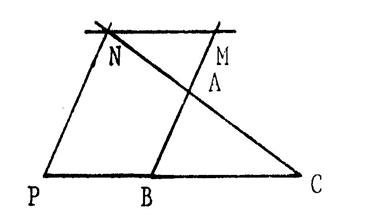
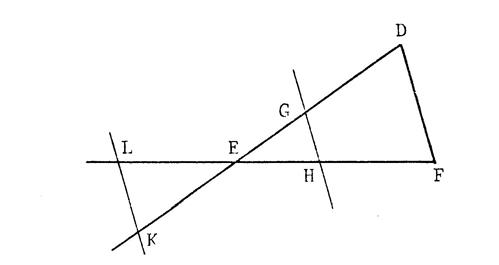
IL faut préciser que les points « M » et « N » ont
même position relative par rapport aux segments [ AB
] et
[ AC ]. En effet, sur la figure ci-contre, on a « M » est sur [ AB
] mais « N » n’est pas
sur [ AC ] et vous constatez que ( MN
) est parallèle à
( BC ). |
|
|
||||||||
|
|
Remarque 3 : |
|
|||||||||
|
|
Si par hypothèse , on a On peut donc énoncer la « Réciproque du
théorème de Thalès » |
|
|||||||||
|
|
Théorème : Dans tout triangle « ABC », « M » étant un point
de ( AB) et « N » un point de (AC), si « N » est disposé
par rapport à [ AC ] comme « M » l’est par rapport à [ A B ] et si
les longueurs des segments déterminés par « A » , « B » ,
« M » sur ( AB) sont proportionnelles aux longueurs des segments
correspondants déterminés par « A », « C »,
« N » sur ( AC ) alors les droites ( MN ) et ( BC ) sont
parallèles. |
|
|||||||||
|
|
|
|
|||||||||
|
|
Activité N° 1 : |
|
|||||||||
|
|
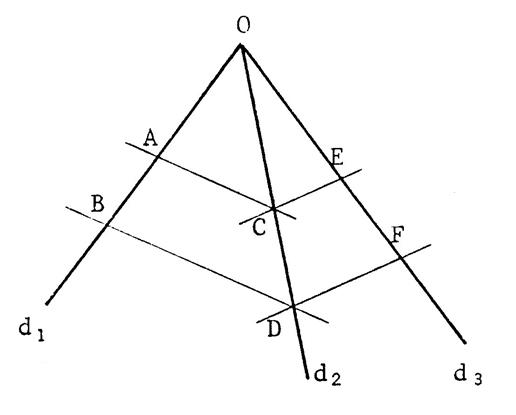
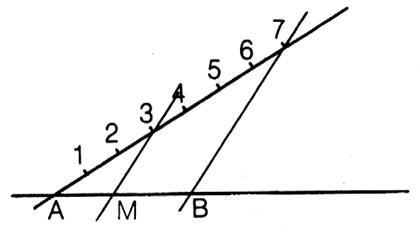
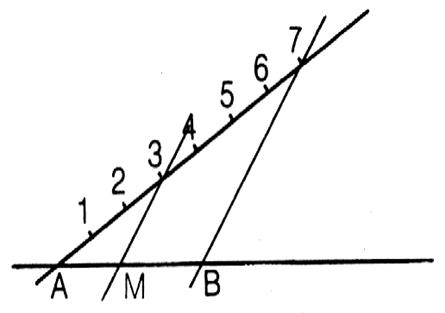
Trois droites « d1 » ,
« d2 » , « d3 » se coupent
en « O ». Deux parallèles coupent
respectivement « d1 » en un point « A »
et un point « B » et « d2 » en un point
« C » et un point « D ». Par « C » et « D » on trace deux parallèles qui coupent
respectivement « d3 »
en un point « E » et un point « F ». On vous demande de démontrer que la droite ( A E ) est
parallèle à ( BF ) · Hypothèse : ......................... ……………. ; · Conclusion : ……………………………….. ; |
|
|
||||||||
|
|
Recherche : Pour démontrer que ( AE) est parallèle à ( B F ), on doit penser au théorème
ci-dessus appliqué au triangle « OBF », à condition de savoir
que : |
|
|||||||||
|
|
Démonstration : Dans le triangle « OBD » , par
hypothèse, ( A C ) est parallèle à ( BD) , donc , grâce au théorème de Thalès
, : Dans le
triangle «
ODF » , par hypothèse , ( C E
) est parallèle à ( ………………), donc , grâce au
théorème de Thalès , : On en déduit alors
que Alors, grâce à la
réciproque du théorème de Thalès , ( AE ) et ………………..
à ( B F ) |
|
|||||||||
|
|
Activité N° 2 : |
|
|||||||||
|
|
« ABCD » est un quadrilatère convexe quelconque
. ( AC) et ( BD ) se coupent « O »
. Tracez par « O » la parallèle à ( AB
) qui coupe ( BC) en « F ». Tracez par « O » la parallèle à ( AD
) qui coupe ( DC) en « F ». 1°) Trouvez (en le démontrant) des quotients égaux à 2°) Démontrez que ( EF ) est parallèle à (
BD) |
|
|||||||||
|
|
|
|
|||||||||
|
|
2°) Double application du théorème de Thalès. |
|
|||||||||
|
|
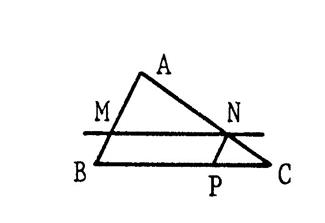
Nous reprenons ce que nous avons vu dans le chapitre sur « le théorème de Thalès »… »ABC » est un triangle quelconque. « M » est un
point de ( AB), « N » est un point de (
AC) et ( MN) est parallèle à ( BC). Nous démontrons que : Nous traçons par « N » la parallèle à ( A
B ) . Elle coupe ( BC ) en « P » . |
|
|||||||||
|
|
Ci-dessous on vous
donne les « 3 » cas de figures possibles : |
|
|||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|||||||||
|
|
Hypothèse : |
|
Conclusion : |
|
|
||||||
|
|
( M N ) / ( B C ) ( N P ) / / ( A B ) |
|
|
||||||||
|
|
|
|
|||||||||
|
|
Démonstration : |
|
|||||||||
|
|
Dans le triangle
« ABC » , par hypothèse, ( M N ) est
parallèle à ( BC) , donc , grâce au théorème de Thalès , : Dans le
triangle « ABC » , par
hypothèse , ( NP ) est parallèle à (
AB), donc , grâce au théorème de Thalès , : On en déduit alors
(par transitivité ) que D’autre part, par
hypothèse, ( MN ) est parallèle à ( BC ) et ( N P ) est parallèle à ( AB),
donc , par définition, « MNPB »
est un p………………………………., donc ses côtés
opposés ont même l………………….. donc « BP =
………………… ». Dans |
|
|||||||||
|
|
Théorème : Dans tout triangle « ABC », « M » étant un point
de ( AB) et « N » un point de (AC), si
« MN » est parallèle à ( B C ) alors : |
|
|||||||||
|
|
|
|
|||||||||
|
|
Cette situation fait apparaître deux triangles : «
AMN » et « ABC ». L’un est un agrandissement de
l’autre, leurs côtés correspondants sont « proportionnels ». |
|
|||||||||
|
|
Pour écrire les quotients
égaux, on procède de la manière suivante : On écrit l’un sous l’autre les sommets correspondants |
|
|||||||||
|
|
|
|
= |
|
= |
|
|
|
|||
|
|
Activité N° 3 : |
|
|||||||||
|
|
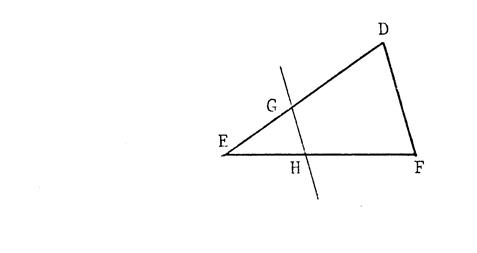
On vous donne un triangle « DEF » (l’unité est le mm). (voir la figure
ci-contre) 1°) Une parallèle à (D F ) coupe [ E D ] en « G »
et [ E F] en « H ». Ecrivez les « 3 » quotients égaux. 2°) On vous donne : « ED = 35 » , « EG = 20 » ,
« DF=56 » . Calculez « GH ». |
|
|
||||||||
|
|
3°) Une parallèle à ( DF) coupe ( ED) en
« K » , avec « K » non situé sur [ ED] et coupe ( EF) en « L » , avec
« L » non situé sur [ EF]. (voir la figure ci-contre) Ecrivez les 3 quotients égaux. 4°) « EK = 15 ». Calculez « KL » |
|
|
||||||||
|
|
|
||||||||||
|
|
« ABCD » est un trapèze « ( AB) // ( DC) ». L’unité est le
mm. Une parallèle aux bases coupe [ AD] en
« M » , [ BC] en « N » et [ BD] en « P ». « AB= 42 ; DC = 91 ; AM = 20 ; MD = 50 » . Calculez « MN » ………………….(nota :
pour cela calculez « MP » et « PN » ) . |
|
|||||||||
|
|
|
|
|||||||||
|
|
Fin du cours ( 26/02/2013) |
|
|||||||||
|
|
Cliquez ici :
Des problèmes et situations problèmes sur Thalès…….. |
|
|||||||||
|
|
|
|
|||||||||
|
Leçon |
Titre |
|
N° |
TRAVAUX d ’ AUTO - FORMATION
sur THALES |
|
TRAVAUX N° d ’ AUTO - FORMATION : CONTROLE |
|
1°) Enoncer le théorème de Thalès.
2°) Enoncer la propriété de Thalès.
3°) Enoncer la réciproque de Thalès.
|
|
Série 1 :
|
Exercice
1 :
( 3 pts.)
On donne
( en cm) : AM = 7 ; AB =
3 ; AN = 9 ; AC = 5 Les droites BC et NM sont-elles parallèles ? justifier |
|
|
Série 2
|
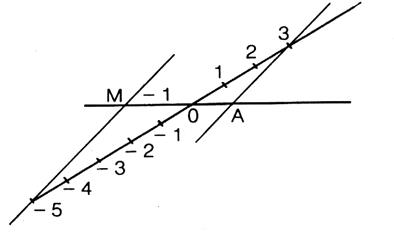
1°) quelle est la mesure de AM par rapport à AB |
|
|
|
|
|
2°) Calculer l'abscisse du point A |
|
|
|
|
|
3°) Calculer la longueur "x" |
|
|
|
|