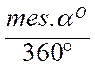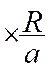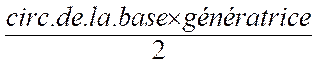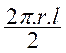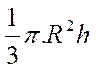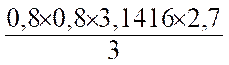Pré requis:

Les conversions

Le triangle

ENVIRONNEMENT du dossier:

Index : accueil warmaths.

Objectif précédent :

Le cône   

Objectif suivant : le tronc de cône

Info :

  1. Les unités de volumes  et de capacité.   
  2. Liste des cours sur  « le volume »

 

DOSSIER :  LE CÔNE :  calculs  d’ AIRE(S) et VOLUME

 

Chapitres :

 

 
  1. Notion : matériel intuitif

 

 
  1. Cône circulaire :

 

 
  1. Le cône de révolution

 

 
  1. Développement du cône de révolution : ( l’apothème)

 

 
  1. Angle de développement

 

 
  1. Aire latérale

 

 
  1. Surface totale

 

 
  1. Volume du cône

 

 

 

 

 

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

 

Corrigé Contrôle 

Corrigé évaluation 

 

 

COURS

 

1°)  Notion : matériel intuitif

 

Fabriquez , avec du carton, un triangle rectangle, faite le tourner sur un des côtés de l’angle droit. Imaginer – vous le solide qui est engendré par un tour complet. Quelle est la forme de la base ? Où se trouve le sommet ? Quelle est la forme de la surface latérale ?

Découper un cercle en carton ; tout autour avec du papier faites un cornet qui s’adapte à ce cercle et se termine en pointe ;Découpez ce qui dépasse et coller le cornet au cercle. Nous avons un cercle ;

2°)  Cône circulaire :

 

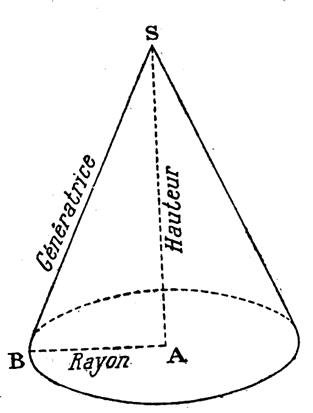
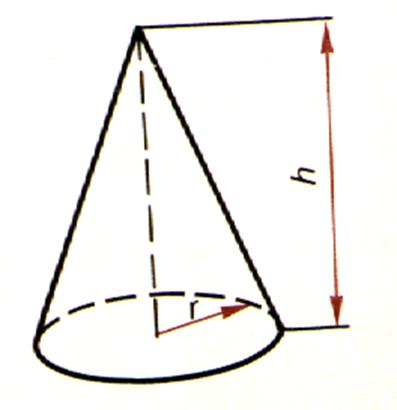
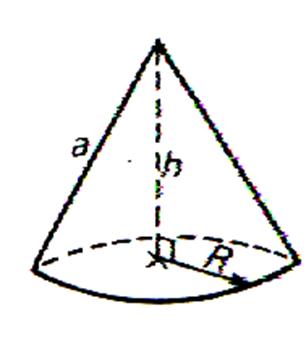
Un cône circulaire  droit est un solide engendré  par la révolution complète d’un triangle rectangle autour d’un des côtés de l’angle droit.

 

3°) Le cône de révolution

 

 

 

 

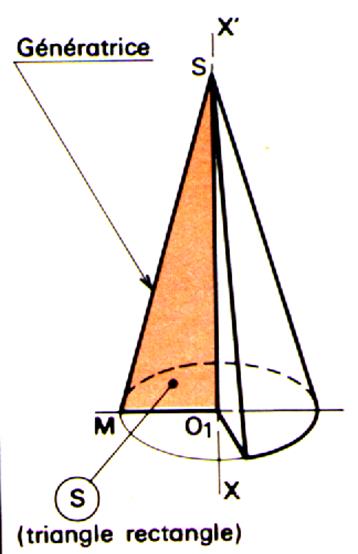
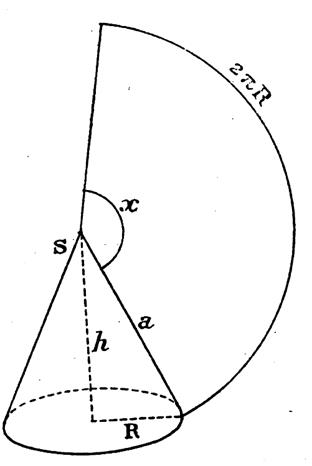
Le cône  de révolution est engendré par un triangle limitée par une ligne « SM » , dont un côté de l’angle droit tourne autour d’un axe « x x ’ » de son plan .

 

Remarques : si la base du cône est circulaire et si le sommet du cône est situé sur la perpendiculaire à la base passant par son centre le cône est droit à base circulaire.

         Un tel cône est engendré par la rotation d’un triangle rectangle autour d’un de ses cotés pris comme axe , on l’appelle pour cela cône de révolution. L’hypoténuse est la « génératrice »

         L’angle formé par l’axe et la génératrice est le « demi- angle »au sommet ; sont double est l’angle du cône.

 

La hauteur d’un cône est la perpendiculaire abaissée du sommet sur la base .

 

 

4°)  Développement du cône de révolution :

 

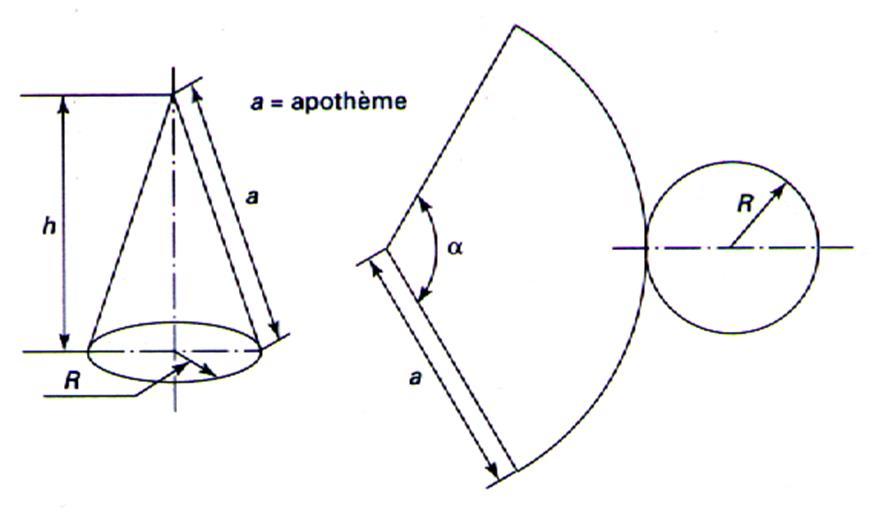
Un cône de révolution peut – être  considéré comme une pyramide régulière inscrite dont le nombre des faces latérales aurait été doublé indéfiniment.

Conséquences :

a)     les génératrices sont en même temps arêtes latérales et « apothèmes ».

b)     les résultats établis pour la pyramide sont valables pour le cône .

 

 

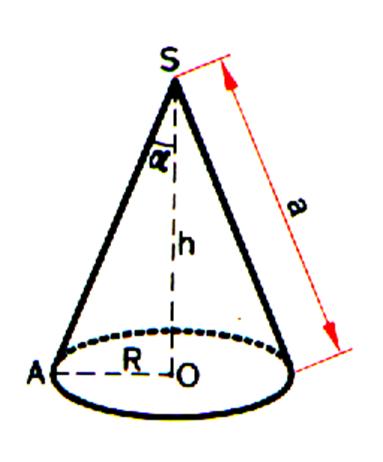
                       Le développement de la surface latérale du cône est un secteur de cercle dont le rayon est égal à la génératrice du cône.

                       L’arc de ce secteur est égal à la longueur entière de la circonférence de la base du cône.

 

5°)  Angle de développement

 

 

L’Arc AA’ peut s’exprimer de deux manières :

 

Mes. Arc AA’ = 2 p R

Ou

Mes. Arc AA’ =   2 p a (  )

 

 D’où la valeur de l’angle « a » :

Mes. a0 =  360 °

 

 

 

6°)  AIRE  LATERALE :

 

La surface latérale d’un cône droit est égale à la moitié du produit de la circonférence de la base par la génératrice.

 

 

On admettra le résultat suivant :

 

L’aire de la surface latérale d’un cône de révolution est égale au demi-produit du périmètre du cercle de base par la longueur de la génératrice .

A = p Ra

 

L’aire totale « S » s’obtient en ajoutant l’aire du cercle de base.

S = p Ra + p R2

Ou

S = p R (a + R )

 

 

 

 

Surf . latérale =

 

Ou   A =  =

 

Nota : la génératrice est appelée « apothème » du cône.

 

7°)   SURFACE  TOTALE.

 

La surface totale est la somme de la surface latérale et de la surface de la base.

 

Surf. Totale = surf. latérale + base =  p r l  + p r2  = p r ( l + r )

 

Application : Un cône a 0,80 m de rayon et 3 m d’apothème. Trouver  l’aire de sa surface latérale  et l’aire de sa surface totale.

 

1°) Surf. latérale =  p r l  = 3,1416 0,80 3 = 7,53984 m2

2°) Surface totale = 7,53984 m2 + ( 3,1416 0,80 0,80) = 9,55044 m2

 

ou surf. Totale = p r ( l + r )= 3,1416 0,80 (3 + 0,80 ) = 9,55044 m2

 

8°)  VOLUME du cône .

 

 

Le volume du cône à base circulaire est égal au tiers du produit de l’aire de la base par la hauteur.

 

V = Bh   ou  =

 

Suivant les cas ces deux lettres désignent le rayon : «  R = r »

Application :  Quel est le volume d’un cône de 0,08 m de rayon et 2,7m de hauteur ?

V = = 1,80956 m3

 

 

 

 

TRAVAUX AUTO FORMATIFS.

 

CONTROLE :

 

1 ) Donner la formule permettant de calculer le volume d’un cône .

 

 2 ) Donner la formule permettant de calculer l’aire totale  d’un cône .

 

 

 

EVALUATION

 

I )  Un cône a 0,80 m de rayon et 3 m d’apothème. Trouver  l’aire de sa surface latérale  et l’aire de sa surface totale.

 

 

 

II ) Quel est le volume d’un cône de 0,08 m de rayon et 2,7m de hauteur ?

 

III )

Calculer :

- l’aire de la surface latérale

- l’aire totale

- le volume

- la valeur de l’angle de développement du cône  avec les données suivantes :

a =

R =

h =

IV)

Calculer le volume d’un cône de 40 mm de diamètre et 30 mm de hauteur.

 

 

 

 

 

 

 

 

INTERDISCIPLINARITE

 

 

                1°) Une tour ronde est terminée par un toit conique de 7,60m de diamètre et 5,10m de côté .Combien coûtera la couverture  en zinc de ce toit à 2500 F le m2

 

                2°) Quel est en cL  la capacité d’un verre conique qui a 11 cm de profondeur et 8 cm de diamètre à l’ouverture ?

 

                 3°)  Le réservoir d’un avion a la forme d’un cylindre terminé à chaque extrémité par un cône . Les dimensions intérieures du réservoir sont : longueur du cylindre 0,60 m , diamètre 0,40 m, hauteur de cônes 0,25  m . Calculer en litre la capacité du réservoir .