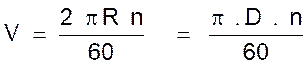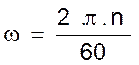|
|
|
|
|
|
||
|
|
||
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
Objectif suivant |
|
|
DOSSIER : MOUVEMENT CIRCULAIRE UNIFORME et UNIFORMEMENT VARIE |
|
|
|
·
I - Définition. : fréquence de rotation. (niv V) |
|
|
|
·
II -Vitesse moyenne linéaire ou
circonférentielle d’un point.(niv
V) |
|
|
|
·
III - Vitesse angulaire.(niv
V +) |
|
|
|
·
IV - Problèmes types |
|
|
|
Objectifs niv. V :
Savoir utiliser la relation « V = p D n » Savoir transforme la formule « V = p D n » pour calculer une fréquence de
rotation pour un mouvement circulaire (réglage machine) à partir d’une
« V » |
|
|
TEST |
COURS |
Interdisciplinarité |
|
|
|
|
|
|
|
|
|
|
|
I -
DEFINITION :
La Fréquence de rotation ( notée : « n » ou
« N ») |
|
|
|
On appelle « fréquence de rotation » le nombre de tours
effectués par un solide en une
seconde. On la note « n » et elle s’exprime en «
tr/s » ou en « tr /
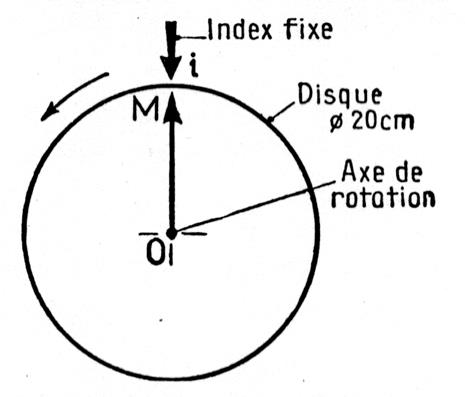
mn » Expérience : Prenons un disque monté sur l’axe de rotation d’un
moteur électrique est animé d’un « mouvement de rotation »: |
|
|
|
Le disque est animé d’un mouvement de rotation. Chacun de ces points
décrit une circonférence ayant son centre en « O » sur l’axe de
rotation. 1ère Observation : Nous comptons le nombre de tours que le disque fait chaque minute : 1ère minute : 33 tours 2ème minute : 33 tours 3ème minute : 33 tours , etc.
On constate qu’en des temps égaux , le disque fait des nombres de tours égaux ;
on dit que son mouvement est
uniforme. Sa vitesse de rotation est de 33 tr / mn. |
|
|
|
|
|
|
|
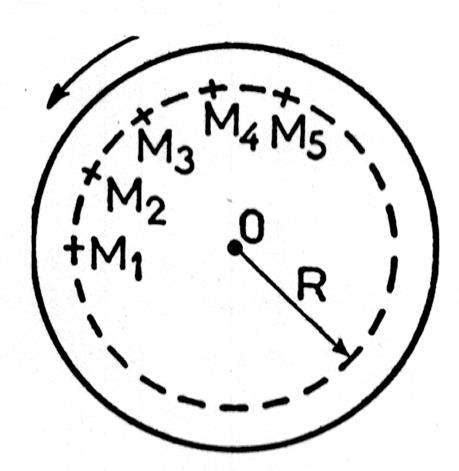
2ème
observation : Le point « M » parcours des arcs
égaux L’arc M1 M2
est égal à l’arc M2 M3 qui est égal à l’arc M3
M4 , en des temps égaux. Son mouvement
est « circulaire uniforme ». En effet : Un point quelconque « M » du disque décrit une
circonférence, son mouvement est circulaire. Il parcours , ,toujours dans le même sens ,
des arcs égaux en des temps égaux . Son
mouvement est donc circulaire uniforme. |
|
|
|
|
|
|
|
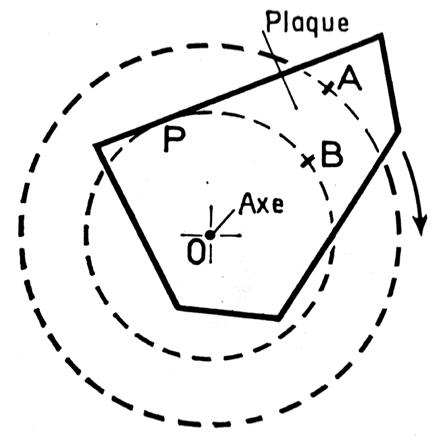
Prenons une plaque « P » de forme quelconque : |
|
|
|
Elle tourne autour de l’axe « O » d’un mouvement de rotation
uniforme. Tous les ses points , tels que
« A » ou « B »
ont un mouvement circulaire uniforme. |
|
|
|
|
|
|
|
Un point est animé d’un mouvement circulaire uniforme lorsqu’il parcourt , sur une même circonférence , toujours dans le
même sens , des arcs égaux en des temps égaux , quelques que soient ces
temps. |
|
|
|
|
|
|
|
II ) VITESSE
LINEAIRE MOYENNE ou
CIRCONFERENTIELLE d’un point.
(formule: V = p D N ) |
|
|
|
Le rayon de la circonférence décrite par le point « M »
mobile est de R = 0,10 m. En 1 tour , il parcourt la circonférence : 2 p R
= 2 ´
3,14 ´ 0,10 En 1 mn , il parcourt 33 fois cette circonférence , soit un
espace égal à : 2 ´
3,14 ´ 0,10´
33 =
20 , 724
m En 1 s. , il parcourt 20 , 724 / 60 = 0,3454 soit environ 0,35 m On exprime ces résultats en disant que le point « M » a une
vitesse linéaire ou circonférentielle de 20 , 724 m / mn
ou 0 , 35 m / s. Remarques : ►« vitesse linéaire » = une vitesse sur une ligne
(droite ou courbe) , ici sur une trajectoire qui est
une circonférence . ► « linéaire » s’oppose à « angulaire » On retiendra :la vitesse moyenne linéaire ou circonférentielle d’un point
animé d’un mouvement circulaire uniforme a la même mesure que la distance
parcourue pendant chaque unité de temps. C’est la distance parcourue en
1 minute ou en 1 seconde ; elle
s’exprime couramment en « m / mn » ou « m / s. » , parfois en « Km/h » En 1 tour (
1 tr.) la distance parcourue est : 2
p R
En « n » tr. Parcourue en 1 mn ( 60 s.) , la distance parcourue est : 2 p R n En 1 seconde ( 1s.) , la distance parcourue
est (2 p R
n) : 60 La vitesse linéaire ou circonférentielle,
exprimée en mètres par seconde , est :
où
« V » est exprimée en « m / s » ;
« R » ou « D » en « m » et « n » en tr/mn. |
|
|
|
III ) VITESSE ANGULAIRE . |
|
|
|
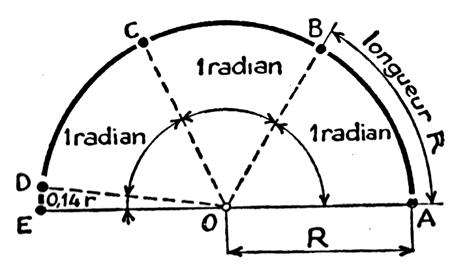
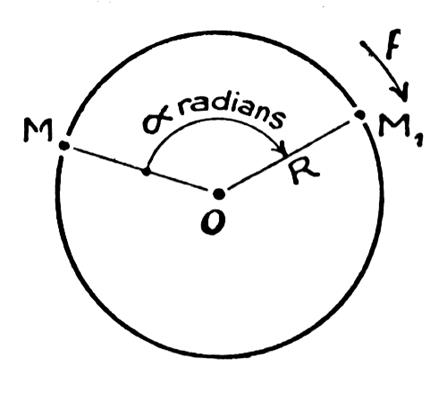
1°) Il est commode , en mécanique, d’utiliser
comme unité d’angle , non pas le degré ou le grade mais le
radian. Rappelons que le radian (symbole « rd ») est l’angle au centre
qui intercepte un arc égal au rayon. L’arc AB = rayon OA = R La demi - circonférence a une longueur de « 3,14 R », l’angle plat « AOE »
vaut « 3,14 R : R » soit « = 3,14 » rd soit = p rd |
|
|
|
|
|
|
|
On retiendra que : Un
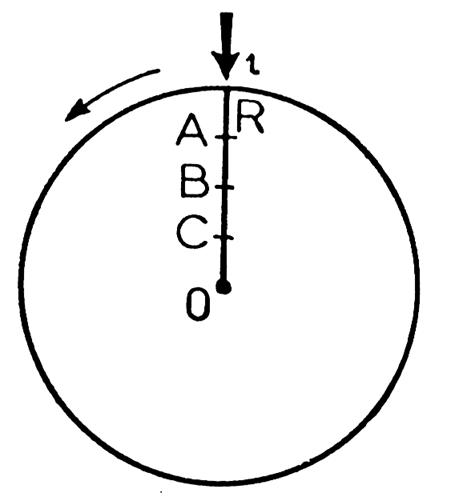
angle plat = 2 angles droits = 180 degrés = 200 grades = 3,14 radians. Expérience : Nous reprenons le disque de la première expérience. Nous traçons au
crayon le rayon « OR » situé en fac de l’indexe
« i ». Nous marquons sur ce rayon plusieurs points « A » , « B » , « C » , …… |
|
|
|
|
|
|
|
Départ : « R » face à
« i » |
|
|
|
|
|
|
|
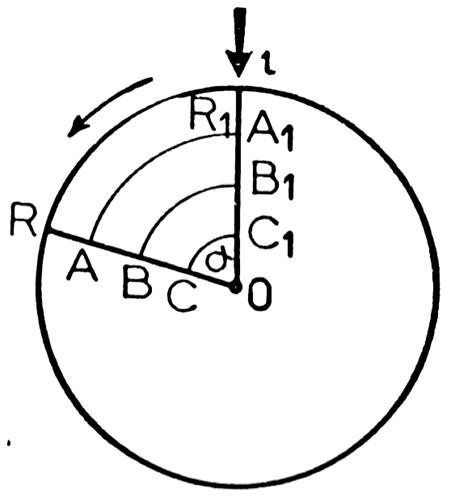
On a fait tourner le disque d‘un angle
« alpha » noté « a » |
|
|
|
|
|
|
|
les points « A »
, « B » , et « C »
n’ont pas la même vitesse linéaire, mais ils ont la même vitesse angulaire « Pourquoi ? » |
|
|
|
Le disque a tourné de l’angle «a »
correspondant à l’angle « ROR1 ». - Le point « A » a décrit l’arc de cercle
« A1A » , - le point « B » a décrit l’arc de cercle
« B1B » et - le point « C » a décrit l’arc de cercle
« C1C ». Les points
A1 , B1 , C1
sont sur le même rayon « OR1 » . Il est évident que
les points « A » , « B » , et
« C » n’ont pas décrit des espaces égaux dans le même temps. Ils
n’ont donc pas la même vitesse linéaire. Ils ont cependant une propriété commune puisque les rayons
qui les joignent au centre ont « balayé » le même angle. On exprime
ce fait en disant qu’ils ont la même vitesse angulaire « w » ( lire « oméga ») On
retiendra : La
vitesse angulaire d’un point
« M » animé d’un mouvement circulaire uniforme est mesurée
par le même nombre que l’angle , exprimé en radians
, balayé en 1 seconde par le rayon « OM » . Exemple : |
|
|
|
Quand le disque fait 33 tours / mn. Le
rayon « OM » balaie 2 demi - tours ou 2 p radians à chaque tour. En 1 mn, il balaie donc 2 ´ p ´ 33 . radians et en 1 s. , il balaie ( 2 ´
3,14 ´ 33 ) / 60 = 3,454 radians par seconde ou Si nous généralisons : Si « n » le nombre de tours par minute d’un point animé d’un
mouvement circulaire uniforme , sa vitesse angulaire
est : Où « w » est exprimée en « rd/s. »
et « n » en « tr/mn ». |
|
|
|
|
|
|
|
Il faut respecter ces unités (grandeur)pour que les calculs soient acceptés. En comparant les formules :
avec
« V » est exprimée en « m/s » ; « oméga »
en « rd /s » ; et « R » en « m » |
|
|
|
IV) PROBLEMES TYPES : |
|
|
|
|
|
|
|
Problème
1 : Un foret de 13 mm tourne à une fréquence de rotation de
500 tr/mn . Quelle est sa vitesse moyenne
« ce coupe » en m / mn . Réponse : on sait que V = p D
N Le diamètre D = 0,013 ; N
= 500 on applique directement la
formule : V = 3,14 ´ 0,013 ´
500 ; V = 20 ,
41 m / mn Problème
2 : On doit percer un trou dans un
mur avec un foret de 10 mm . La
vitesse de coupe moyenne conseillée est de
12 m / mn . Quelle doit être la fréquence
de rotation à régler sur la perceuse . Réponse : on sait que V = p D
N Le diamètre D = 0,010 ;
V = 12 on applique directement la
formule : 12 = 3,14 ´ 0,010 ´ N ; premier calcul : 12
= 0, 0314 N ; on transforme : N =
12 / 0,0314 Résultat du calcul = 382,16561 ; on réglera la
fréquence de rotation au environ de
380 tr / mn. Réponse : on sait que V = p D
N Le diamètre D = 0,013 ; N
= 500 on applique directement la
formule : V = 3,14 ´ 0,013 ´
500 ; V = 20 ,
41 m / mn Problème
3 :Le disque
dur d’un ordinateur
fait 7200 tr / mn. Quelle est la vitesse angulaire d’un point de ce
disque ? Réponse : A chaque tour du disque ,
le rayon de ce point balaie un angle de 2
p radians. En 1 mn , le rayon
de ce point balaie un angle de 2 p ´ 7200 radians. En 1 s. , le rayon
de ce point balaie un angle de (2 p ´ 7200) : 60 = 753,6 radians. La vitesse angulaire cherchée est « w =
753, 6 rd/ s.» Problème
4 :Un point
marqué sur un disque tourne à une vitesse angulaire de 3,5 rd/s . Quelle est
sa vitesse de rotation en tours par minute ? Réponse : .Le point « M » fait un tour quand
son rayon balaie un angle de 2 fois 3,14 = 6,28 radians . En 1s. , le rayon OM balaie 3,5 radians. En 1 mn. , le rayon OM balaie 3,5
radians fois 60 secondes :
3,5 ´ 60 En 1 mn. , le point « M » fait
donc : (3,5 ´ 60) : 6,28 = 33,4 tours La vitesse de rotation est donc de :
33,4 tr/ mn Problème
5 :Calculer la
vitesse moyenne linéaire circonférentielle
du point « A » sur une
plaque en rotation (figure ci dessus) sachant que OA = 18 cm et que la vitesse
angulaire est de 10 rd/s. Réponse : .Nous utilisons la formule avec
« V » est exprimée en « m/s » ; « oméga »
en « rd /s » ; et « R » en « m » nous connaissons « oméga » = 10
rd/s et R = 18 cm qui devient = 0,18 m La vitesse de rotation est donc
de 10 ´ 0,18 =
1,8 m / s Résumé :
1°)
Un point est animé d’un mouvement circulaire uniforme lorsqu’il décrit sur
une circonférence , et toujours dans le même sens ,
des arcs égaux en des temps égaux, quels
que soient ces temps. 2°)
La vitesse de rotation s’ exprime le plus souvent
par le nombre de tours effectués en 1 mn
( tr / mn ou tr . mn -1 ). 3°)
La vitesse linéaire ou circonférentielle a même mesure que
l’espace parcouru en 1 seconde ( 1 s.) Elle s’ exprime en
mètre par seconde et est donnée par la
formule
4°)
La vitesse angulaire a même mesure que
l’arc balayé en 1 s. par le rayon
joignant le centre de la circonférence
au point mobile . On l’exprime en radians par
seconde . Elle est donnée par la formule ;
5°)
On a la relation très utile :
|
|
|
|
|
|
|
|
Travaux auto formatifs. |
|
|
|
|
|
|
|
1°) Qu’appelle - t- on « Fréquence de
rotation » ? ( notée : « …… »
ou « …….») 2°) Quand dit - on
qu’un point décrit un mouvement
circulaire ? 3°) Quand dit - on
qu’un point a
un « mouvement circulaire est
uniforme » ?. 4°) Traduire : « m / mn » = « m / s. » =
« Km/h » = et « m . mn-1 » = « m . s -1 » = « Km . h-1 » = quel est le point commun à ces écritures ? 5°) A quoi est égale la vitesse moyenne linéaire ou
circonférentielle ? 6°) C’est la distance parcourue
en 1 minute ou en 1 seconde ;
elle s’exprime couramment en « …………… »
ou « ……………. » ,
parfois en « ………….. » 7°) Soit un point sur un disque : 8°) Quelle est la distance parcourue par ce point en 1 tour ( 1 tr.) ? 9°) Quelle est la distance parcourue par ce point en
1 minute connaissant le « n » tr par minute . 10 °) En déduire la distance parcourue en 1 s. 11 °) Donner la formule permettant de calculer V : La vitesse linéaire ou
circonférentielle, exprimée en mètres
par seconde , est : 12°) On donne la formule : En déduire « n » 13°) Compléter : Un angle plat = ……angles droits =
……….degrés = ……….
grades = …….. radians. 14° )
Définir : le radian ; quel
est le symbole qui le représente ? 15°) Qu’est que la vitesse
angulaire ? à quoi correspond t - elle ?
par quelle lettre la désigne - t - on ? 16°) Donner la formule permettant de calculer la vitesse
angulaire : 17°) Donner la formule qui
permet de calculer la vitesse moyenne
circulaire en fonction de la vitesse angulaire : Problèmes types : (corrigé dans le cours) Problème
1 : Un foret de 13 mm tourne à une fréquence de rotation de
500 tr/mn . Quelle est sa vitesse moyenne
« ce coupe » en m / mn . Problème
2 : On doit percer un trou dans un
mur avec un foret de 10 mm . La
vitesse de coupe moyenne conseillée est de
12 m / mn . Quelle doit être la fréquence
de rotation à régler sur la perceuse . Problème
3 :Le disque
dur d’un ordinateur
fait 7200 tr / mn. Quelle est la vitesse angulaire d’un point de ce
disque ? Problème
4 :Un point
marqué sur un disque tourne à une vitesse angulaire de 3,5 rd/s . Quelle est
sa vitesse de rotation en tours par minute ? Problème
5 :Calculer la
vitesse moyenne linéaire circonférentielle
du point « A » sur une
plaque en rotation (figure ci dessus) sachant que OA = 18 cm et que la vitesse
angulaire est de 10 rd/s. |
|