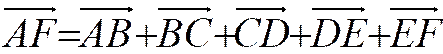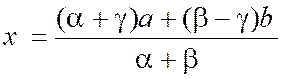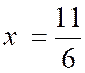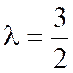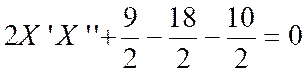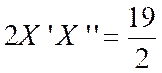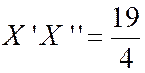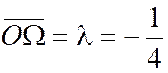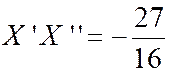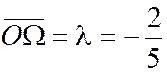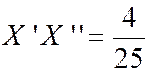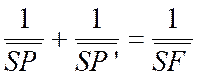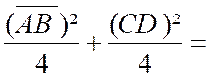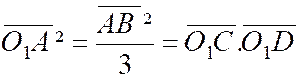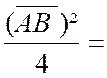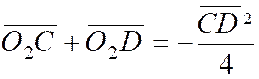1°) La relation de Châles .

2°) Changement d’origine.

Complément : 10 situations problèmes types à étudier .

1°)   La relation de  Châles :

·      A savoir :

On sait que sur un axe orienté, tout vecteur    est pourvu d’une mesure algébrique      .

L’unité de longueur ayant été choisie, la mesure algébrique exprime par sa valeur arithmétique la grandeur du vecteur et par son signe l’orientation relativement au sens positif de l’axe.

Cette mesure algébrique, dont nous admettons l’existence,est le rapport entre le vecteur   et le vecteur unitaire  de l’axe.

On pourra  écrire :       =  . .

( voir ;: norme du vecteur)

·     

Ou  Traduite au moyen des mesures algébriques ,cette relation de définition devient :

·     

Et constitue la relation de Chasles pour des points alignés.

Elle exprime que le chemin algébrique parcouru est le même que l’on aille directement de « A » vers « F » ou que partie , de « A » , on arrive en « F » après avoir pris les points «  BCDE » comme relais.

On peut écrire :

( remarque :   ou  )

C’est une relation entre des nombres algébriques . Elle est valable pour des points alignés, quels que soient leur nombre et leur ordre de succession .

Il y a avantage à l’écrire sans regarder une figure.

Problème N°1 :

S un axe orienté, relativement à une origine « O ». Les points « A » et « B » ont pour abscisses respectivement « a » et « b ».

Calculer l’abscisse « x » du point « M » tel que :                 ;   ( relation 1)

   étant trois coefficient algébriques donnés.

Solution :

Rappelons que l’abscisse d’un point « M » est  «  »

On a donc :  ;  et 

A la relation ( 1 ) appliquons la relation de Châles  , pour introduire partout l’ origine « O » 

        devient   :       ( relation 2)

N’oublions pas que la permutation  des lettres entraîne le changement de signe de la mesure algébrique. : 

Et la « relation 2 » devient :

Développons :   (relation 3)

Transposons et réduisons :

Donc , pour     :                         (relation 4)

Si par hasard : , (dénominateur du rapport )  le problème est impossible ou indéterminé.

Problème 2 : Sur un axe orienté, relativement à une origine « O », deux points « A » et « B » ont pour abscisses respectives « a » et « b » . Calculer l’abscisse du point  « M » tel que :   

indications  : Introduisons l’origine « O » :

Problème 3 : Sur un axe orienté, relativement à une origine « O », deux points « A » et « B » ont pour abscisses respectives « -7 » et « + 4 » . Calculer l’abscisse du point  « M » tel que : ?

Réponse :

2°) Changement d’origine.

La relation de  Châles est un outil pour tout ce qui concerne les changements d’origine sur un axe .

  Le point  d’origine « O » étant l’origine ancienne, et   «  «  l’origine nouvelle.

L’abscisse nouvelle «  » est connue dés que l’on connaît l’abscisse ancienne «  » et l’abscisse ancienne de la nouvelle origine «  ».

Problème 4 : Les abscisses de deux points « M’ » et « M » désignées par « x’ »  et « x’’ » satisfont à la relation.  

  (relation 1)

                                 Choisir une origine nouvelle «  » de telle sorte que , par rapport aux abscisses nouvelles  « X’ »   et «  X ‘ ’ » , la relation (1) se réduise à : « X’ +  X ‘ ’ = constante»

Solution :

Désignons par (lambda :) l’abscisse inconnue du point «  » . D’après ce qui précède :      ;    et la relation (1) s’écrit :

   ( relation 2)

Développons en respectant le groupement  «( X’ +  X ‘ ’ ) »

Regroupons :

     ( relation 4)

   Nous faisons disparaître le terme  «( X’ +  X ‘ ’ ) » en écrivant :  ;    définit l’origine «  »

Et la relation ( 3) se réduit à :

                ( relation 4)

Problème 5 : Les conditions étant les mêmes qu’au problème précédent, déterminer une nouvelle origine  «  »  pour que :

se réduise à : « X’ +  X ‘ ’ = constante»

Indications. Après application de la relation de la Châles , on obtient :  

La nouvelle origine   «  »  est définie par :

Et l’on a

Problème n°6 :Même question , mais en  partant de : 

Réponse : Nouvelle origine  «  » telle que :

Et l’on a

Problème 7 :

Les mesures algébriques de vecteurs définis par quatre points alignés « SFPP’ » sont liés par la relation :

            ( relation 1)

Que devient cette relation lorsque l’on prend  le point « F » comme origine ?

( Relation entre les abscisses de « S ; P ; P’ »)

Solution :Sous sa forme entière, la relation proposée s  ‘écrit :

             ( relation 2)

Nous introduisons partout le point « F » en utilisant la relation de Châles :

Développement :

Réduisons et remarquons que :            

il reste : 

Problème 8 :

Quatre points « ABCD » d’un même axe orienté sont tels que :

   (relation 1)

On prend l’origine « O » au milieu de AB. Que devient la relation 1 ?

Indications :

1°) Introduire le point  « O » par la relation de Châles :

2°) Développer et tenir compte du fait que « O » est le milieu de « AB »  au moyen de :    ou 

3°) On trouve :  ;

De même si « I »  est le milieu de « CD » :  

Problème 9 :

Quatre points « ABCD » d’un même axe orienté sont tels que :

   (relation 1)

Soit  O₁  et   O₂  les milieux respectifs de « AB » et « CD ». Etablir que :                  (relation 2)

Indications :

1°) Appliquer les résultats du problème n°8.

     (relation 3)

2°) Introduire  «  » au second membre de la relation 3  par la relation de Châles :

                (relation 4)

3°) Tenir compte de :

et de : 

Problème 10 : Soit « ABC » trois points fixes d’un axe et « M » un point variable de cet axe. Etablir que :

Il n’y a qu’à introduire « M » dans l’évaluation de :

Travaux auto formatifs

CONTROLE :

EVALUATION :

Reprendre les exercices du cours.