Pré requis:
|
Soustraction de deux nombres relatifs |
|
|
|
|
|
|
|
ENVIRONNEMENT
du dossier:
|
Objectif
précédent : |
Objectif suivant : |
DOSSIER LA
RELATION DE CHASLES (sur une
droite graduée)
|
|
|
|
|||||
|
|
-
Théorème
1 : (Il
existe six cas possibles ) |
|
|||||
|
|
-
Théorème 2 : |
|
|||||
|
|
-
Exemples de calculs. |
|
|||||
|
|
-
Relation de CHASLES appliquées aux mesures algébriques de
plusieurs bipoints sur une droite graduée. |
|
|||||
|
|
- RESUME : vecteur , mesure algébrique d’un
vecteur,…… |
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
2°)Application |
|
||||
INFO.
CHASLES Michel ( 1793 –1880)
Auteur
d’importants travaux de géométrie , il est surtout
connu grâce à la relation qu’il a établi et qui porte son nom :
|
·
Quels que
soient les trois points ( A ;
B ; C) d’une droite : |
|
|
·
Quels que
soient les trois points ( A ; B ; C) du
plan ; |
Il a
enseigné la géodésie (Science qui s’intéresse à la forme et aux dimensions de
la terre )à l’ Ecole polytechnique .
Ensuite
il a occupé une chaire de géométrie
supérieure à la Sorbonne.
Théorème 1 :
La mesure algébrique de la somme
de deux vecteurs consécutifs portés par un même axe est égale à la somme des
mesures algébriques de ces vecteurs.
Il
s’agit de montrer que l’égalité vectorielle ![]() entraîne l’égalité
entraîne l’égalité ![]()
Connue
sous le nom de relation de Chasles
Il existe six cas possibles :
Cas 1
![]()
![]()
![]()
A B C
![]()
Cas 2
![]()
![]()
![]()
C A B
![]()
Cas 3
![]()
![]()
![]()
B C A
![]()
Cas 4
![]()
![]()
![]()
C B A
![]()
Cas 5
![]()
![]()
![]()
C A B
![]()
Cas 6
![]()
![]()
B A C
![]()
Pour le cas « 5 » on a ,
par exemple , ![]() ;
; ![]()
D’où en transposant : ![]()
Remarque : il faut trois égalités arithmétiques pour traduire , selon les cas , la position relative de trois
points A ; B ; C en ligne droite
AC = AB +BC ;
AC = AB – BC ; ou ; AC = BC – AB
Au contraire : la relation de Châles est générale et est indépendante du sens de l’axe .
Si M , N et P , on a toujours
![]()
; ( intercaler la lettre N entre M et P qui figurent au premier membre)
quel que soit le sens suivant lequel la droite MP est orientée .
Généralisation :
La relation de
Chasles se généralise pour un nombre quelconque de vecteurs consécutifs
. Si A ; B ; C ; et
D sont alignés .
On a :

![]()
![]()
D’
où : ![]()
Théorème 2 :
la mesure
algébrique
d’un vecteur porté par un axe est égale à l’abscisse de son extrémité , diminuée de l’abscisse de son
origine .
Nous appliquons la formule de Chasles
aux trois points O , A et B
![]()
d’où ![]()
si nous désignons par « a » et
« b » les abscisses de A et de B ; nous obtenons
![]() = b – a
= b – a
Exemple de calculs.
Exemple
1 :
O A B +2 +5
![]()
![]() = b – a ; a = +
2 ; b = + 5 ;
= b – a ; a = +
2 ; b = + 5 ; ![]() = ( + 5 ) - (+2) = +3
= ( + 5 ) - (+2) = +3
Exemple
2 :
B O A - 1 +4
![]()
![]() = b –
a ; a = + 4 ;
b = -1 ;
= b –
a ; a = + 4 ;
b = -1 ; ![]() = ( -1 ) - (+4) = -5
= ( -1 ) - (+4) = -5
Relation de CHASLES
appliquées aux mesures algébriques de plusieurs bipoints sur une droite
graduée.
Quels
que soient les trois points ( A ; B ;
C) d’une droite ; ![]()
Les
bipoints (A, B) et (B,C
) sont appelés bipoints consécutifs
.
On
dira que :
La
mesure algébrique de la somme de deux
segments consécutifs est égale à la
somme des deux mesures algébriques de ces segments .
Soit
une droite :
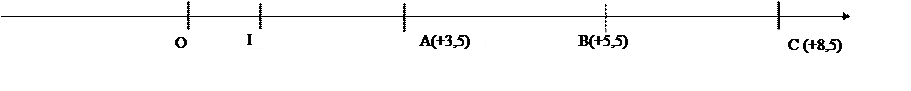
|
Vecteurs |
|
On appelle
« vecteur » un segment de droite orientée. ; …………….. Exemple : ![]()
On représente un vecteur AB par la notation : ![]() ; « A » est l’origine du vecteur et
« B » son extrémité.
; « A » est l’origine du vecteur et
« B » son extrémité.
|
Mesure algébrique d’un vecteur
. |
|
On appelle « mesure
algébrique » d’un vecteur porté sur un axe le nombre
qui a:
1°) pour valeur absolue le nombre qui mesure la
longueur du vecteur.
2°) pour signe
« + » ou « -» suivant que
pour aller de l’origine à l’extrémité du vecteur on se dirige dans le sens
positif ou dans le sens négatif sur
l’axe.
La
mesure algébrique d’un vecteur porté sur
un axe se représente par la notation : ![]()
|
|
« Relation de Chasles » |
|
Etant donnés trois
points « A » ; « B » et « C » sur un axe , quelles que soit les positions de ces points on
a :
|
|
|
|
Enoncé
équivalent : la
mesure algébrique d’un vecteur porté sur un axe est égale à l’abscisse de son
extrémité diminuée de l’abscisse de son origine.
|
|
|
Remarque : (
|
Application : l’abscisse du milieu d’un segment porté par
un axe est égale à la demi - somme des abscisses des extrémités du segment.
Généralisation : Soient « n » points « A ; B ; C ; ….H ;
K ;L » d’un axe. En procédant de proche en proche on peut
écrire :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
INTERDISCIPLINARITE
|
|
APPLICATIONS de
la relation de Chasles :
|
|
Pour chaque cas : cliquer sur le groupe de
mots « pour voir »
|
|
|
II ) Le traité vectoriel du centre de gravité
d’un triangle |
|
|
|
|
|
Travaux auto formatifs. |
|
|
|
1. Qu'appelle t on
"mesure" 2. Qu'appelle t on
"longueur " 3. Qu'appelle t on
"distance" 4. Pour quoi est utilisée la mesure algébrique ? 5. Compléter les
phrases suivantes : 6.
la mesure algébrique d ‘ un bipoint est ……………… , 7. La distance entre deux points ………………………………… 8. La longueur
entre deux points ………………………………….. 9. On dit que la mesure algébrique est une valeur
relative : quelle est le rôle des
éléments qui composent cette valeur relative ? 10.
Traduire en
langage littéral : xE - xO
= 11.
Traduire en langage
mathématique : 12.
La mesure
algébrique d ‘un bipoint ( d ’ origine B et d ’extrémité A ) est égale à la différence de l ’ abscisse de
l’extrémité A moins l ‘ abscisse de l
’ origine du bipoint B. 13.
Donnez la procédure
pour calculer la mesure algébrique d' un bipoint : Exercice n° 1:Enoncé :
Calculer Donner les deux solutions :graphique et par le calcul. Deuxième exercice: Enoncé : Calculer
Donner les deux solutions : graphique et par le calcul. |
|