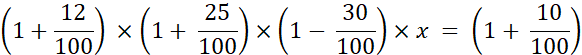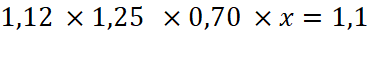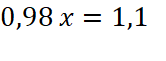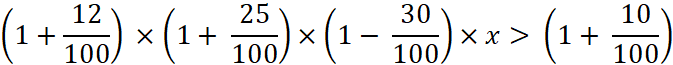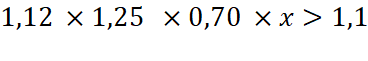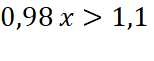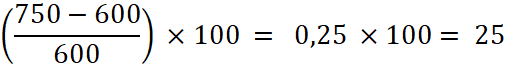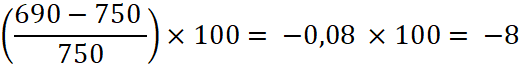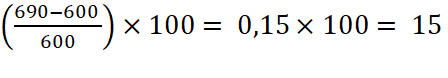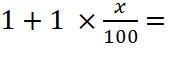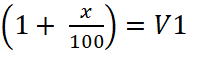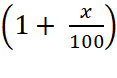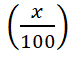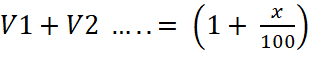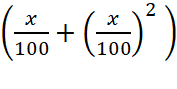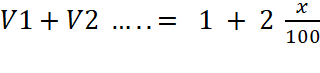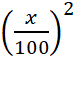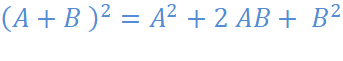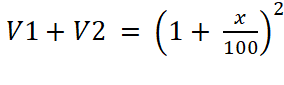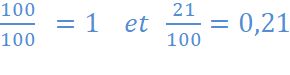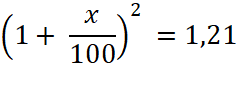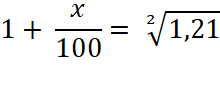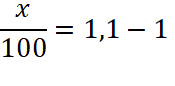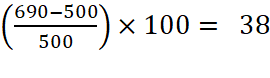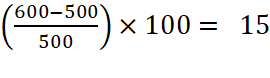Pré requis :

Les pourcentages

ENVIRONNEMENT du dossier :

Index warmaths

Objectif précédent : 1°) Intérêts notions 2°) Taux de croissance.

Comptabilité 1°)Les intérêts simples

Tableau synoptique189 Page index sur les pourcentages.

Leçon : CALCUL DE TAUX d’évolution sur plusieurs périodes.

TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité Cliquez ici sur :	Corrigé Contrôle	Corrigé évaluation
				Fiches de travaux (tertiaire)
				Calcul du taux : dos- 203)

Info. COURS

Niveau seconde et premières technologiques

si une grandeur connaît successivement plusieurs variations, on peut calculer son taux d'évolution global .

Exemple : soit une augmentation de 20 %, puis une autre de 5 % puis une baisse de 4  %. À combien s’élève la variation totale ?

Les coefficients multiplicateurs :

Dès qu’un calcul de pourcentage se profile, il faut sans plus tarder utiliser les coefficients multiplicateurs.

En l’occurrence, l'opération consiste simplement à les multiplier entre eux pour obtenir le résultat.

On sait qu’il suffit pour cela de prendre 1 et d’ajouter (ou d’enlever, c’est selon) le taux d’évolution divisé par 100.

C’est très facile dans le cas des hausses.

Pour les baisses, cela demande un léger calcul mental aux plus courageux et une calculatrice pour les autres.

Donc, d’après le cas ci-dessus on effectue les calculs suivants :

1,20 × 1,05 × 0,96 =  1,14169. La hausse globale est de 14,17 % (arrondi).

Éventuellement, la série de nombres peut être présentée sous forme d’indice .

Lorsque l’on emprunte pendant 15 ans à un taux de 3 % . Le taux étant chaque fois le même, d’une année sur l’autre , il suffit d’élever le coefficient multiplicateur à une puissance.

nota

C’est le principe utilisé dans le calcul d’intérêts composés (toujours le même taux et des intérêts reçus qui rapportent à leur tour des intérêts).

Pour connaître le taux moyen de plusieurs évolutions successives, voir (cours sur les racines énièmes).

Dans la mesure où les explications ne sont pas plus compliquées que ça, voici sans plus tarder de quoi vous exercer aux calculs d'évolutions...

Situations problèmes Types.

Situation problème N° 1 :

Un directeur commercial constate que ses ventes de tondeuses de jardin ont augmenté de 12 % au premier trimestre, puis de 25 % au deuxième trimestre (par rapport au premier) et qu’elles ont diminué de 30 % au troisième trimestre.

Question1 : Quel devrait être la progression du quatrième trimestre pour égaler l’objectif fixé pour l’année qui est de +10 % ? Arrondir à deux décimales

Autre question 2 : Quel devrait être la progression du quatrième trimestre pour dépasser l’objectif fixé pour l’année qui est de +10 % ? Arrondir à deux décimales

Corrigé :

( premier cas ) Question1 :

Nous appelons le coefficient multiplicateur du quatrième trimestre et utilisons les coefficients multiplicateurs dans une équation.

Il s’ensuit que

Donc  = 1,1224. Les ventes du quatrième trimestre doivent progresser de 12,24 %

( second cas ) Question 2 :

Nous appelons le coefficient multiplicateur du quatrième trimestre et utilisons les coefficients multiplicateurs dans une inéquation.

Il s’ensuit que Il s’ensuit que

Donc  > 1,1224. Les ventes du quatrième trimestre doivent progresser de 12,24 %

(ce qui ne sera pas évident à réaliser car les tondeuses de jardin se vendent très mal en automne).

Situation problème N° 2 :
Les ventes annuelles de tondeuses de jardin s’établissent ainsi :
	Année	2017	2018	2019
	Unités vendues.	600	750	690
1°) Quels sont les taux de croissance d’une année sur l’autre ? ( 2017 – 2018 ) ; (2018 – 2019 )
2°) Calculer le taux d’évolution global de deux façons différentes :
Corrigé :
1°)
De 2017 à 2018 on trouve le taux d’évolution positif :
Le taux d’évolution est donc de 25 %
( soit un coefficient directeur de 1,25 )
De 2018 à 2019 : on trouve :
Conclusion entre 2019 et 2018 on trouve une baisse de 8%
( ( Soit 1 – 0,08 = 0,92 ) soit un coefficient directeur de 0,92
2°) Calcule du d’évolution global de deux façons différentes : A et B
A ) La façon la plus simple de calculer l’évolution globale consiste à comparer 2017 et 2018. On calcule le taux de croissance entre 600 et 690 se calcule comme ci-dessus. On trouve 15 %.
B ) L’autre solution consiste à multiplier les coefficients directeurs des deux taux que nous venons de calculer. 1,25 × 0,92 = 1,15. Ce coefficient correspond bien à une hausse de 15 %.

Situation problème N° 3 : ( pour les filières ES)

Les ventes d'une entreprise augmentent deux années de suite de x %. Au total, la hausse s’élève à 21 %. Quelle est la progression annuelle ?

Corrigé 3 :

Il faut comme toujours raisonner avec les coefficients multiplicateurs.

Vente première année

Vente deuxième année :

= V2

+

+

+

L’expression ci- dessus est sous la forme

Se souvenir que 1² = 1

On nous donne :

V1 + V2 = 100 %+ 21 % soit 1 , 21

Se souvenir que

Après transformation

Donc   x = 0,1 × 100 = 10.

L’augmentation annuelle des ventes est de 10 %.

Situation problème N° 4 : ( avec les indices )
Les ventes sur six années se présentent comme suit :
	Année	2015	2016	2017	2018	2019	2020
	Unités vendues	500	520	480	600	750	690
Quelle est l’évolution relative observée entre 2015 et 2020 ? Calculer les indices de chaque année, base 100 en 2015. En déduire une remarque judicieuse.
Corrigé :
L’évolution sur les six années (soit cinq évolutions) se calcule comme dans les exercices précédents. On trouve facilement +38 %. Pour obtenir une série indicée 100 en 2018, il faut diviser toutes les valeurs par celle de 2015, c’est-à-dire 500, puis les multiplier par 100.
Soit 15%
La remarque à faire, c’est que l’augmentation de 38 % se constate aussi sur la dernière case du tableau (si l’on passe de 100 à 138, il est évident que l’augmentation est de 38 %).
Fin des exercices types : les refaire en auto-évaluation.

Travaux auto formatifs.

CONTROLE

Répondre aux questions suivantes :

1°) Quand dit – on que l’ Intérêt est simple ?

.

2°) Quand dit – on que l’ Intérêt est composé ?

.

3°) Qu’appelle – t –on « taux » ?

.

EVALUATION :

I ° Questions  :

A quel taux est placée une somme :

1°) De 400 € qui rapporte 200 € d’intérêt annuel .

2°) de 20 000 € qui rapporte 250 € en 3 mois ?

3°) de 20 000 € qui rapporte 1500 € en 3 ans?

II °) Exercices

a) A quel taux faut-il placer : 6950 € pour avoir un revenu de 278 € ?

b) 12000 € pour avoir 1140 € d’intérêt au bout de 2 ans ?

Situation problème N° 1 :

Un directeur commercial constate que ses ventes de nains de jardin ont augmenté de 12 % au premier trimestre, puis de 25 % au deuxième trimestre (par rapport au premier) et qu’elles ont diminué de 30 % au troisième trimestre. Quel devrait être la progression du quatrième trimestre pour dépasser l’objectif fixé pour l’année qui est de +10 % ? Arrondir à deux décimales

Situation problème N° 2 :
Les ventes annuelles de nains de jardin s’établissent ainsi :
	Année	2017	2018	2019
	Unités vendues.	600	750	690
Quels sont les taux de croissance d’une année sur l’autre ? Calculer le taux d’évolution global de deux façons différentes

Situation problème N° 3 : ( pour les filières ES)

Les ventes d'une entreprise augmentent deux années de suite de x %. Au total, la hausse s’élève à 21 %. Quelle est la progression annuelle ?

Situation problème N° 4 : ( avec les indices )
Les ventes sur six années se présentent comme suit :
	Année	2015	2016	2017	2018	2019	2020
	Unités vendues	500	520	480	600	750	690
Quelle est l’évolution relative observée entre 2015 et 2020 ? Calculer les indices de chaque année, base 100 en 2015. En déduire une remarque judicieuse.

Corrigé CONTROLE

Répondre aux questions suivantes :

1°) Quand dit – on que l’ Intérêt est simple ?

l’intérêt est dit : simple lorsqu’il ne s’ajoute pas au capital à la fin de chaque année , pour produire lui – même des intérêts .

2°) Quand dit – on que l’ Intérêt est composé ?

L’ Intérêt composé : l’intérêt est dit « composé » lorsqu’il s’ajoute chaque année au capital et produit des intérêts les années suivantes .

3°) Qu’appelle – t –on « taux » ?

Le taux est l’intérêt produit par une somme de cent € durant l’unité de temps qui a été stipulée .