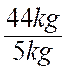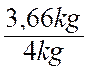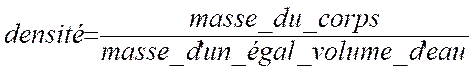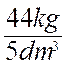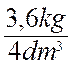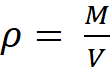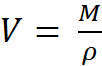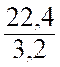Pré requis :
Activités pré requises : dossier 184
Lecture : Les anciennes unités
Système décimal
système métrique
Environnement du dossier
INDEX Warmaths (vers retour)			Objectif précédent 1°) Masse 2°) Volume d’un prisme			Objectif suivant : 1°)la pesée 2°) les unités de masse dans le système métrique			Tableau Vers la liste des cours de sciences…
DOSSIER : Définition ; présentation et calculs de la LA DENSITE et MASSE VOLUMIQUE (« r » ) ( « r » lire « rhô » ; voir alphabet grec )
	1°) Activités découvertes.
	2°) DENSITE . +INFORMATION 1 : Tableau des densités de matériaux courants nommés .
	3° ) MASSE VOLUMIQUE
	4°) Correspondance : « Masse volumique » et « densité ». +INFORMATIONS 2 : Masse volumique des principales essences de bois .
	5°) FORMULES en lien avec «  » ; « M » et « V »:
	6°) Travaux auto- formatifs. (cliquez ici)
TEST	COURS			Devoir Contrôle	Devoir évaluation			Série de situations problèmes :’Interdisciplinarité
				>>>>Devoir sommatif « classe »				Travaux niv !: VI et V Dos. 185
Les unités de poids							Les unités de masse
Devoir :							Devoir CC « poids et masse »

COURS
Activités découvertes :
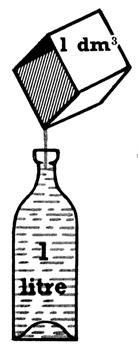
1°) Apporter une boîte de 1 décimètre cube et une bouteille de contenance d’un litre., verser le contenu du litre dans la boîte et vérifier que les deux mesure sont égales.
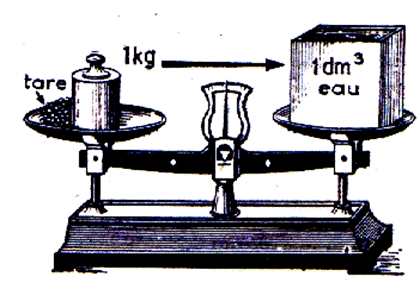
2°) Mettre le décimètre cube vide sur le plateau d’une balance , faire la tare , le remplir d’eau et constater que pour rétablir l’équilibre il faut mettre une masse de 1 kilogramme dans l’autre plateau et que par conséquent 1 kilogramme est le poids de 1 décimètre cube d’eau pure .
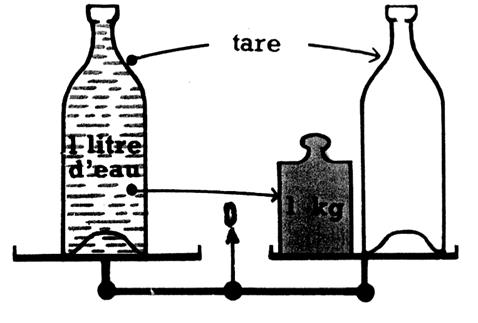
3 °) Etablir les égalités suivantes : 1 dm^3 = 1 litre = 1 kg d’eau pure On sait que : 1m^3 = 1 000 dm^3; On peut écrire : 1 m ^3 = 1000 litres = 1000 kg d’eau pure = 1 tonne.
ainsi que : 1 cm^3 = 1 millilitre = 1 gramme d’eau pure . 4°) Peser divers corps : Prendre des cubes de 1 décimètre de côté : de divers bois , ou contenant  des grains , de sable , de limaille de plomb , de fer , ….. et constater qu’à volume égal les corps ont des masses différentes ; On en tire de ces travaux la notion de « densité » .
2 ° ) DENSITE :
A ) Idée de la densité . Si l’on compare la masse des corps solides et liquides au masse d’un égal volume d’eau , on constate que les uns ( cuivre , fer , plomb , mercure , etc….) sont plus lourds ; plus denses que l’eau ; et que d’autres ( liège , huile , ….) sont moins lourds , moins denses que l’eau . Exemple I : expérience de mesure : 5 dm^3 de cuivre pèsent 44 kg ; 5 dm^3 d’eau ne pèsent que 5 kg Le cuivres pèse donc = 8,8 ; 8,8 fois plus que l’eau , ce qui s’exprime en disant que la densité du cuivre est 8,8 ( par rapport à l’eau) Expérience II : expérience de mesure : 4 litres d’huile pèsent 3,66 kg ; 4 litres d’eau pèsent 4 kg . l’huile pèse donc les = 0,915 , soit inférieur à 1 ; donc moins lourde que l’eau . La densité de l’huile est de 0 ,916.
B ) Définition :
On appelle « densité » d’un corps le quotient de la masse de ce corps par la masse d’un égal volume d’eau . Ce qui peut s ‘ écrire :  ;  La densité est un nombre abstrait ( elle n’a pas d’unité).
Activité n° 1 …
- 5 litres de chaux aérienne en poudre pèsent 2,5 kg - 5 litres d’eau pèsent 5 kg La densité de cette chaux est de = 0,5
Activité n° 2 …
- 5 dm ^3 de chaux aérienne en poudre pèsent 2,5 kg - 5 dm ^3 d’eau pèsent 5 kg La densité de cette chaux est de 2,5 5 = 0,5 Nota :Dans ce type de calcul , le volume est toujours exprimé dans la même unité.
INFORMATION 1 : Tableau des densités de matériaux courants nommés .

Liquides			Solides
Eau pure	1		Fer	7,90
Huile	0,90		Cuivre	8,80
Lait	1,03		Plomb	11,34
Pétrole	0,82		Argent	10,50
Essence	0,72		Or	19,27
Alcool	0,80		Platine	21,4
Mercure	13,59		Aluminium	2,70
			Bois de hêtre	0,85
			Chêne	0,93
Gaz :			Peuplier	0,40
Air		0,0013	Granit	2,60
			Marbre	2,70

3° ) MASSE VOLUMIQUE : (« r » lire « rô » lettre de l’alphabet grec )

On appelle « masse volumique » d’un corps , la masse de l’unité de volume de ce corps .

r =

· La masse volumique d’un corps est égale au rapport de sa masse sur son volume .( exprimée en Kg / m³ )

Nota : Parfois elle est exprimée en kg / dm ³

On dit aussi que la masse volumique est le quotient de la masse par le volume de ce corps .

L’unité est donc le kilogramme par mètre cube ou par décimètre cube :

Notée  : kg / m ³ ou kg .m^-3 et kg / dm ³ ou kg .dm^-3

Exemple : La masse volumique du mercure est de 13,6 kg . dm^-3 ou 13 600 kg . m ^-3

Exemples de calculs de recherche de la densité d’un matériau :

^- Masse volumique du cuivre = = 8,8 kg / dm³ ou 8800 kg / m³

^- Masse volumique de l’huile = = à, 915 kg / dm³ ou 915 kg /m³

4°) Correspondance : « Masse volumique » et « densité ».

Ø La masse volumique est exprimée généralement en kilogramme par mètre cube. Elle spécifie la masse en kilogramme d’un mètre cube de matière.

Ø La densité correspond au rapport entre la masse d’un volume de matière donnée et la masse d’un même volume d’eau .

La masse volumique exprimée en tonne ( 1000 kg) par mètre cube et la densité sont indiquées par le même nombre.

Exemples :

L’ Eau a pour densité « 1 » et a une masse volumique de de 1 t / m ³ ou de 1 000 kg / m³

Le mercure a pour densité « 13,59 » et il a une masse volumique de 13,59 t / m ³ ou de 13590 kg / m³

Le pétrole a pour densité « 0,82 » et il a une masse volumique de 0,82 t / m ³ ou de 820 kg / m³

INFORMATIONS 2 : Masse volumique des principales essences de bois :

Bois					(Suite ) Bois
Nom des essences			Masse volumique exprimée en Kg / m^3 et densité.		Nom des essences	Exprimée en Kg / m^3
Acacia			780 à 820  ; 0,78 à 0,82		Erable	560 à 840 ; 0,56 à 0,84
Acajou			560 à 850 ; 0,56 à 0,85		Frêne	840 ; 0,84
Aune			460 à 550 à 0,46 à 0,55		Gaïac	1339 ; 1,339 ;
Bouleau			520 à 730 à 0,52 à 0,73		Hêtre	800 ; 0,8
Buis de France			910 , 0,91		Hêtre ( 1 an coupe)	660 ; 0,66
Buis de Hollande			1320 ; 1,32		Liège	260 ; 0,26
Cèdre du Liban sec			490 ;		Mélèze	540 à 630 ; 0,54 à 0,63
Charme			759 à 900 ; 0,759 à 0,9		Orme	540 à 630 ; 0,54 à 063
Châtaignier			550 à 740 ; 0,55 à 0,74		Peuplier	390 ; 0,39
Chêne blanc			610 ; 0,61		Pin rouge	660 , 0,66
Chêne de démolition			730 ; 0,73		Pin du nord	740 ; 0,74
Chêne vert			983 ; 0,983		Platane	650 ; 0,65
Cœur de chêne (60 ans)			1170 ; 1,17		Poirier	700 à 840 , 0,7 à 0,84
Cormier			819		Pommier	730 à 800 ;
Ebène			1120 à 1200 ; 1,12 à 1,20		Sapin	450 ; 0,45
					Teck	860 ; 0,86
INFORMATIONS  3 : Tableau des masses volumiques de matériaux courants nommés
Liquides				Solides
				(revu et corrigé en 2013)
Eau pure	1000 kg / m^3			Fer			7900 kg / m^3
Huile	900 kg / m^3			Cuivre			8800 kg / m^3
Lait	1030 kg / m^3			Plomb			11340 kg / m^3
Pétrole	820 kg / m^3			Argent			10500 kg / m^3
Essence	720 kg / m^3			Or			19270 kg / m^3
Alcool	800 kg / m^3			Platine			21400 kg / m^3
Mercure	13590 kg / m^3			Aluminium			2700 kg / m^3
				Bois de hêtre			850 kg / m^3
				Chêne			930 kg / m^3
Gaz :				Peuplier			400 kg / m^3
Air		1,3 kg / m^3		Granit			2600 kg / m^3
				Marbre			2700 kg / m^3

4°) FORMULES en lien avec «  » ; « M » et « V »:

Si l’on désigne la densité d’un corps par la lettre « r » , son volume par la lettre « v » et sa masse par la lettre « m » :

La densité est égale au rapport de masse d’un corps par son volume :

d’où par transformation de l’égalité on peut écrire que

et

En tenant compte des unités correspondantes, on peut donc énoncer les règles suivantes ,sur les différents calculs possibles :

v 1^er type de calcul : La masse volumique d’un corps :

1°) la masse volumique d’un corps s’obtient en divisant sa masse par son volume .

(on dit aussi : que la masse volumique est égale au rapport de la masse de ce corps par son volume )

Application : une masse est égale à 18 kg et le volume à 7,5 dm³ , on a :

masse volumique r = = 2,4 kg / dm³

( 1 dm³ de ce matériau est équivalent à 2,4 dm³ d’eau )

v 2^ème type de calcul : La masse d’un corps

La masse d’un corps s’obtient en multipliant son volume par sa masse volumique .

Si le volume égale 25 cm³ et sa masse volumique est de 0,92 g / cm³ , on a :

Masse = 0,92 25 = 23 grammes

v 3^ème type de calcul : Le volume d’un corps

Le volume d’un corps s’obtient en divisant sa masse par sa masse volumique .

Si la masse égale 22,4 g et la masse volumique 3,2 g / cm³ , on a : Volume = = 7 cm³

Problèmes fait en cours  :

1°) Un cylindre a une masse de 2830 g . Quelle est sa masse volumique ?

Caractéristique du cylindre : R = 5 cm ; h = 2 dm ; pi = 3,14)

Solution : la masse volumique du cylindre est de : 1, 802547771

Résultat au gramme prés : 1,803 kg / dm³

2°) Un meuble (objet) de forme quelconque a une masse de 53,8 kg . La masse volumique de la matière qui constitue cet objet est : 0,610 kg / dm³ . Quel est le volume de bois utilisé ?

nota : on ne demande pas la forme ni les dimensions de l’objet

3° ) Un cube a 18 cm d’arête , il est fabriqué en teck ( masse volumique = 860 kg / m³) . Quelle sera la masse de ce cube .