Pré requis:

Notion de partage égale : Exemple : j’ai un paquet de bonbons qui contient 150 bonbons , je partage la totalité de ces bonbons entre 10 personnes , chacun recevra 15 bonbons .

J’ai donc 10 paquets de 15 bonbons . et , on dit que un paquet de 15 bonbons représente le dixième des 150 bonbons partagés .

Le mètre ( unité de longueur)

ENVIRONNEMENT du dossier:

Index

AVANT : La fraction décimale : diviser par 10

COURS

APRES :  2°) les sous multiples du mètre

Complément d’Info  : Décimètre – centimètre millimètre

La numération du nombre décimal: Découverte du « dixième »

Le dixième de mètre et le décimètre .

Travaux ; devoirs				Corrigé
TEST	Contrôle	évaluation comporte 2 parties à savoir faire !	Info :@	Contrôle	évaluation
			Ici fiche activités sur les dixièmes
			Les opérations sur les longueurs

COURS

Pour construire le décimètre on a partagé le mètre en 10 parties égales.

Le décimètre est contenu 10 fois dans le mètre .

On dit que :

Le décimètre est un dixième de mètre

Le décimètre est une fraction du mètre

Un décimètre ou dixième de mètre s’écrit de m

1 dm = de mètre

Exemple 1 :

Une planche mesure 3 m ;

la largeur est de 3 dixième de m .On écrit de m

Exemple 2 de calculs : additions de deux longueurs : 3 dm + 5 dm

1^er calcul : on sait que 3 dm + 5 dm = …8…dm

Puisque 3 dm = de m  et que 5 dm = de m ,

On remplace: 3 dm + 5 dm par de m + de m 

On obtient l’écriture :

Autre calcul : de m + de m  = 8 dm

Puisque 8 dm = de m  en conclusion on peut écrire que

de m + de m  est égal à de m 

A savoir : 1 m = 10 dm = de m

Se souvenir que 1 dm = 10 cm et donc =

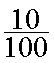
( nous avions vu : 1 dm = de m ; 10 cm = de m )

Vocabulaire :

Tout nombre entier « a » divisé par « 10 » , écrit : est appelée « fraction décimale » .

TRAVAUX AUTO FORMATIFS.

CONTROLE:

COMPLETER les phrases suivantes :

Pour construire le décimètre on a partagé le mètre en 10 parties égales.

Le décimètre est contenu 10 fois dans le mètre .

On dit que :

Le décimètre est un dixième de mètre

Le décimètre est une fraction du mètre

EVALUATION:

1°) on sait que de m = 3 dm

Traduire de même : de m = ….. ; de m = ….. ; de m = ….. ; de m = ….. ; de m = ….. ; de m = ….. ;

2°) on sait que 3 dm = de m

Traduire de même :

2 dm = de m ; 8 dm = de m ; 5 dm = de m ; 9 dm = de m ; 14 dm = de m ; 20 dm = de m ; 34 dm = de m ;

3°) A partir de la première égalité la compléter et la remplacer par des fractions.

Exercice 1

3 dm + 5 dm = ……dm , peut être remplacé par : de m + de m  = de m 

Exercice 2

4dm + 2 dm = ……dm

peut être remplacé par

de m + de m  = de m 

A savoir : 1 m = 10 dm = de m

4°) A partir de la première égalité la compléter et la remplacer par des nombres entiers

. exercice 1

de m + de m = de m

…..dm + …….dm = ……dm

exercice 2

de m + de m = de m ….. m

…..dm + …….dm = ……dm …..m

5°) A partir de la première égalité la compléter et la remplacer par des fractions.

Exercice 1

9 dm - 3 dm = ……dm

peut être remplacé par :

de m - de m  = de m 

Exercice 2

13 dm - 8 dm = ……dm

peut être remplacé par

de m + de m  = de m 

6°) A partir de la première égalité la compléter et la remplacer par des nombres entiers

. exercice 1

de m - de m = de m

…..dm - …….dm = ……dm

exercice 2

de m - de m = de m

…..dm + …….dm = ……dm

7°) . exercice 1

de m + de m = 1 m

exercice 2

de m - de m = 1 m

Partie 2 :

On sait que 1 dm = de m et que 10 cm = de m ;

Par ailleurs : 1 dm = 1cm donc de m = de m 

1°) Compléter :

4 dm = ……cm	19 dm = ……cm
de m = de m	de m = de m

2°) en suivant l’exercice ci-dessus :

8 dm = …..cm	35 dm =…………cm	5 dm = ………..cm
de m = de m	de m = de m	de m = de m

3°)

70 cm = ……..dm	50 cm = ……..dm	60 cm = ……..dm
de m =	de m =	de m =

4°)

290 cm = ……..dm	800 mm = ……….dm	90 cm = …………..dm
de m = de m	de m = de m	de m = de m

5°) on sait que 10 cm = 1 dm ; et que donc de m = 0,1 m

30 cm = ……..dm	80 cm = ………...dm	40 cm = ……….dm
de m = ………m	de m = …….. m	de m = ……. m

6°)

220 cm = ……..dm	150 cm = ………...dm	340 cm = ……….dm
de m = …2,2m	de m = …….. m	de m = ……. m

Exemple de transformation résolue :

5 dm + 45 cm = 50 cm + 45 cm = 95 cm = 0,95 m

de m + de m = de m +de m = de m = de m = 0,95m

S’inspirer de cet exemple pour faire le travail suivant :

7°)

2 dm + 7cm =	…cm+…..cm =	…………cm =	………..m
de m + de m	de m + de m	de m =	………..m

7 dm + 60cm =	…cm+…..cm =	…………cm =	………..m
de m + de m	de m + de m	de m =	………..m

80 cm + 7dm =	…cm+…..cm =	…………cm =	………..m
de m + de m	de m + de m	de m =	………..m