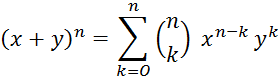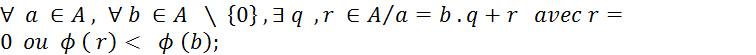Pré requis

Info : Voir cours sur les ensembles de nombres au collège et lycée..

ENVIRONNEMENT du dossier

INDEX « warmaths »

Objectif précédent : 1°)Le vecteur 2°) Calcul de la mesure algébrique d’un bipoint

Objectif suivant  vecteurs , espaces vectoriels , sous espaces vectoriels .

Info générales : Liste des cours sur le « repérage » Liste des cours sur les vecteurs.

DOSSIER les structures algébriques.

(voir le pré requis) Structures algébriques.

LES GROUPES , ANNEAUX , CORPS.

- A ) Groupes

- B ) Anneaux , sous anneaux , idéaux.

- C ) Anneaux particuliers , corps.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS sur les structures algébriques
Cours prérequis : « aux espaces vectoriels »
LES GROUPES , ANNEAUX , CORPS.
A) Groupes , sous-groupes. (voir :« groupe abélien »)
Définition : Une loi de composition interne (le signe est un point il représente n’importe quel signe identifiant une loi de composition interne : …….) «  » sur un ensemble « X » , est une application de
Voyons ce qu’est une loi de composition interne à un ensemble (appelée plus simplement OPÉRATION). Il s’agit d’une application qui peut être très simple, comme l’addition, l’inclusion ou la somme vectorielle, un peu plus sophistiquée, par exemple retirer d’un nombre une moyenne puis diviser le tout par un écart-type, ou carrément très compliquée. Comme il en existe une infinité, on se passera de leur recensement. Quelles propriétés peuvent avoir ces lois ? Notons deux lois non précisées avec T et *. Ces deux signes sont arbitraires (ne pas confondre l’étoile avec la touche « multiplier » d’un clavier). L’associativité : si (a T b) T c = a T (b T c). Il est évident que l’addition et la multiplication sont des lois associatives. Mais pas la division : (4 / 2) / 2 = 1 tandis que 4 / (2 / 2) = 4. Autre exemple, celui de la composition de fonctions : f o (g o h) = (f o g) o h. Voir aussi la page associativité du barycentre. La commutativité : il faut toujours que deux éléments soient permutables. On dit qu’ils « commutent ». Donc a T b = b T a. Parmi les opérations arithmétiques élémentaires, l’addition et la multiplication sont commutatives mais ni la soustraction ni la division n’ont ce privilège. L’élément neutre : c’est celui qui ne change rien. Par exemple 1 pour la multiplication et la division ou 0 pour l’addition ou la soustraction. Toute loi n’admet pas forcément un élément neutre. Un élément peut n’être neutre qu’à droite ou à gauche de l'élément auquel il s'applique. L’inversion : l’inverse d’un élément a est tel que si a T [inverse de a] = [inverse de a] T a = élément neutre. Par exemple 2 × ½ = ½ × 2 = 1. L’addition ne vérifie pas l’inversion dans tous les ensembles numériques puisqu’il faut un nombre négatif pour en inverser un positif. Voir aussi la page inversion d'une matrice. La distributivité entre deux lois : a T (b * c) = (a T b) * (a T c). La multiplication est distributive par rapport à l’addition (permettant développement et factorisation), l’intersection est distributive par rapport à l’union (et vice versa), etc. Il existe d’autres propriétés possibles comme l’identité ou l’absorption d’une loi par une autre…
Définition : 1. Un ensemble , ( lire : ensemble vide ) muni d’une loi de composition interne «  » est un groupe ,noté si : 1°) «  » est associative : , « (  » ; 2°) « G » contient un élément neutre pour «  » ,  ; 3°) Tout élément de « G » est inversible dans « G » : tel que . Si , de plus , la loi est commutative alors le groupe est commutatif ou parfois appelé « groupe abélien ».
Remarque : Un groupe est généralement noté additivement , ou multiplicativement . Dans le premier cas , il est commutatif et le symétrique est appelé « opposé » , tandis que dans le second cas il est appelé « inverse ». Info : Lecture des symboles : le symbole : lire « addition » ; le symbole : * lire « multiplication »
Définition : Une partie « H » d’un groupe « G » est un sous-groupe de « G » si la restriction à « H » de la loi « G » définit une structure de groupe.
Proposition 1 : Une partie non-vide « H » d’un groupe est un sous-groupe pour la loi   si : , ;
Proposition 2 : Les sous-groupes additifs du groupe additif sont les ensembles : où .
Exemples de groupes abéliens  : ( info + sur les ensembles de nombres ) ;  ;  ;  ;  ;  ; et ;  ; sont des groupes abéliens.
B – Anneaux , sous anneaux , idéaux.
Définition : Un anneau est un ensemble muni de deux opérateurs et appelé « addition » et « multiplication ». ( ;) est un groupe commutatif , la multiplication est associative , distributive par rapport à l’addition et elle possède un élément neutre .
Remarque : Pour nous , un anneau est nécessairement unitaire, il possède toujours un neutre pour la multiplication.
Exemples :
, ; , , , l’ensemble des polynômes à coefficients dans un anneau commutatif , sont des anneaux commutatifs.
Remarque :
l’ensemble des entiers relatifs pairs , ne sont pas des anneaux car n’est pas un groupe pour «  » et n’a pas d’élément neutre pour «   » .	N’a pas d’élément neutre
Proposition n°3 : Pour tout «  » permutables , et tout entier «  » positif ou nul , nous avons :
Sous anneaux.
Définition : La partie d’un anneau est appelée un sous-anneau de si : - est un sous -groupe additif de - est stable pour la multiplication. - Le neutre multiplicatif de appartient à
Exemples.
est un sous anneau de , de
Les polynômes de sans monôme du premier degré forment un sous anneau de
Les fonctions de forment un sous anneau de toutes les fonctions de
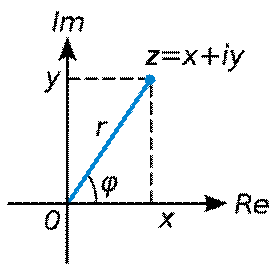
Rappel sur les nombres complexes :
Nombre complexe ( ensemble ) D’après un article de Wikipédia, l'encyclopédie libre. Représentation graphique du complexe x + iy = re^iφ à l'aide d'un vecteur. Mise en évidence de l'interprétation graphique de son module r et d'un de ses arguments φ. En mathématiques, les nombres complexes forment une extension de l'ensemble des nombres réels, contenant en particulier un nombre imaginaire (noté généralement i)^[^1] tel que i^2 = –1. Tout nombre complexe peut s'écrire sous la forme a + ib où a et b sont des réels. On peut munir l'ensemble des nombres complexes d'une addition et d'une multiplication qui en font un corps commutatif contenant le corps des nombres réels. Il est appelé corps des nombres complexes et se note ℂ. La notion de valeur absolue définie sur l'ensemble des nombres réels peut être étendue à l'ensemble des nombres complexes et prend alors le nom de module. Mais on ne peut pas munir l'ensemble des nombres complexes d'une relation d'ordre qui en ferait un corps totalement ordonné, c'est-à-dire qu'il n'est pas possible de comparer deux complexes en respectant les règles opératoires valables pour les nombres réels. Les nombres complexes furent introduits au 16 ^e siècle par les mathématiciens italiens Jérôme Cardan, Raphaël Bombelli, Nicolo Fontana, dit Tartaglia, et Ludovico Ferrari afin d'exprimer les solutions des équations du troisième degré en toute généralité par les formules de Cardan, en utilisant notamment des nombres de carré négatif, ainsi que les solutions des équations du quatrième degré (méthode de Ferrari). Ce n'est qu'à partir du 19^e siècle, sous l'impulsion de l'abbé Buée et de Jean-Robert Argand (plan d'Argand), puis avec les travaux de Gauss et de Cauchy, que se développe l'aspect géométrique des nombres complexes. On les associe à des vecteurs ou des points du plan. Les transformations du plan s'expriment alors sous forme de transformations complexes. En algèbre, le théorème de d'Alembert-Gauss énonce qu'un polynôme complexe non constant possède toujours au moins une racine complexe. Le corps des nombres complexes est dit algébriquement clos. On peut ainsi identifier le degré d'un polynôme complexe non nul au nombre de ses racines comptées avec leur ordre de multiplicité. En analyse, l'exponentielle complexe permet de simplifier l'étude des séries de Fourier, puis de définir la transformée de Fourier. La branche de l'analyse complexe concerne l'étude des fonctions dérivables au sens complexe, appelées fonctions holomorphes. En physique, les nombres complexes sont utilisés pour décrire le comportement d'oscillateurs électriques ou les phénomènes ondulatoires en électromagnétisme (Re(e^iωt) représentant une onde).
«  idéaux. »
Définition : Un idéal « I » d’un anneau est un sous groupe additif de vérifiant :
Exemples : Si est un anneau , et sont des idéaux de . Si est un anneau commutatif , l’ensemble des multiples d’un élément « b » , noté , est un idéal de .
Définition : Un idéal d’un anneau commutatif est dit principal s’il existe
C ) ANNEAUX PARTICULIERS , CORPS.
Définition : Un élément non nul « a » de est un diviseur de zéro à droite ( resp. à gauche ) s’ il existe un élément « b » de non nul tel que ( resp .. Nous disons que c’est un diviseur de zéro si c’est un diviseur de zéro à droite ou un diviseur de zéro à gauche.
Définition : Un anneau intègre est un anneau différent de l’anneau nul , réduit à , commutatif et sans diviseur de zéro , c’ est à dire :
Définition : Un élément de «  » de est dit « nilpotent » lorsqu’il existe un entier tel que . Le plus petit entier pour lequel cette identifié est vérifiée est appelé l’ordre de nilpotence de «  ».
Définition : Un anneau est principal s’il est intègre et que tous ses idéaux sont principaux .
Exemple : sont principaux . ne l’est pas .
Définition : Si est un anneau intègre pour lequel pour lequel il existe une application ( phi)  : appelée stathme euclidien sur , vérifiant les deux propriétés : · ( voir le division euclidienne) ·
Proposition 4 . Un anneau euclidien est principal. Exemples : muni de la valeur absolue , et munis du degré sont euclidiens.
Définition : Un corps est un anneau dans lequel l’ensemble des éléments non nuls , , est un groupe pour la multiplication , c’est-à-dire un anneau , non réduit à , pour lequel tout élément non nul a un inverse pour la multiplication.
Exemples : pour « p » un nombre premier , sont des corps commutatifs.
FIN DE CE COURS …. Suite voir : vecteurs , espaces vectoriels , sous espaces vectoriels .

TRAVAUX AUTO FORMATIFS.

CONTROLE : Apprendre les définitions du cours …

Evaluation . Voir les propositions et exemples.