Pré requis:
ENVIRONNEMENT du dossier:
DOSSIER : LE PRODUIT SCALAIRE de deux vecteurs.
|
TEST

|
COURS

|
Devoir Contrôle 
|
Devoir évaluation 
|
Inter
disciplinaire 
|
|
Corrigé Contrôle 
|
Corrigé évaluation 
|
Ce cours est la présentation
d’u outil mathématique utilisé en physique : exemple Sciences : le travail d’une force
COURS
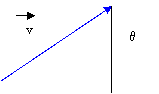
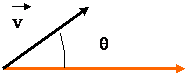
1°) Angle de deux vecteurs. :
On
appelle angle de deux vecteurs le secteur
angulaire saillant obtenu en menant par un point arbitraire les demi-droites parallèles à ces vecteurs et de même sens.
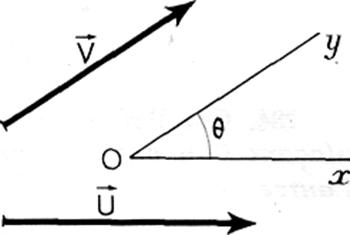
L'angle des vecteurs U et V
(flg. 184) est l'angle saillant zOy
= 9, compris entre 0 et deux droits, obtenu en menant par un
point arbitraire O du plan les demi-
droites Ox
et Oy respectivement parallèles aux
vecteurs U et V, et de même sens. On sait que l'angle obtenu
est indépendant du sommet choisi O.
2°) Définition du produit
scalaire de deux vecteurs. :
Le
produit scalaire de deux
vecteurs est le nombre relatif égal au produit de leurs modules par le cosinus de leur angle.
|
Soient
| 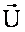 | = u
; | | = u
; |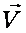 | = y les
modules (ou longueurs) | = y les
modules (ou longueurs)
des
vecteurs U et V et 6 leur angle (flg. 184). Leur
produit
scalaire se représente par le symbole : U . V
(lire 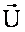 scalaire scalaire 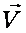 ) et : ) et :
|
|
 Calcul
de la norme du vecteur : v’ :
(projection du vecteur v sur
la droite « D » )
Calcul
de la norme du vecteur : v’ :
(projection du vecteur v sur
la droite « D » )
|| v’|| = ||
v || cos q
« v’ » est la
projection de « v » sur la droite « D »


 Le produit scalaire deux
vecteurs ( u et v )
est égal au produit de la norme
du premier vecteur ( noté : ||
u || )
par la projection de
Le produit scalaire deux
vecteurs ( u et v )
est égal au produit de la norme
du premier vecteur ( noté : ||
u || )
par la projection de
la norme du second
vecteur ( v ) .( noté || v’|| )
Le produit scalaire
des vecteurs u et
v ( noté :
u . v )
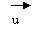
*remarque :

 « Cosinus
téta » se note : « cos q » ou « cos
( u ,
v ) »
« Cosinus
téta » se note : « cos q » ou « cos
( u ,
v ) »
relation mathématique du produit scalaire
de deux vecteurs :
u . v =
|| u || 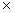 || v ||
|| v ||
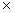 cos q
cos q

 avec : l’angle q
= l’angle (
u , v
)
avec : l’angle q
= l’angle (
u , v
)
Travaux auto formatifs.
Contrôle
Traduire : 



u . v =
|| u || 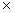 || v ||
|| v ||
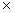 cos q
cos q

 avec : l’angle q
= l’angle (
u , v
)
avec : l’angle q
= l’angle (
u , v
)
EVALUATION:
Interdisciplinarité :
|
Géométrie : Relations métriques dans le
triangle quelconque .
|

|
|
Sciences : le travail d’une force
|

|