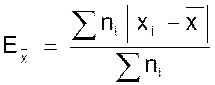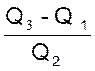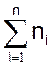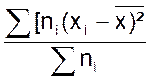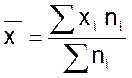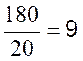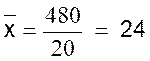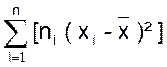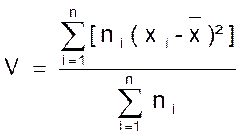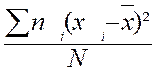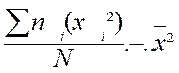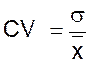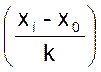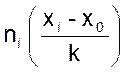Rappel :

I )  Les caractéristiques de position  sont : le mode ; la médiane ; les quartiles et les moyennes .

A savoir :
 Les  caractéristiques de dispersion sont  :

·       L’ étendue ,

·       L’ intervalle interquartile ,

·       L’ intervalle interquartile relatif ,

·       L’ écart moyen arithmétique ;

·       La variance et l’ écart type .,

COURS

1°) Etendue :

Vu

en 3^ème

L’étendue  d’une série statistique est la différence entre la plus grande valeur «  x _M » ,et la plus petite valeur «  x _m » du caractère ( voir population).

Exemples

-       on a mesuré des longueurs de 50 barres : la plus petite longueur est 541 mm ; la plus longue est 562 mm : l’étendue est de 562 – 541 = 21 mm .

-       On a mesuré des masses  d’une série de pièces de fonderie ; la plus lourde est de 115 kg ; la plus petite est de 98 kg ; l’étendu est de 115 – 98 = 17 kg.

-       On a mesuré des personnes pour la taille ;la plus grande mesure 2,05 m ; la plus petite 1 ;69 m : l’étendue est de 36 cm.

e  =  x _M  - x _m

où :   « e » : étendue  , «  x _M » : plus grande valeur du caractère ; «  x _m » : plus petite valeur du caractère 

Application :

Caractères :x _i

Effectifs : n_i

17

1

Calcul de l’étendue :

19

1

  e = 31 - 17  =  14

21

2

23

6

Calcul de la somme des effectifs :

( notée :  )

= 1 + 1 + 2 + 6 + 5 + 3 + 2 + 0 = 20

25

5

27

3

29

2

31

0

20 

En résumé :

La première caractéristique de dispersion est « l’étendue »

Ce paramètre est également appelé « intervalle de variation ». Cette caractéristique est la plus simple  mais aussi la moins significative .

Par définition : l ‘ « étendue »  ( e ) d’une série statistique est la différence entre la plus grand valeur et la plus petite valeur du caractère.

Calcul : si  « x _M »   est la plus grande valeur  et  « x _m » la plus petite valeur alors on calculera :  

e =  x _M   -   x _m  

Autre exemple : soit la série statistique suivante :

x _i

Fréquences  ( f _i )

100

2

105

15

110

29

115

16

120

3

65

L’étendue est de   120 - 100 = 20

Commentaires :Ce calcul est simple mais  la simplicité de ce calcul ne doit pas nous faire oublier que « l’ étendue » est très sensible aux  fluctuations des valeurs « extrêmes » qui sont souvent peu représentatives.

Cette valeur caractéristique, qui correspond à un concept fort utilisé dans la pratique ( écart entre le premier et le dernier coureur , écart entre la meilleur et la plus faible note, etc.) est insuffisante pour une étude sérieuse de la dispersion.

2°) La variance

CALCUL de la variance :   ( pré requis : la moyenne  arithmétique :   ) :

► Notion de variance :

Exemple : considérons la notation par 2 professeurs qui ont la même moyenne mais des notes extrêmement différentes : l’un note de 2 à 18  , alors que l’autre note de 8 à 14 . il se peut que le calcul de la moyenne des notes de chacun d’eux soit la même. Il faut un autre indicateur.

La « variance » est égale à  la « somme des carrés des écarts »

Un écart est égal à la différence d’une note d’un élève avec la note moyenne (calculée).. 

► La variance est un indice de dispersion.

►On désigne la variance  d’une série statistique par la lettre  « V ».

► La variance d’une série statistique est la moyenne arithmétique des carrés des écarts :   ( x _i  -   ) ²  

soit la formule :  V =

Exemple de calculs :

Les données sont :

Calcul des

Calcul  de la

moyenne

Calcul des

Calcul des

Calcul des

Calcul de la

 Variance :V

x _i

n_i

     x _i n_i

( x_i - )

( x_i - )²

n_i( x_i - )²

17

1

  17

17 -24 =   - 7

49

49

V =

formule : V =

   V =     9

19

1

  19

19 -24  =  - 5

25

25

21

2

  42

21 - 24 =   - 3

9

18

23

6

138

23 - 24 =   - 1

1

6

25

5

125

25-24 =    +1

1

5

27

3

  81

27 - 24 =   +3

9

27

29

2

  58

29 - 24 =  + 5

25

50

31

0

   0

31 - 24 =  + 7

49

0

Calcul de

                      = 20

Calcul de = N

      =  480

total

180

Résumé :  Procédure à respecter pour calculer la variance (notée par la lettre abrégée :  V )

Pour calculer la variance on fera dans l’ordre : (nota :pour simplifier l’organisation des résultats on préférera toujours le tableau numérique)

1°) Calcul de la somme des effectifs  =  N  

2°) calcul des  produits   « x _i n_i »

3°) Calcul de la somme des  produits   « x _i n_i»  notée :  

4°) Calcul de la moyenne arithmétique « pondérée » par les effectifs : 

5° ) Calcul des écarts  ( x_i - )    ( écart compris entre la valeur du caractère et la valeur moyenne)

6°) Calcul des carrées des écarts :   ( x_i - )²

7°) calcul des produits de  carrés des écarts par les nombres correspondant  des effectifs par caractère . On dit aussi :  Pondération des carrés des écarts par les nombres correspondants de s effectifs.( le calcul ( x_i - )²  par le « n_i » est dit  «  pondéré »)

8°) Calculer la somme des carrés des écarts « pondérés » précédents :

9°) Calcul de la variance : la valeur de la variance est  égale au rapport de la somme des carrés des écarts « pondérés » par la somme des effectifs.

Remarque : lorsque la moyenne arithmétique est une valeur entière, les calculs sont relativement simples, mais la plupart du temps  est un nombre décimal, ce qui rend l’élévation « au carré » des écarts plus difficile. Il est alors conseillé d’utiliser la calculatrice  pour éliminer cette difficulté.

FORMULES : ( pouvant être  utilisées  pour calculer la  variance)

V = 

Autres formules :       V = 

ou   V =

3°) Ecart type :  ( symbole : «  »)

         On appelle « écart type » d’une série statistique la racine carré de sa variance :         

L’écart type  noté (sigma :  s ) permet de caractériser la dispersion des valeurs d’une série par rapport à la moyenne.

Son intérêt :

Il permet de :

1) Soit comparer la dispersion de plusieurs séries qui ont la même moyenne. A ce propos : plus l’écart type est grand  , plus la série a des variables dispersées autour de la moyenne.

2) Soit de savoir combien de variables  se trouvent dans un intervalle centré sur la moyenne et d’amplitude  s  ou 2 s , par exemple .

Suite de l’exemple précédent :

On a calculé la variance : V = 9

L’écart type =     = 3 

Conclusion :

Propriétés  et commentaires :

A ) l’ écart type.

L’écart type indique comment , en moyenne, les valeurs de la variable sont groupées autour de la tendance centrale. Une série statistique dont l’écart type est faible est une série où les valeurs sont peu dispersées on peut dire que la série statistique  est alors homogène. Inversement , un écart type important est représentatif d’une série très dispersée.

Ainsi l’écart type permet d’apprécier le « risque » d’une valeur de la variable, prise au hasard, soit proche ou éloignée (en valeur positive ou valeur négative) de la moyenne.

Exemple simple permettant de saisir la signification de l’écart type :

Deux compagnies aériennes concurrentes  X et Y assurent , entre les deux villes A et B , des vols réguliers ( Départ de  A = 9 h)

L’étude de la durée des vols a permis d’établir , pour les deux compagnies, les caractéristiques   et s  suivantes :

Pour X : ( 6 h ;  )   Et pour  Y   ( 6 h ;  )

Ces caractéristiques indiquent qu’il faut, en moyenne, 6 heures pour se rendre de la ville A à la ville B, quelque soit la compagnie choisie, mais que les vols ont une durée plus irrégulières avec la compagnie Y ( écart type le plus élevé : 15 min) qu’avec la compagnie X ( 6 min).

Supposons qu’un homme d’affaires désire se rendre dans la ville B pour un rendez -vous fixé à l’aéroport de B à 15 h 15 min. Il y a fortes chances d’être à l’heure, s’il voyage par la compagnie X ( il est vraisemblable que la durée du vol sera comprise entre 5 h 54  ( 6 h - 6 min )  et 6 h 6 min  ( 6h + 6 min). Par contre , si le rendez vous est à 14 h 45 min , l’homme d’affaires à quelques chances d’être à l’heure par la compagnie Y , parce qu’il se peut que le vol ne dure que 5 h 45 ( 6 h - 15 min)

B )  Le coefficient de variation :

Défini seulement pour des variables positives , le coefficient de variation facilite les comparaisons, car il est une valeur « sans dimension », indépendante des unités de mesure « x _i » :

Son expression  est la suivante :  

Tableau statistique d’une production en série de pièces usinées.

(commentaire 1: dans un travail en série , la côte d’usinage varie pour différentes raisons , notamment parce que les pièces ne sont pas toujours dans la même  position , parce que l’outil qui retire de la matière s’use dans le temps ;… ; pour ces raisons il est souvent  décidé que dans une fabrication en série  on effectuera des prélèvements statistiques  toutes les « x » pièces ; dans l’exercice suivant l’étude porte sur 100 pièces prélevées et mesurées ;

(commentaire2 : dans l’atelier de fabrication , après études des résultats statistiques des lots de  pièces hors côte sont mises à la réforme , une intervention s’avère nécessaire pour refaire les réglages de machine ou affûtage d’outils .) 

En conclusion :   EXEMPLE RECAPITULATIF

Avec cet exemple , nous allons calculer l’ensemble des caractéristiques qui permettent d’analyser une série statistique.

1°) On demande de calculer les caractéristiques de tendance centrale et de position :

·       Mode ;

·       Médiane ;

·       Quartiles ;

·       moyenne arithmétique.

2°) On demande de calculer les  caractéristiques de dispersion :

·       étendue ,

·       intervalle interquartile ,

·       intervalle interquartile relatif ,

·       écart moyen arithmétique ;

·        écart type .,

Les données sont :

Soit le tableau ci après relatif à la distribution de supports informatiques inscriptibles  ( C.D ; et D.V.D et cassettes ) vendus par une entreprise de diffusion par correspondance, en fonction de leur prix.

Classes de prix.

x _i

n _i

ECC

] 160 à 170]

165

150

] 170 à 180]

175

190

] 180 à 190 ]

185

203

] 190 à 200 ]

195

270

] 200 à 210 ]

205

190

] 210 à 220]

215

150

] 220 à 230]

225

105

CONTROLE :

A venir

EVALUATION

A venir

CORRIGER DE L’EXEMPLE RECAPITULATIF.

Les données sont :

Soit le tableau ci après relatif à la distribution de supports informatiques inscriptibles  ( C.D ; et D.V.D et cassettes ) vendus par une entreprise de diffusion par correspondance, en fonction de leur prix.

Classes de prix.

x _i

n _i

ECC

] 160 à 170]

165

150

150

-3

- 450

] 170 à 180]

175

190

340

-2

- 380

] 180 à 190 ]

185

203

543

-1

- 203

] 190 à 200 ]

195

270

813

0

0

] 200 à 210 ]

205

190

1 003

+1

+  190

] 210 à 220]

215

150

1 153

+2

+ 300

] 220 à 230]

225

105

1 258

+3

+ 315

=

1 258

-  1 033

+ 80 5

( - 1033) + ( + 805) = ( - 228)

1°) Les caractéristiques de tendance centrale et de position :

Mode : Classe modale « 190 à 200 ». On peut prendre comme mode la valeur 195

Médiane :

Ici SUITE DU CORRIGE.