Pré requis:


ENVIRONNEMENT du dossier:
Index		Objectif précédent :			Objectif suivant :			tableau .
DOSSIER : THEORIE DES COMBINAISONS. · Les questions qu’on peut se proposer en général sur la théorie des combinaisons sont fort intéressantes : Elles révèlent l’immoralité des jeux de hasard, et d’expliquer les déceptions qui trop souvent sont au bout des spéculations humaines. Chapitres : - « arrangements » - « permutation » - « combinaisons » - Théorie des combinaisons. Et Exemples.
TEST	COURS		Devoir Contrôle	Devoir évaluation		Interdisciplinarité	Corrigé Contrôle		Corrigé évaluation

Exemples de pb :

· De combien de manières différentes huit personnes peuvent-elles se placer autour d’une table ?

· Calculer le nombre des permutations qu’on peut faire avec 24 lettres ?

· On a 90 numéros dans une urne , et l’on en tire 1 , ou 2 , ou 3 ou 4 , ou 5 ; ou 6 , quelle chance a-t-on que les numéros sortants soient ceux qu’on aurait désignés d’avance ?

· On doit loger 40 personnes dans deux dortoirs différents : le premier contient 33 lits , le second 7 lits ; de combien de manières peut-on distribuer ces 40 personnes. ?

· Au jeu de boston on donne 13 cartes sur 52 , combien de combinaisons différentes ?

· Calculer le nombre de coups différents que l’on peut amener au jeu de dés .

· Quelle est la probabilité que tous les dés marquent le même point ? .

· Quelle est la probabilité d’amener trois points égaux avec quatre dés ?

COURS

A) Lorsque divers objets sont réunis dans un même lieu, tels que des personnes dans une salle, des numéros dans un sac, des cartes sur une table, il est intéressant de pouvoir .se rendre compte des résultats variés qu’on obtiendrait en groupant ces objets de toutes les manières possibles. Pour étudier ces chances (possibilités) il faut fixer la valeur de certaines expressions.

B) « Arrangement » Quand on prend ces objets indistinctement, et qu’on les groupes par 2 , par 3, par 4, etc.………par « n » ,on dit que l’on forme des arrangements 2 à 2 , 3 à 3 , 4 à 4, « n » à « n » ….

C) « Permutation » Si, dans un de ces groupes,ou dans tous les objets ou personnes réunis,on opère tous les déplacements possibles,en faisant parcourir à chaque objet ou personne toutes les phases intermédiaires,on obtient ce que l’on appelle des « permutations ».

D) « Combinaison » Enfin, quand on a formé tous les arrangements 2 à 2 ,3 à 3, 4 à 4 , « n » à « n » , si l’on ne prend que ceux qui différent entre eux par un objet ou personne au moins, ces arrangements prennent alors le nom de « combinaisons » 2 à 2 , 3 à 3 , 4 à 4 , « n » à « n » .

Exemple :

Prenons , par exemple, les 25 premières lettres de l’alphabet, et proposons nous de déterminer tous les arrangements (1) , toutes les permutations (2), toutes les combinaisons (3) dont les lettres sont susceptibles , et d’en calculer le nombre.

(1) Arrangements.

Arrangement 2 à 2

Après avoir écrit sur une même ligne les lettres : a,b,c, d, e, ……………………………………………………………………………………………………………………,y ,

Si l’on prend le première lettre « a » et que l’on écrive alternativement à la suite chacune des 24 autres lettres, on formera ( 25 -1) soit 24 arrangements 2 à 2 commençant par la lettre « a » comme on peut le voir :

ab, ac ,ad, ae , ……………………………………………………………………………………..ax, ay.

De même ,si , à la suite de la lettre “b” ,on écrit successivement chacune des 24 autres, on aura 24 arrangements 2 à 2 , commençant par « b » .

ba, bc, bd, ……………………………………………………………………………………………………………..by

Enfin, la même opération, appliquée à chacune des lettres de l’alphabet, donnera 25 séries de 24 arrangements de 2 à 2 , ou bien 25 X 24 = 600 arrangements 2 à 2..

C'est-à-dire qu’en général si « m » désigne le nombre d’objets ou personnes donnés « m ( m-1) » sera le nombre de tous les arrangements 2 à 2 dont ces objets ou personnes sont susceptibles.,

A la suite d’arrangement 2 à 2 , on écrit successivement chacune des 23 lettres restantes , on formera les arrangement 3 à 3 .

« abc , abd, abe, abf,…………………………………………………………………… ;aby »

“acb, acd, ace, acf ,……………………………………………………………………..;acy“

“bac, bad,bae,baf,........................................................................................,bay”

“bca,bcd,bce,bcf,...........................................................................................bcy”

etc. ………………………………………………………………………………………….

et comme chaque arrangement 2 à 2 donnera 23 arrangements 3 à 3 , nous aurons en tout 25 X 24 X 23 = 13 800 arrangements 3 à 3 , c’est à dire qu’en généralisant “m” objets ou personnes sont susceptibles d’un nombre d’arrangements 3 à 3 correspondant à « ( m -1) ( m – 2) .

arrangement 4 à 4 :

De même pour former les arrangement 4 à 4 ,il faudra écrire à la suite de chaque arrangement de trois lettres chacune des lettres restantes ; en sorte que « m ( m-1)(m-2)(m-3) exprimera le total des arrangement 4 à 4 et ainsi de suite………………

En général :…………………………

Le raisonnement précédent nous fait comprendre à la fois comment on forme tous les arrangements et comment on en calcule le nombre. Donc ,en général :

« m ( m-1) » ……………………………………………… donne le nombre des arrangements 2 à 2,

« m ( m-1) ( m – 2) » ……………………………… donne le nombre des arrangements 3 à 3,

« m ( m-1) ( m – 2) ( m -3 ) » ……………………………… donne le nombre des arrangements 4 à 4,

………………………………..

« m ( m-1) ( m – 2) ( m -3 ) ………………………( m – 9) » ……………………………… donne le nombre des arrangements 10 à 10

…………………………………..

« m ( m-1) ( m – 2) ( m -3 ) » ………………( m – ( n-1) ) … donne le nombre des arrangements n à n,

C'est-à-dire que pour avoir le nombre de tous les arrangements « n à n » que l’on peut former avec « m » objets ou personnes donnés , il faur faire le produit de tous les nombres entiers consécutifs depuis « m » jusqu’à « m – ( n-1) » ou « m – n + 1 » ,ou bien jusqu’au facteur qu’on obtient en diminuant « m » d’une unité de moins qu’il y a d’objets ou de personne dans chaque groupe.

Permutations :

Avec 2 lettres (objets, personnes,….):

Quand on a deux lettres « a » et « b » ,on peut les placer de deux manières différentes :

« ab » et « ba » ,

ce qui donne deux permutations.

Avec 3 lettres :

Si l’on a trois lettres « a », »b », »c » et qu’on voulu former les permutations dont elles sont susceptibles,il faudrait introduire la 3^ème lettre « c » dans chacune des permutations des deux autres,en lui faisant occuper successivement toutes les places possibles ,comme on le voit ci –après ; ainsi :

« ab » donne « abc , acb,, cab »

« ba » donne « bac, bca , cba »

ce qui fournit 2X3 = 6 permutations.

Avec 4 lettres (objets, personnes,….):

Les permutations de quatre lettres « a,b, c, d » s’obtiendront en faisant parcourir à la quatrième lettre « d » toutes les places possibles dans chacune des permutations des trois autres,ce qui donnera quatre permutations de 4 lettres pour chaque permutations de trois lettres. En effet :

« a,b,c » donne « a,b,c,d » « a,b,d,c » « a,d, b,c » «d, a,b,c »

« a,c,b » donne “a,c,b,d » “a,c,d,b » “a,d,c,b » “d,a,c,b »

etc........................................................

Complétrer:

« cab » donne ……………………………………..

« bac » donne …………………………………………..

«bca » donne …………………………………………

« cba » donne…………………………………………

C'est-à-dire qu’en tout nous aurons :

2 X 3 X 4 = 24 permutations pour 4 permutations…………. ;

Si nous continuons ainsi , nous trouverons que le nombre des permutations de 5 lettres s’obtient en multipliant par 5 le nombre des permutaions de 4 lettres et ainsi de suite, On a donc en général :

1 X 2 pour le nombre des permutations de 2 objets.

1 X 2 X 3 pour le nombre des permutations de 3 objets.

1 X 2 X 3 X 4 pour le nombre des permutations de 4 objets.

1 X 2 X 3 X 4 X 5 pour le nombre des permutations de 5 objets. ( soit 120 permutations possibles)

………………………………………………………………………………………..

1 X 2 X 3 X 4 X 5 X…………………………………………….X « n » ; pour le nombre des permutations de « n » objets.

Combinaisons.

· Pour trouver les combinaisons 2 à 2 ; 3 à 3 ; 4 à 4 , ………..etc.………..d’un certains nombres d’objets (cartes, boules,……………) ,il faut employer un moyen analogue à celui indiqué pour les arrangements ;(voir ci-dessus) , mais avec la modification suivante :

On prend d’abord la première lettre (objet…) « a » ,et, comme ci-dessus,on écrit, alternativement à sa suite les autres lettres (objets) de l’alphabet,

ce qui donne :

« ab , ac, ad , ae, ……………………………………………………………………………………………….,az »

ensuite on prend la seconde lettre “b”, et l’on écrit successivement , après elle celles qui la suivent , en posant :

« , bc, bd , be, bf ……………………………………………………………………………………………….,bz »

de même , la 3ème lettre “c” avec les suivantes, en les associant une à une , donne :

« cd , ce, cf , cg, ……………………………………………………………………………………………….,cz »

et ainsi de suite,sans revenir en arrière, ce qui fournira un nombre de combinaisons 2 à 2 moitié moindre que celui des arrangements 2 à 2 des mêmes lettres, c'est-à-dire ,

si « m » désigne le nombre d’objets , le nombre de combinaisons sera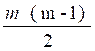

Exemple de problème : soit 6 objets de même nature , calculez le nombre de combinaisons 2 à 2 possibles :

Réponse : 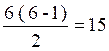combinaisons 2 à 2 possibles………….

Combinaisons 3 à 3 :

· Pour les combinaisons 3 à 3 , il faut prendre chacune des combinaisons 2 à 2 , et écrire alternativement à sa suite chacune des lettres qui , dans l’ordre alphabétique , suivent la dernière lettre de cette combinaison 2 à 2, ainsi les combinaisons ci-dessus donneront pour les combinaisons 3 à 3 ,

Pour les combinaisons 3 à 3 , il faut prendre chacune des combinaisons 2 à 2 (voir ci-dessus) , et écrire alternativement à sa suite chacune des lettres qui , dans l’ordre alphabétique ( ou fixé) , suivent la dernière des lettres de cette combinaison 2 à 2 , ainsi les combinaisons ci-dessus donneront pour les combinaisons 3 à 3 ,

« abc , abd , abe , abf, ……………………………………………………………………………………………….,abz »

« acd , ace , acf , acg, ……………………………………………………………………………………………….,acz »

« ade , adf , adg , adh, ……………………………………………………………………………………………….,adz »

...................................................................................................................................................................

« bcd , bce , bcf , bcg, ……………………………………………………………………………………………….,bcz »

« bde , bdf , bdg , bdh, ……………………………………………………………………………………………….,bdz »

…………………………………………………………………………………………………………………………………………….

« cde , cdf , cdg , cdh, ……………………………………………………………………………………………….,cdz »

etc………………………………………………………………………………………………………………………………………

Pour évaluer le nombre de ces combinaisons 3 à 3 ,il faut observer d’un côté que ces combinaisons doivent différer toutes par une lettre au moins,et de l’autre qu’un groupe de trois lettres, « abc »par exemple,donne six permutations. (voir ci-dessus)

« abc, acb, cab, bac, bca, cba »

Ainsi donc , une seule de ces permutations doit figurer parmi les combinaisons ci-dessus, tandis qu’elles font toutes partie des arrangements 3 à3 (ci-dessus), Par cons équent, le nombre des combinaisons 3 à 3 est six fois moindre que celui des arrangements 3 à 3 , on aura donc :

Pour le nombre de combinaisons de « m » objets pris 3 à 3 :

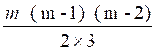
Exercice : au départ d’une course de chevaux ( 15) combien de chances a-t- on pour trouver les trois chevaux placés dans les trois première places.( soit dans le désordre et ordre compris) ?

· Les combinaisons 3 à 3 étant connues, si l’on écrit successivement à la suite de chacune d’elles les lettres qui suivent la dernière, on obtiendra les combinaisons 4 à 4 , quant à leur nombre, nous prouverons, par un raisonnement analogue au précédent, qu’il doit être 24 fois moindre que celui des arrangements 4 à 4 ( voir ci-dessus) , que l’on peut exprimer par l’expression :

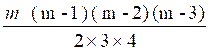; « m » représentant le nombre d’objets.

· Généralisons :

Donc, en général, le nombre des combinaisons s’obtient en divisant le nombre des arrangements par celui des permutations , c'est-à-dire que la formule générale des combinaisons de « m » objets groupés « n à n » est :

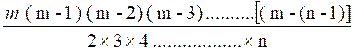
· Pour résumer toutes les considérations précédentes , nous dirons que,si les lettres employées étaient des facteurs premiers , les mots « arrangements », »combinaisons » , « permutations » auraient les significations suivantes :

1°) les arrangements 2 à 2 , 3 à 3 ,………………………………………………. n à n représentent tous les procédés qu’on peut mettre en usage pour former avec ces facteurs , des produits 2 à 2 , 3 à 3 , …….n à n , en les prenant successivement dans tous les ordres possibles.

2°) Les combinaisons 2 à 2 , 3 à 3 ……………………………………….n à n sont tous les produits différents que l’on peut obtenir en multipliant ces facteurs 2 à 2 , 3 à 3 ……………………………………….n à n.

3°) Les permutations ne donnent qu’un seul produit, puisque tous les facteurs entrent à la fois dans chaque groupe ; mais elles indiquent toutes les manières dont ce produit peut être effectué .

· Exemple : c’est ainsi , par exemple, que si le capitaine d’une compagnie veut disposer ses soldats sur DEUX , trois, quatre colonnes, etc. ……, d’après tous les modes possibles,il formera des arrangements 2 à 2 , 3 à 3 , 4 à 4 ,etc…………………… ;

Que ‘il veut prendre , au hasard, 2 ; 3 ; 4 hommes, etc..,pour une expédition, il aura à choisir sur les combinaisons 2 à 2 ; 3 à 3 ; 4 à 4 ;etc….

Qu’enfin, si ce capitaine réunit sa troupe en cercle autour de lui ou sur une seule file,en laissant à chaque soldat la faculté d’occuper tour à tour toutes les places possibles, la compagnie exécutera des permutations.

Théorie des combinaisons.

· Les questions qu’on peut se proposer en général sur la théorie des combinaisons sont fort intéressantes : Elles révèlent l’immoralité des jeux de hasard, et d’expliquer les déceptions qui trop souvent sont au bout des spéculations humaines.

Toutes ces questions sont résolues par les trois formules générales trouvées précédemment et que nous réunissons ici.

[1] m ( m – 1 ) ( m – 2) ( m – 3 ) …..( m – n + 1) arr^tg .

[2] 1 X 2 X 3 X 4 X 5 X…………………………………………..( n – 1) n .perm. soit l’écriture n! (lire n factoriel)

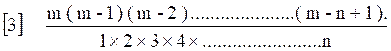comb.

le nombre des combinaisons s’obtient en divisant le nombre des arrangements par celui des permutations , c'est-à-dire que la formule générale des combinaisons de « m » objets groupés « n à n »

Nous allons les appliquer à des exemples.

PROBLEMES :

Problème n°1 :

De combien de manières différentes huit personnes peuvent-elles se placer autour d’une table ?

Cette question revient à demander quelles sont les permutations dont 8 objets (personnes) sont susceptibles. Il faut donc employer la formule (2) dans laquelle on remplacera « n » par 8, et elle donnera :

1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 = 40 320

Donc 8 personnes pourront dîner ensemble 40 320 fois pour épuiser toutes les positions diverses qu’elles peuvent prendre les unes relativement aux autres.

Problème n°2 :

Calculer le nombre des permutations qu’on peut faire avec 24 lettres ?

Dans ce cas , on fera avec « n » = 24 dans la formule ( 2) et elle deviendra :

1 X 2 X 3 X 4 X 5 X 6 X 7 X 8X…………………………………………..X 23 X 24 =

soit le calcul 24 ! ( lire : 24 factoriel)

En effectuant toutes les multiplication,on obtiendra, pour le nombre demandé : 620 448 401 733 239 439 360 000 permutations.

Commentaire sur ce nombre effrayant qui contient 620 sextillions, il faut se demander quelle étendue occuperaient ces permutations.

A cet effet, multiplions ce nombre par 24 pour avoir le nombre total des lettres contenues dans l’ensemble de toutes ces permutations ,et admettons que ces lettres , imprimées en caractères ordinaires,occupent chacune 4 millimètres carrés, ce qui fait 250 000 lettres par mètre carré.

Cela posé, on trouvera que toutes les permutations des 24 lettres de l’alphabet occuperaient une surface égale à 118 000 fois celle du globe terrestre.

Problème n°3 :

On a 90 numéros dans une urne , et l’on en tire 1 , ou 2 , ou 3 ou 4 , ou 5 ; ou 6 , quelle chance a-t-on que les numéros sortants soient ceux qu’on aurait désignés d’avance ?

Dans ce problème, on ne tient pas compte de l’ordre dans lequel se trouvent les numéros sortants ; en conséquence, la chance de demandée doit être calculée d’après le nombre des combinaisons de 90 numéros pris 1 à 1 ; 2 à 2 ; 3 à 3 ; 4 à 4 ; 5 à 5 , 6 à 6 ; c'est-à-dire qu’il faudra appliquer la formule (3 ) et prendre « m = 90 » et « n = 1 ; 2 ; 3 ; 4 ; 5 ; 6 » On aura donc. :

Pour 1 numéro ………………………………………………………………….. = 90 chances.

Pour 2 numéros ……………………………………………………………………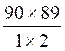 = 4005 chances

Pour 3 numéros………………………………………………………………….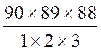 = 117 480 chances

Pour 4 numéros ………………………………………………………………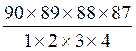. = 2 555 190 chances

Pour 5 numéros ………………………………………………………………….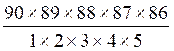 = 43 947 268 chances

Pour 6 numéros ……………………………………………………………………………………………………………………= ( à vous de calculer)

· Problème : le loto : On a 49 numéros dans une urne , et l’on en tire 1 , ou 2 , ou 3 ou 4 , ou 5 ; ou 6 , quelle chance a-t-on que les numéros sortants soient ceux qu’on aurait désignés d’avance ?

Problème n° 4 :

On doit loger 40 personnes dans deux dortoirs différents : le premier contient 33 lits , le second 7 lits ; de combien de manières peut-on distribuer ces 40 personnes. ?

Commentaire : l’ordre dans lequel seront placées les 33 ou les 7 personnes dans chaque chambrée n’étant pas en ligne de compte ,on doit chercher encore ici les combinaisons 7 à 7 ou 33 à 33 ; or , il faut observer que le nombre des unes , doit être égal à celui des autres , car chaque combinaison 7 à 7 en laisse nécessairement une 33 à 33.

D’ailleurs la formule (3) donne le même résultat , soit qu’on fasse « n = 7 » ou « n = 33 » ;

On a en effet ,

Pour « n=7 » , le nombre de manières = 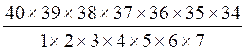= 18 643 560

Pour « n=33 » , le nombre de manières =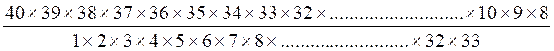

Et ces deux expressions sont égales , parce que dans la seconde il y a aux deux termes les facteurs communs 8X 9 X ………….X 32 X 33

Problème 5.

Au jeu de boston on donne 13 cartes sur 52 , combien de combinaisons différentes ?

La formule (3) donne 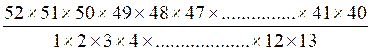= 635 013 559 600

Problème 6 :

Au jeu de piquet on a 32 cartes : On en donne 12 à chaque joueur ,et l’on laisse 8 cartes au talon ; on demande le nombre de combinaisons que peut offrir ce jeu.

La composition du jeu de chaque joueur est réglée par les combinaisons 12 à 12 des 32 cartes ; mais chacune d’elles doit se combiner ensuite avec les chances que donnent le jeu de l’autre joueur et les cartes du talon, c'est-à-dire avec les combinaisons 8 à 8 ou 12 à 12 des 20 cartes restantes , il faut donc multiplier ces deux résultats l’un par l’autre pour avoir les combinaissons demandées.

On posera donc :

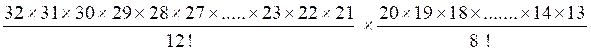
ce qui donne : 28 443 124 054 800 combinaisons.

Problème 7 :

Calculer le nombre de coups différents que l’on peut amener au jeu de dés :

1°) avec un dé

2°) avec deux dés ;

3°) avec trois dés,

etc.….. et en général avec « n » dés.

Info : Un dé est un petit cube dont les six faces sont numérotées de 1 à 6 par des points noirs, et la face qui reste en haut marque le coup.

Si l’on jette un seul dé,il est évident qu’on ne peut obtenir que six coups différents.

Si l’on prend deux dés, alors que chaque numéro de l’un peut se combiner avec les six numéros de l’autre, ce qui donnera 6 X 6 = 36 coups différents.

Avec trois dés , on verra que chaque face ou numéro du 3^ème pourra se combiner avec chacun des 36 coups fournis par les deux premiers,et qu’ainsi l’on aura 6 X 6 X6 = 216 coups différents, et ainsi de suite.

Donc, en général, le nombre de coups possibles est exprimé par le nombre 6 des faces de chaque dé , élevé à la puissance marquée par le nombre de dés employés.

Ainsi on aura

Avec 1 dé …………………………………..6 chances de sortir un ………………..1 ;2 ;3 ;……….6

Avec deux dés ………………………….6 ² chances de sortir un arrangement ……..

Avec 3 dés ………………………………6 ³ chances de sortir un arrangement……..

Etc…………………………………………………………………………

Avec « n » dés ………………………….6 ⁿ ……………………………. chances de sortir un arrangement……..

· Remarque : le jeu de dés offre une grande variété de chances,et donne lieu à un grand nombre de problèmes différents.

On peut se demander, par exemple, quelle est la probabilité que tous les dés marquent le même point.

Or ,quelque nombre de dés,qu’on jette, il n’y a qu’une manière d’avoir tous les as ; une pour tous les « 2 », une pour tous les « 3 » , etc., ce qui donne six chances seulement pour les coups égaux dans tous les cas ; ainsi c’est le calcul qui indique la probabilité demandée.

· En second lieu, demandons nous quelle est la probabilité d’amener trois points égaux avec quatre dés.

« m = 4 » et « n= 3 » ; combinaisons =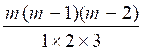

A cet effet, nous dirons : les quatre as,par exemple,dans ces quatre dés, peuvent donner 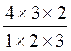= 4 combinaisons 3 à 3 ; il en sera de même pour obtenir 3 « deux » , 3 « trois » , 3 « quatre » , 3 « cinq », les 3 « six » donneront aussi 4 combinaisons chacun,ce qui fait en tout 24 combinaisons 3 à 3 ;

Mais pendant que trois dés marquent le même point, le 4^ème peut représenter tour à tour chacune des 5 autres faces, en sorte que les 24 combinaisons ci-dessus fourniront 24 X 5 = 120 combinaisons.,dans lesquelles trois dés marqueront le même point.

D’un autre côté , 4 dés pouvant donner 6 ⁴ = 1296 coups différents , on aura pour le rapport demandé :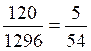

Problème XIII :

Etant donné un jeu de piquet ( 32 cartes) , calculer la chance que l’on a de tirer une quinte en prenant cinq cartes au hasard.

La quinte forme une des combinaisons 5 à 5 que peuvent donner les 8 cartes de chaque couleur qui entre dans un jeu de piquet, or, 8 cartes se combinent 5 à 5 de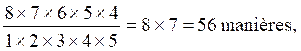

Ce qui fait pour les quatre couleurs : 56 X 4 = 224 combinaisons.

D’un autre côté, 32 cartes forment en tout 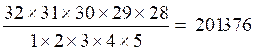combinaisons 5 à 5.

La chance demandée est donc de :

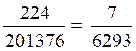
EXERCICES ET PROBLEMES. (sur la théorie des combinaisons)

1° ) De combien de manières 7 personnes peuvent-elles dîner ensemble en occupant toutes les places possibles ?

( réponse : 5040)

2°) Avec 100 soldats combien peut-on former de rangs de 5 hommes ?

( Réponse : 9 034 502 400)

3°) Sur un poste de 100 hommes , de combien de manières peut-on extraire une patrouille de 5 hommes. ?

( Réponse : 75 287 520)

4°) DE combien de manières peut-on distribuer 21 objets en 2 tas de 6 et de 15 ?

(Réponse : 54 264)

5°) Quelle chance a-t-on de tirer trois cartes désignées d’un jeu de 32 cartes. ?

(Réponse : 1 / 4960)

6°) On met 90 numéros dans un sac,et , après les avoirs bien agités, on les retire l’un après l’autre. Quelle est la probabilité que ces numéros sortirons dans l’ordre naturel de leur grandeur ?

(Réponse : le nombre total des permutations contre 1 )

7°) Au jeu de wist, ( ou de boston) quelle probabilité a – t-on que chaque joueur ait les 13 cartes de la même couleur ?

Ce problème revient à demander quel est le nombre total des combinaisons que peut offrir le jeu de wist ( ou de boston) relativement aux quatre joueurs.

Solution : Le jeu du premier joueur est réglé par les combinaisons données au problème n°5 ; celui du second dépend des combinaisons 13 à 13 des 39 cartes restantes ; enfin le 3^ème et le 4^ème joueur auront des jeux pris dans les combinaisons 13 à 13 des 26 autres cartes ; en sorte que la probabilité demandée dépend du produit de ces trois espèces de chances , et elle est exprimée par :

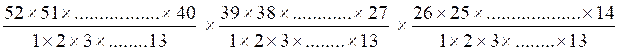
ce qui donne : 8 565 126 197 851 151 797 861 440 000

8°) Etant donnés les 73 caractères d’imprimerie qui compose les vers suivants.

Celui qui met un frein à la fureur des flots

Sait aussi des méchants arrêter les complots ;

On suppose que l’on jette les caractères sans ordre dans une boîte ; qu’après les avoir mêlés , on les en retire l’un après l’autre sans choix et qu’on les assemble au hasard ; quelle probabilité y a - t- il que ces deux vers ci-dessus soient reproduits ?

( Réponse : 73 X 72 X 71X ………………………3X 2 X 1 = 4,4701154615126843408912571381251 e+105 ) ce qui donne un nombre énorme !!!!!!!!!!!!!!

9°) On demande le nombre total des combinaisons 2 à 2 ; 3 à 3 ;etc.…. ;6 à 6 ;qu’on peut former avec les 7 couleurs primaire du spectre solaire .

TRAVAUX AUTO – FORMATIFS

CONTROLE:

- R

EVAL UATION: