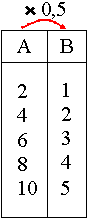|
WARMATHS |
Proportionnalité |
|
|
Définitions. |
|
|
|
|
Propriétés. |
|
|
|
|
Calculs de base. |
|
|
|
|
|
I) Calcul du coefficient de proportionnalité. |
|
|
|
|
II) Produits en croix. |
|
|
|
|
III) Quatrième proportionnelle. |
|
|
|
Comment reconnaître une situation de
proportionnalité? |
|
|
|
|
|
I) Tableau
de proportionnalité |
|
|
|
|
II) Droite dans un repère cartésien. |
|
|
|
|
|
|
|
|
Situations de proportionnalité. |
I) Pourcentages. |
|
|
|
|
II) Vitesses. |
|
|
|
|
« Vitesse moyenne » |
|
|
|
|
III )Echelles. |
|
|
|
|
|
Généralités. |
|
|
|
|
Comparaison d'échelles. |
|
|
|
|
|
Une suite de nombres est un ensemble de nombres entiers ou non, relatifs ou non. Le rang qu'occupe un nombre dans une suite est importante. Exemple: (2; -5; 4.5; 1/3; -1.02) est différente de (2; -5; 1/3 4.5; -1.02) parce que deux nombres ont échangé leur place.
Les suites de nombres A et B sont proportionnelles lorsque tout nombre de l'une est obtenu en multipliant le nombre de même rang de l'autre, par un même nombre appelé coefficient de proportionnalité.
Exemple: A=(9;5;-1;6) et B=(27;15;-3;18) sont proportionnelles . Tout nombre de B est obtenu en multipliant un nombre de A par 3. Le coefficient de proportionnalité de A vers B est donc 3. Nous obtenons les nombres de A en multipliant les nombres de B par 1/3. Le coefficient de proportionnalité de B vers A est donc 1/3.
Remarque:
- Les nombres, dans la suite, sont séparés par des points-virgules (;). Ce qui prévient les erreurs en cas d'utilisation de nombres à virgule.
- Ces deux coefficients sont « inverses » l'un de l'autre (le nombre non nul x a pour inverse 1/x: le produit x.1/x est égal à 1. Zéro n'a pas d'inverse). Par conséquent: l'inverse de 3 est 1/3 et 9*3=27 et 27*1/3=9 (nous avons fait un "aller-retour"). Vous retiendrez que:
Si k est le coefficient de proportionnalité de A vers B
Alors le coefficient de proportionnalité de B vers A est 1/k, inverse de k.
Représentation: Deux suites proportionnelles sont
souvent représentées par des tableaux horizontaux ou verticaux ainsi que dans
un repère du plan:
|
Horizontal |
Vertical |
Repère du plan |
||||||||||||||||||||
|
|
|
Nous pouvons changer un nombre de place dans l'une des suites proportionnelles à condition de changer de la même façon la place des nombres correspondants dans les autres suites.
Si A et B sont deux suites proportionnelles
alors la somme de deux ou plusieurs nombres de B est
proportionnelle à la somme des nombres correspondants de A.
|
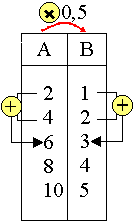
Exemple: Dans les suites proportionnelles ci-contre, 1 et 2 de B sont proportionnels à 2 et 4 de A. Dans B la somme de 1 et 2 est 3 qui est proportionnel à la somme de 2 et 4 (=6) dans A: (2+4)*0,5=2*0,5+4*0,5=1+2=3 et 2+4=6 qui est proportionnel à 6*0,5=3. Vérifiez avec 2+6, 4+6, 2+8 de A mais aussi avec des différences: 8-6, 10-4, 10-6 de A |
|
Si A et B sont deux suites proportionnelles
alors le produit d'un
nombre de A par un nombre x est proportionnel au produit du nombre
correspondant de B par x.
|
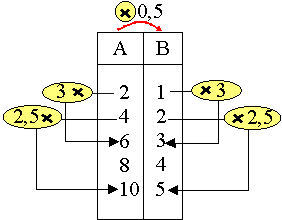
Exemple: Dans les suites proportionnelles ci-contre, en multipliant 2 par 3 dans la suite A et en multipliant le nombre 1 proportionnel à 2 dans B par la même valeur 3. Dans B nous obtenons 3 qui est proportionnel à 6 (2fois3) dans A. De même en multipliant 2 dans B , proportionnel à 4 dans A, par la valeur 2,5 nous obtenons 5 qui est proportionnel à 10 dans A (obtenu en multipliant 4 par 2,5 dans A) |
|
Dans un repère du plan: Si deux suites A et B sont proportionnelles
Alors les
points représentant les couples de nombres de A et B sont alignés sur une
droite passant par l'origine du repère.
|
|
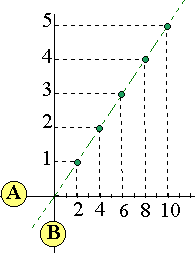
Les suites A et B sont proportionnelles. Le repère orthogonal ci-contre a des axes gradués avec des unités différentes, ce qui n'a aucune importance pour la propriété étudiée ici. Nous avons placé les nombres de A sur l'axe des abscisses et ceux de B sur l'axe des ordonnées. Les traits en pointillés montrent comment la relation s'établit entre deux nombres de même rang de chaque suite. Ces traits sont parallèles aux axes. Leurs intersections déterminent ainsi des points alignés sur une droite passant par l'origine du repère situé à l'intersection des axes. |
|
Remarque: La droite n'est pas tracée en trait fort car cela signifierait que tous ses points représentent un couple de nombres pris dans les suites A et B. Ce qui n'est pas le cas ici: il n'y a que 5 nombres dans chaque suite et donc, 5 couples à représenter (par 5 points).
I ) Calcul du coefficient de proportionnalité:
Pour calculer le coefficient de proportionnalité de deux suites proportionnelles A et B il suffit de connaître des nombres de chaque suite et de même rang.
Exemple: A et B sont proportionnelles telles que A=(5; 12; z; 10; 7) et B=(x; 7,2; 1,8; y; 4,2) où nous connaissons 12 et 7,2 de même rang. Le coefficient de proportionnalité de A vers B se calcule en divisant un nombre de B par celui qui lui correspond dans A c'est à dire 7,2/12=0,6 .
Vérifiez en prenant un nombre de A et en multipliant par 0,6: 5*0,6=3 (donc x=3) 12*0,6=7,2 (c'est bien ce qui est donné) 10*0,6=6=y et 7*0,6=4,2 qui est connu.
Pour calculer z il faut utiliser le coefficient de B vers A. Nous savons que ce coefficient est l'inverse du coefficient de A vers B: inverse de 0,6 est 1/0,6 ou 10/6 (fraction décimale: pour l'obtenir, multipliez le numérateur et le dénominateur par 10). Donc z=1,8*10/6=18/6=3.
Remarque: Nous pouvions aussi calculer le coefficient de proportionnalité de B vers A en divisant un nombre de A par le nombre de même rang dans B.
|
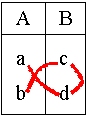
Soient les suites proportionnelles A= (a;b) et B(c;d). Nous avons l'égalité suivante: ad = cb |
|
Exemple d'utilisation: Soient les suites proportionnelles A=(5; 4; y) et B=(12,5; x; 10). Calculer x et y.
|
Nous écrivons le produit en croix pour les deux premières lignes du tableau: 5 x
= ( 12,5) (4) 5x = 50 ( 5x ) :
50 = 50 : 50 (R2) (voir Equations) x=10 De même pour la première et la dernière ligne: 5 fois 10 =12,5 y Nous trouvons y = 4. |
Remarque: Ce produit en croix a des applications importantes dans les calculs avec des cosinus ou des égalités de quotients (quotients égaux).
|
Si les nombres 4, 20, 7 et x , dans cet ordre, constituent un tableau de proportionnalité (voir ci-contre) alors le quatrième nombre est appelé quatrième proportionnelle. |
Pour calculer cette quatrième proportionnelle il suffit d'utiliser soit le coefficient de proportionnalité (après l'avoir calculé) ou les produits en croix (ce qui est plus élégant):
|
coefficient de proportionnalité=20/4=5 d'où x= (7 ) (5 )=35. |
Produits en croix: (4) (x) = (20) (7) (4 x) : 4= (140 ) : 4 d'où x =35 |
La quatrième proportionnelle à 4, 20 et 7 est 35
|
Comment reconnaître une situation de proportionnalité ?
|
Info +++@ |
Une situation de proportionnalité est traduite par deux suites ... proportionnelles. Pour vérifier que deux suites inconnues sont proportionnelles, vous pouvez:
Les mettre sous forme de tableau: et
- mettre en évidence un coefficient de proportionnalité (en le calculant pour chaque couple de nombres des suites). Exemple:
|
4:16=0,25 6:14=0,25 2:8=0,25 Le coefficient de proportionnalité est 0,25. A et B sont proportionnelles |
ou
- effectuer le produit en croix plusieurs fois si cela est nécessaire.
|
( 2,3 ) (34 ) =78,2 et (1,7) (46) =78.2 (1,7) ( 9 )= 15,3 et (0,45 ) ( 34 )=15,3 Les suites A et B sont proportionnelles. Remarques: - Il est inutile de vérifier 1ère ligne avec dernière ligne. - Les produits en croix sont égaux pour deux lignes mais différents lorsque nous changeons de paire de lignes |
Remarque: Il est bien évident que si nous trouvons une différence sur le coefficient ou dans un produit (aussi petite soit-elle) nous concluons que les suites ne sont pas proportionnelles.
Les représenter dans un repère du plan:
|
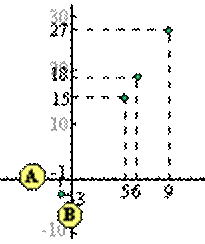
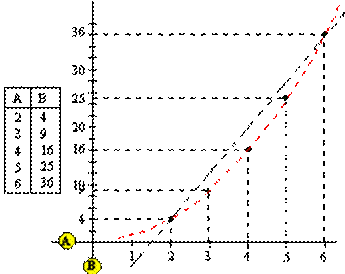
Représenter les couples de nombres des deux suites (la méthode ne concerne que deux suites) par des points dans un repère. Puis vérifier que ces points sont bien alignés sur une droite passant par l'origine du repère. Si ils le sont alors les deux suites données sont proportionnelles (si un seul de ces points n'est pas aligné avec les autres ou si la droite ne passe pas par l'origine du repère, alors les deux suites ne sont pas proportionnelles). Dans l'exemple ci-contre, les suites A et B ne sont pas proportionnelles (points non alignés). |
|
Situations de proportionnalité:
Généralités et définitions:
Dans la presse nous pouvons très souvent lire les résultats de sondages d'opinion. Du genre: "60% des enfants de moins de 6 ans préfèrent la couleur rouge". Est ce à dire que l'organisme qui a calculé ce résultat, a interrogé TOUS les enfants de moins de 6 ans de la population concernée? Sûrement pas! Cet organisme a sélectionné un échantillon (une toute petite partie de la population: 1000 enfants de moins de 6 ans par exemple), a interrogé ces enfants et a trouvé 600.
L'organisme de sondage utilise une méthode qui lui permet d'affirmer que si il avait interrogé 10000 enfants il aurait trouvé 10 fois plus d'enfants préférant la couleur rouge, c'est à dire 6000. Le résultat, au lieu de 600 pour 1000, serait 6000 pour 10000 mais exprimerait la même réalité.
Nous avons deux suites proportionnelles:
-les échantillons possibles: (1000; 10000)
-les enfants préférant la couleur rouge: (600; 6000)
Le coefficient est 600:1000=0,6.
Que signifie 60% ? C'est une notation rapide pour écrire 60 pour 100 c'est à dire 60/100=0,6.
60% est appelé pourcentage. C'est un coefficient de proportionnalité entre une suite d'échantillons et une suite de résultats obtenus par étude.
Les échantillons peuvent être de diverses sortes: populations, récoltes de légumes, production de matières premières, métaux, sommes d'argent,... De même pour les études conduites sur ces échantillons: mesures diverses (pesées,..), comptages,..
Exemples:
Ex 1: Un morceau de minerai arraché à la montagne pèse 200g et contient 0,1g d'or. Quel pourcentage d'or pur contient ce minerai?
L'échantillon pèse 200g. Nous estimons que la quantité d'or contenu dans le minerai est proportionnelle à la masse du morceau de minerai. Si nous en prenons la moitié (100g) nous obtiendrons la moitié d'or soit 0,05g. C'est à dire 0,05 pour 100 ou 0,05%. Nous aurions pu utiliser un tableau:
|
Calcul de x en utilisant le produit en croix: 200 x = (0,1 ) (100 ) 200 x : 200= (10) (1/200) x = 0,05 |
Remarques:
- Pour calculer un pourcentage il suffit de placer dans le tableau 100 unités de l'échantillon (l'unité ici est le gramme) et de poser x comme résultat de l'étude.
- La notation (R2) concerne une règle de calcul dans la résolution des équations.
Ex 2: Un commerçant vend des chemises. Pendant les semaines de soldes, tous ses articles subissent un rabais de 15%. Combien est vendue une chemise coûtant initialement 420€.
|
Remise= (420 ) (0,15) =63 Prix soldé= 420-63=357 La chemise est vendue 357 € , pendant la première semaine. |
||||||
Remarque: Pour un objet coûtant 100€ la remise est 15€ (ce que signifie 15% de soldes), le prix après remise est donc 100-15= 85 €. Nous pouvons affirmer que le prix soldé est 85% du prix initial (85€ des 100€ avant remise). Le calcul du prix de la chemise est alors direct: 420 x 0,85= 357 (0,85=85/100)
Généralités et Unités:
Un objet n'est mobile (bouge...) que par rapport à un autre. Deux objets A et B peuvent être mobiles par rapport à un troisième objet C mais immobiles par rapport l'un à l'autre. Exemple deux pilotes d'un avion en vol sont immobiles l'un par rapport à l'autre alors qu'ils se déplacent par rapport au sol.
La façon de se déplacer d'un mobile peut être variable: accélération suivi de ralentissements, d'arrêts...
Pour rendre compte du mouvement d'un mobile nous utilisons la notion de vitesse: distance dont se déplace le mobile pendant une durée choisie comme unité. Si cette distance est toujours la même, pour un mobile donné, alors son mouvement est uniforme.
Le nombre qui exprime cette vitesse change en fonction des unités choisies:
|
Unités de
distances |
Unités de durée |
Vitesse |
|
Kilomètre (km) |
Heure (h) |
Kilomètre par heure
( km.h) |
|
Mètre (m) |
Seconde (s) |
Mètre par seconde (m.s) |
|
Kilomètre (km) |
Seconde (s)
|
Kilomètre par
seconde (km.s) |
|
Kilomètre (km) |
Minute (mn) |
Kilomètre par minute
(km.mn) |
|
... |
... |
... |
La même vitesse peut donc s'exprimer avec des nombres différents: 6 km.h = 6000 m.h = 100 m.mn. Pour cette dernière égalité il suffit de bien comprendre 6000 m.h : 6000 m en une heure, combien en une minute? La réponse: 60 fois moins (car il y a 60mn dans une heure) donc 6000:60=100. Nous trouvons donc 100 m.mn (100 mètres par minute).
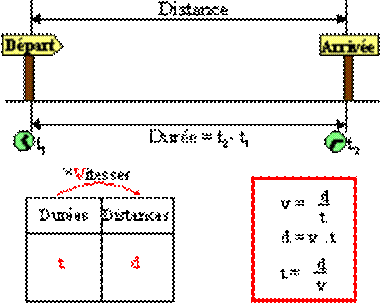
Nous ne nous intéresserons pas ici à la vitesse réelle d'un mobile (il faudrait le suivre instant par instant pour avoir les vitesses à ces instants, appelées vitesses instantanées, qui changent sans cesse sauf pour le mobile animé d'un mouvement uniforme). Nous ne prendrons en compte que la durée entre deux instants (instant de départ et instant d'arrivée par exemple) et la distance parcourue pendant cette durée. Les variations de mouvement qui ont pu survenir entre les deux instants sont négligées. La vitesse calculée à l'aide de ces deux données est appelée vitesse moyenne.
|
Dans ce cas la distance parcourue est proportionnelle à la durée mise à la
parcourir. Le coefficient de proportionnalité entre la suite des distances et
la suite des durées est la vitesse moyenne. Pour calculer cette vitesse nous calculons un coefficient de proportionnalité: Vitesse=Distance: durée ou v = ou « t » exprime la durée (ce qui évite d'utiliser les deux mêmes lettres dans la même formule!
|
|
Remarques importantes:
- Si nous connaissons la durée et la vitesse, nous sommes alors capables de calculer la distance parcourue: la suite des durées T multipliée par le coefficient de proportionnalité vitesse V donne la suite des distances D. Ce qui est exprimé par la deuxième formule ci-dessus: d=vt.
- Si nous connaissons la suite des distances D et la vitesse V, nous sommes capables de calculer la suite des durées T: la suite des distances D multipliée par le coefficient de D vers T (qui est l'inverse du coefficient de T vers D, c'est à dire inverse de la vitesse) donne la suite des durées T. Ce qui se traduit par la troisième formule ci-dessus: t= ( d ) (1/v) ou t = d /v (1/v est l'inverse de v).
- La durée est souvent calculée en faisant une différences d'instants donnés. Exemple: départ à t1=9h20mn et arrivée à t2=12h. La durée t est t=t2- t1=12h-9h20mn soit t=2h40mn (voir Conversions pour ce type de calculs et des exemples de calculs de vitesses)
Exemple:Dans une vallée, j'entends l'écho de ma voix 4 secondes après avoir parlé. A quelle distance de moi se trouve l'écran qui réfléchit ma voix?
Remarque: Le son se déplace à une vitesse de 340m.s. Le son ne contourne pas les obstacles, il les pénètre (si cela lui est possible: parois minces et peu denses par exemple) ou il "rebondit" dessus (paroi très dense par exemple). C'est le phénomène de l'écho.
En 4s le son parcourt: 340*4=1360m. Cette distance représente un "aller-retour". L'écran qui réfléchit ma voix se trouve donc à 1360:2=680m.
Généralités et définitions:
Pour représenter la réalité sur une feuille de papier il nous faut la dessiner. Si nous désirons un plan exact d'un objet nous sommes obligés de dessiner cet objet sans le déformer.
|
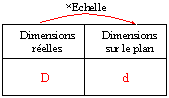
Pour cela les dimensions (longueurs, largeurs, hauteurs, épaisseurs ou profondeurs) du dessin doivent être proportionnelles aux dimensions de l'objet dans la réalité. Le coefficient de proportionnalité (réalité vers dessin) est appelé échelle (notée :e ) du dessin (ou du plan). |
|
L’échelle est égale au rapport de la dimension du plan sur la dimension réelle.
Nous avons donc les formules suivantes (qui sont semblables aux formules sur les vitesses et sur les pourcentages):
d = D.e
e = d / D
et
D = d / e
Remarques:
- Attention aux unités employées. Les dimensions réelles sont souvent très différentes des dimensions sur le dessin. Par exemple les dimensions d'une maison s'expriment en mètres et nous utilisons un double décamètre pour les mesurer. Sur le dessin nous utiliserons un double décimètre... Mais nous noterons les dimensions (cotations du dessin) avec leurs valeurs réelles.
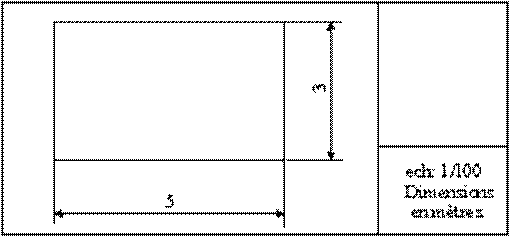
Pour éviter les erreurs, avant tout calcul, nous convertirons toutes les mesures (dans la réalité et sur le dessin) dans la même unité (le centimètre par exemple).
- Les échelles sont souvent données sous forme de fractions dont le numérateur est 1 (1/10; 1/100; 1/2500;...). Ceci est très pratique: 1/100 signifie que 1 unité sur le dessin en représente 100 dans la réalité (par exemple: 1cm sur le dessin représente 100cm dans la réalité).
- Un objet représenté en grandeur réelle est dessiné à l'échelle 1.
- Nous utilisons une échelle inférieure à 1 pour dessiner ce qui est trop grand (impossible de dessiner l'objet en grandeur réelle sur notre feuille de papier) et une échelle supérieure à 1 pour dessiner ce qui est trop petit (impossible de représenter correctement les détails de l'objet).
Exemple de calculs:
|
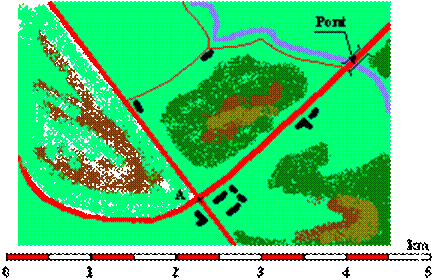
Sur une carte routière (voir extrait ci-contre) l'échelle est indiquée par un segment gradué de 0 à 5 mesurant 10cm. L'unité indiquée sur ce segment est le kilomètre. Nous voudrions connaître la distance réelle entre le carrefour A et le Pont. Nous avons relevé sur la carte une distance de 4,8cm. Quelle est la distance réelle?
|
|
Deux méthodes s'offrent à nous:
- Méthode graphique: prendre la mesure entre le carrefour et le pont avec un compas. Reporter cette mesure sur l'échelle à partir du 0. Lire sur la graduation du segment la distance cherchée: 2,4km.
- Par le calcul:
|
Il nous faut connaître l'échelle de cette carte: 10cm représentent 5km ou 500000cm. L'échelle est donc 10 pour 500000 ou 10/500000 soit 1/50000. x*1/50000=4,8 x*1/50000*50000=4,8*50000 x=240000 La distance recherchée est donc 240000cm ou 2,4km. |
Remarque: Nous pouvons trouver x sans calculer l'échelle: en utilisant les produits en croix.
500000*4,8=10*x...
Comparaison d'échelles:
Une échelle de 1/100 est utilisée pour des plans plus détaillés que ceux réalisés avec une échelle de 1/1000. En effet 1 unité représente 100 unités dans le premier cas, et 1000 unités dans le second: sur un même espace nous avons représenté une plus petite partie de la réalité dans le premier cas, les détails sont donc plus grands. Le dessin est plus lisible avec une échelle plus petite.
Exemple:
|
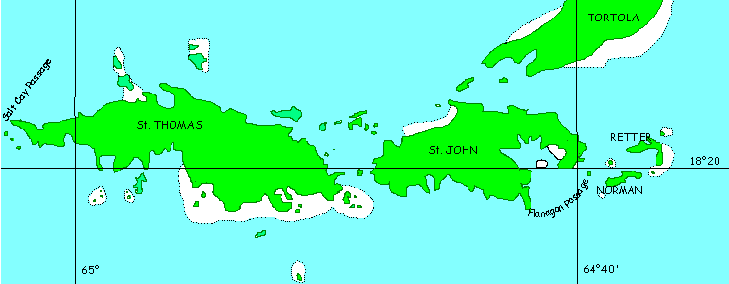
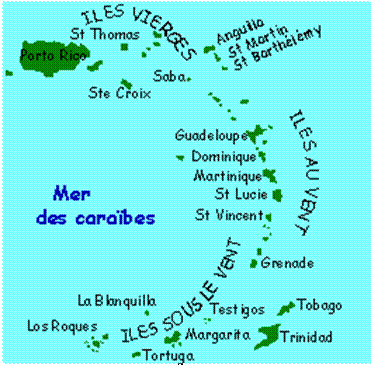
Un navigateur désirant faire une croisière dans les Caraïbes (situées dans le golfe du Mexique en Amérique du Nord) doit se munir d'une carte maritime à grande échelle (extrait de carte ci-contre). Sur une telle carte les îles les plus petites sont représentées par un point. |
|
Si ce navigateur désire se rendre dans quelques unes de ces petites îles, il doit se munir en outre de cartes à plus petites échelles afin d'obtenir les détails nécessaires à sa navigation (formes des côtes, passage entre deux îles, mouillages,...). L'extrait de carte ci-dessous, à plus petite échelle, montre plus de détails sur quelques unes des îles Vierges indiquées sur la carte ci-dessus.